Grupa: Porovnání verzí
m sjednoceni <- Abelova grupa |
m →Symetrie v krystalografii: zkraceni |
||
| Řádek 604: | Řádek 604: | ||
| rok=2006 |
| rok=2006 |
||
| isbn= 0-521-82212-2 |
| isbn= 0-521-82212-2 |
||
| jazyk=anglicky}}</ref><ref> {{Citation | last1 = Jahn | first1=H.| author1-link=Hermann Arthur Jahn|last2=Teller|first2=E.|author2-link=Edward Teller| title = Stability of Polyatomic Molecules in Degenerate Electronic States. I. Orbital Degeneracy | year = 1937 | journal = [[Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences (1934–1990)]] | volume = 161 | issue = 905 | pages = 220–235 | doi = 10.1098/rspa.1937.0142}}</ref> |
| jazyk=anglicky}}</ref><ref> {{Citation | last1 = Jahn | first1=H.| author1-link=Hermann Arthur Jahn|last2=Teller|first2=E.|author2-link=Edward Teller| title = Stability of Polyatomic Molecules in Degenerate Electronic States. I. Orbital Degeneracy | year = 1937 | journal = [[Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences (1934–1990)]] | volume = 161 | issue = 905 | pages = 220–235 | doi = 10.1098/rspa.1937.0142}}</ref> Podobně, teorie grupa může být použita pro popis změn fyzikálních vlastností, které se dějou u [[fázový přechod|fázového přechodu]], například při změně typu [[Krystalová mřížka|mřížky]].<ref name="pozn"> |
||
Analogické spontánní [[narušení symetrie]] se využívá v [[kvantová teorie pole|kvantové teorii pole]] k teoretickému vysvětlení vzájemných interakcí [[částice|částic]], např. v teorii [[elektroslabá interakce|elektroslabé interakce]], viz např {{Citace monografie |
|||
| ⚫ | |||
Podobně, teorie grupa může být použita pro popis změn fyzikálních vlastností, které se dějou u [[fázový přechod|fázového přechodu]], například z kubické do tetrahedrální mřížky. Příklad je [[feroelektrický]] materiál, kde změna od [[paraelektrický|paraelektrického]] k feroelektrickému stavu nastává u [[Curieho teplota|Curieho teplotě]] a je spojena se změnou od vysoké symetrie paraelektrického stavu k nižší symetrii feroelektrického stavu. Tuto změnu doprovádí měkký [[fonon]]ový mód, mód vibrační mřížky jehož frekvence se v přechodu blíží nule.<ref>{{Citace monografie |
|||
| ⚫ | |||
| ⚫ | |||
| titul=Electroweak Symmetry Breaking: The Bottom-Up Approach |
|||
| ⚫ | |||
| vydavatel=Springer |
|||
| titul=Structure and Dynamics: an atomic view of materials |
|||
| vydavatel=Oxford University Press |
|||
| strany=265 |
|||
| rok=2003 |
| rok=2003 |
||
| isbn= |
| isbn= 9780387400976 |
||
| jazyk=anglicky}}</ref> |
|||
| jazyk=anglicky}}</ref> Toto spontánní [[narušení symetrie]] má aplikace v [[částicová fyzika|částicové fyzice]]. Jeho výskyt je spojen s existencí tzv. [[Goldstonův bozon|Goldstonova bozonu]]. |
|||
{| class="wikitable" border="1" style="text-align:center; margin:1em auto 1em auto;" |
{| class="wikitable" border="1" style="text-align:center; margin:1em auto 1em auto;" |
||
Verze z 16. 6. 2011, 00:49

Grupa je v matematice algebraická struktura, která popisuje a formalizuje koncept symetrie. Formálně se zavádí jako množina spolu s binární operací splňující níže uvedené axiomy. Matematická disciplína zabývající se studiem grup se nazývá teorie grup.
Teorie grup vznikla počátkem 19. století. U jejího zrodu stál matematik Évariste Galois, který dokázal, že polynomiální rovnice nelze obecně řešit pomocí odmocnin. Grupy našly později uplatnění také v geometrii, teorii čísel, algebraické topologii a dalších matematických oborech. Klasifikace jednoduchých konečných grup byla dokončena koncem 20. století a patří k největším výsledkům matematiky vůbec.
Pojem grupy abstraktně popisuje či zobecňuje mnoho matematických objektů a má významné uplatnění i v příbuzných oborech – ve fyzice, informatice a chemii. Reprezentace grup hrají důležitou úlohu v teoriích jako jsou částicová fyzika, kvantová teorie pole anebo teorie strun. V informatice se grupy vyskytují například v kryptografii, kódování anebo zpracování obrazů, chemie používá grupy pro popis symetrií molekul a krystalových mřížek v krystalografii.
Příklady grup jsou celá čísla se sčítáním, racionální čísla bez nuly s násobením, symetrie pravidelných geometrických útvarů, množiny regulárních matic a automorfismy různých algebraických struktur.
Definice grupy
Grupou nazýváme množinu spolu s binární operací na ní, která se nazývá grupová operace. Tato operace vezme dva prvky grupy a výsledek je jeden prvek grupy , resp. jenom . Podle kontextu říkáme, že je složení, resp. součin, resp. součet prvků a . Dále se v definici grupy požaduje, aby operace splňovala určité vlastnosti, které se nazývají axiomy grupy.[1]
Pro všechny prvky v je i součin také prvkem . [2]
Pro všechny prvky grupy platí , t.j. výsledek složení více než dvou prvků nezávisí na ozávorkování.
Existence neutrálního prvku
Existuje prvek takový, že pro všechna platí . Tento prvek se nazývá neutrální prvek anebo jednotkový prvek a značí se také , resp. .[2]
Existence inverzních prvků
Pro každý prvek grupy existuje prvek takový, že , t.j. jejich složení v libovolném pořadí je rovno neutrálnímu prvku . Prvek se také nazývá inverzní prvek k a značí se . Lze ukázat, že neutrální prvek je v grupě jenom jeden a že inverzní prvek k je dán jednoznačně.
Množina z této definice se označuje jako nosič nebo nosná množina grupy. Označíme-li operaci jako sčítání , mluvíme o aditivní grupě a píšeme . Obvykle se používá aditivní notace pro grupy Abelovy a neutrální prvek se pak zapisuje jako . Označíme-li operaci jako násobení , hovoříme o multiplikativní grupě a píšeme . V takovém případě se často znak nepíše a součin prvků se značí jako . Neutrální prvek multiplikativní grupy se obvykle značí jako .
Ekvivalentně lze grupu definovat pomocí
- nulární operace (tj. konstanty) představující neutrální prvek,
- unární operace -1, která každému prvku přiřadí prvek k němu inverzní, a
- binární operace.
Místo označení "grupa " se pak používá označení "grupa ". Výše uvedené axiomy lze pak přepsat do výroků, které neobsahují existenční kvantifikátory. Třída všech grup proto tvoří varietu[3] a tak lze na grupy vztáhnout mnohé výsledky dokázané v univerzální algebře.
Ilustrativní příklady
Celá čísla
Jedním z nejjednodušších příkladů grupy je množina celých čísel spolu s operací sčítání.[4][5]
- Operace sčítání je na této množině binární operace, protože součtem dvou celých čísel je opět celé číslo.
- Sčítání je asociativní,
- Nula je neutrální prvek, protože pro každé celé číslo a platí
- Pro každé celé číslo a existuje opačné číslo -a, .
Axiomy jsou tedy splněny. Tato grupa se obvyle značí .
Dihedrální grupa D4
Symetrie čtverce jsou definovány jako rotace, zrcadlení resp. jejich složení, které převádí čtverec sám na sebe. Množina všech takových symetrií tvoří grupu, která má osm prvků a značí se D4.[5][6] Následuje popis těchto symetrií:
| • | id | r1 | r2 | r3 | fv | fh | fd | fc |
|---|---|---|---|---|---|---|---|---|
| id | id | r1 | r2 | r3 | fv | fh | fd | fc |
| r1 | r1 | r2 | r3 | id | fc | fd | fv | fh |
| r2 | r2 | r3 | id | r1 | fh | fv | fc | fd |
| r3 | r3 | id | r1 | r2 | fd | fc | fh | fv |
| fv | fv | fd | fh | fc | id | r2 | r1 | r3 |
| fh | fh | fc | fv | fd | r2 | id | r3 | r1 |
| fd | fd | fh | fc | fv | r3 | r1 | id | r2 |
| fc | fc | fv | fd | fh | r1 | r3 | r2 | id |
| Prvky id, r1, r2 a r3 tvoří podgrupu, zvýrazněnou červeně (levá horní oblast). Prvek levé a pravé třídy rozkladu podle této podgrupy je zvýrazněna zelenou (v posledním řádku) a žlutou (v posledním sloupci). | ||||||||
- Identita (id) nechává čtverec nezměněn
- Rotace čtverce o 90°, 180°, a 270° doprava (r1, r2 and r3)
- Překlopení (také reflexe nebo zrcadlení) kolem vetrikální a horizontální střední úsečky (fh and fv), a kolem dvou diagonál (fd and fc).
Binární operaci v této grupě definujeme jako skládání zobrazení: osm symetrií jsou zobrazení ze čtverce na čtverec a dvě symetrie se dají složit do nové symetrie. Je zřejmé, že výsledek bude opět symetrie čtverce. Výsledek operace "nejdříve a a pak b" se obvykle značí zprava doleva jako b∘a. Stejné značení se totiž používá pro skládání zobrazení. Například r_1∘r_1=r_2.
Tabulka vpravo znázorňuje výsledky všech možných složení. Například výsledek složení rotace o 270° doprava (r3) a horizontálního překlopení (fh) je stejný jako překlopení kolem diagonály (fd). Formálně,
což je v tabulce zvýrazněno modrou barvou. Vidíme také, že grupa není komutativní, neboť například
Dějiny

Koncept grupy se vyvinul z různých oblastí matematiky.[7][8][9] Původní motivace pro teorii grup byla snaha řešit polynomiální rovnice stupně vyššího než 4. Kvadratické rovnice uměli lidé řešit už v starověkých civilizacích.[10] Lodovico Ferrari uměl řešit polynomiální rovnice stupně 3 a 4 kolem roku 1540,[11] řešení publikoval spolu s Gerolamo Cardanem v knize Ars Magna v roce 1545. Polynomiální rovnice vyššího stupně však obecně nelze řešit pomocí odmocnin. Počátkem 19. století francouzský matematik Évariste Galois, navazujíc na starší práce Ruffiniho a Lagrangeho naleznul kritérium pro řešitelnost polynomiálních rovnic pomocí radikálů. Existence takového řešení závisí na grupě symetrií kořenů daného polynomu. Tato grupa se dnes nazývá Galoisova grupa a její prvky jsou jisté permutace kořenů.
Galoisovy myšlenky byly původně odmítnuty jeho současníky a publikovány až posmrtně.[12][13] Obecnější permutační grupy byly zkoumány Augustinem Cauchym. První definici konečné grupy a také název "grupa" zavedl Arthur Cayley v publikaci On the theory of groups, as depending on the symbolic equation θn = 1 (1854).
Geometrie byla druhou oblastí, v které byly grupy systematicky využívány, hlavně grupy symetrií geometrických prostorů zavedené Felixem Kleinem v Erlangenském programu v roce 1872.[14] Klein využil teorii grup pro popis a kategorizaci nově se objevyvších geometrií jako hyperbolická geometrie, projektivní geometrie a starší Eukleidova geometrie. Dále tento koncept rozvinul Sophus Lie, který zavedl pojem a studium Lieových grup v roce 1884.[15]
Třetí oblast, která přispěla ke vzniku a rozšíření teorie grup byla teorie čísel. Jisté struktury odpovídající Abelovým grupám byly implicitně použity v Gaussově číselně teoretickém díle Disquisitiones Arithmeticae a explicitněji je používal i Leopold Kronecker.[16] V roce 1847, Ernst Kummer v raných pokusech dokázat Velkou Fermatovu větu zavedl grupy popisující faktorizaci na prvočísla.[17]
Spojování těchto různých motivů do jednotné teorie grup začalo Jordanovou publikací Traité des substitutions et des équations algébriques (1870).[18] Walther von Dyck (1882) zavedl první moderní definici grupy.[19]
Počátkem 20. století získaly grupy široké přijetí díky práci Ferdinanda Frobenia a Williama Burnsidea, kteří pracovali na teorii reprezentací konečných grup a také díky článkům Richarda Brauera (modulární teorie reprezentací) a Issaie Schura.[20] Teorie Lieových grup, a obecněji lokálně kompaktních grup byla publikována Hermannem Weylem, Élie Cartanem a mnoha dalšíma.[21] Její algebraický protějšek, teorie algebraických grup, byla prvně popsána Chevalleyem (koncem 30. let) a později Armandem Borelem a Jacquesem Titsem.[22]
V rocích 1960-61 zorganizovala Univerzita v Chicagu Rok teorie grup a teoretici jako Daniel Gorenstein, John G. Thompson a Walter Feit založili spolupráci která, s přispěním mnohých jiných matematiků, vedla ke klasifikaci jednoduchých konečných grup v roce 1982. Tento projekt předčil předchozí matematická úsilí svým rozsahem a to jak délkou důkazů, tak počtem zainteresovaných matematiků. Ačkoliv je klasifikace hotova, výzkum pokračuje s cílem zjednodušit důkaz této klasifikace.[23] V současnosti je teorie grup pořád se rozvíjející oblast matematiky, která má vliv na mnoho souvisejících teorií.
Základní grupové pojmy
V této kapitole budeme značit grupu multiplikativně, t.j. binární operace bude • a součin prvků a a b budeme značit a•b, anebo a+b pro Abelovy grupy.
Řád prvku a grupy
Řádem grupy se nazývá mohutnost |G| její nosné množiny.
Řádem prvku g se nazývá nejmenší přirozené číslo n takové, že gn=g•g• ... •g=e (součin n krár prvku g) anebo ∞, pokud takové neexistuje.[24]
Cyklická grupa
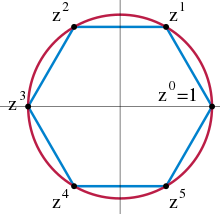
- Hlavní článek: Cyklická grupa
Grupa G se nazývá cyklická, pokud je generována jedným prvkem. To znamená, že existuje prvek x∈G takový, že každý prvek g ∈ G lze napsat jako xn pro nějaké celé číslo n.[25] xn=x•x• ... •x znamená, že prvek x je vynásoben sám se sebou n krát, a x-n=x-1•x-1•...•x-1 znamená, že je prvek x-1 vynásoben sám se sebou n krát pro nějaké přirozené číslo n. Konečnou cyklickou grupu řádu n lze reprezentovat množinou řešení rovnice zn=1 v komplexní rovině, což je pro n=6 znázorněno na obrázku vpravo. Grupové násobení je pak obyčejné násobení komplexních čísel. Jinou reprezentaci představuje množina zbytkových tříd spolu se sčítáním modulo n.
Pokud je cyklická grupa nekonečná, je izomorfní grupě celých čísel . Pokud je konečná a má n prvků, je izomorfní množině zbytkových tříd .[26]
Abelova grupa
Grupu nazýváme Abelovou (také komutativní či Abelovou), platí-li pro všechna a, b ∈ G. Pojmenování je po norském matematikovi Henrikovi Abelovi.[27] Příklady Abelových grup grup jsou celá čísla spolu s operací sčítání , reálna čísla se sčítáním , množiny zbytkových tříd , vektorové prostory se sčítáním, anebo nenulová reálna čísla spolu s operací násobení . Každá Abelova grupa se dá chápat jako modul nad okruhem celých čísel a naopak, modul nad okruhem celých čísel je Abelova grupa.
Konečné Abelovy grupy se dají jednoduše klasifikovat. Každá konečná Abelova grupa je izomorfní direktní sumě cyklických grup, jejichž řády jsou mocniny prvočísel. Speciální případ tohto tvrzení popisuje čínská věta o zbytcích, která byla částečně popsána už v knize Sun-c' suan-ťing čínského matematika Sun-c’ kolem mezi 3. a 5. stoletím. [28]
Obecněji, každá konečně generovaná Abelova grupa je součtem volných Abelových grup (izomorfních ) a cyklických grup řádů mocnin prvočísel.[29][30] Například racionální čísla spolu se sčítáním však nejsou konečně generovány. [31]
Dalším důležitým příkladem Abelových grup jsou Prüferovy grupy. Prüferova grupa je pro každé prvočíslo p spočetná Abelova grupa, v které má každý prvek p-tou odmocninu. Tyto grupy hrají důležitou roly v klasifikaci nekonečných Abelových grup.[32]
Podgrupa

Podgrupa grupy G je každá grupa, která je obsažena v grupě G. Formálněji Podgrupou grupy (G, •) se nazývá každá grupa (H, •), taková, že H ⊆ G. Ekvivalentně je podgrupa (G, •) každá množina H ⊆ G taková, že pro každé dva prvky h1, h2 ∈ H je i h1 • h2 ∈ H a také h1-1 ∈ H.
V příkladu Dehydrální grupy D4 popsaném výše, identita a rotace tvoří podgrupu zvýrazněnou v tabulce červenou barvou. Složení libovolných rotací je totiž opět rotace a inverze k rotaci je také rotace.
Samotná grupa G je vždy podgrupou G. Podobně jednoprvková grupa, která obsahuje jenom jednotkový prvek, je podgrupou G. Tyto podgrupy se nazývají triviální podgupry. Pokud K je podgrupa H a H je podgrupa G, je také K pogrupa G. Znalost struktury podgup dané grupy a důležitá pro prorozumění grupy jako celku, ačkoliv obecně grupa nemusí být jednoznačně určena strukturou svých vlastních podgrup.[33]
Pro libovolnou množinu S ⊆ G můžme definovat podgrupu generovanou S, která se skládá ze všech součinů prvků z S a jejich inverzí. Je to nejmenší podgrupa G obsahující množinu S.[34] Ve výše uvedeném příkladu podgrupa generována r2 a fv obsahuje kromě těchto dvou prvků také fv•r2=fh. Protože jak r2, tak fh, fv jsou samy k sobě inverzní a libovolný součin těchto prvků je opět prvkem množiny {id, r2, fv, fh}, jedná se o podgrupu. Tato podgrupa je komutativní.
Jednoduchá a polojednoduchá grupa
Pokud grupa neobsahuje žádné vlastní normální podgrupy, je označována jako jednoduchá grupa (někdy se též používá prostá grupa). Pokud grupa neobsahuje žádné vlastní normální Abelovy podgrupy, pak je označována jako polojednoduchá grupa (také poloprostá grupa).
U Lieových grup se definuje jednoduchá Lieova grupa jako taková, která neobsahuje žádné vlastní normální podgrupy kromě diskrétních.[35]
Homomorfizmus a izomorfizmus grup
Grupový homomorfizmus je zobrazení mezi grupami, které zachovává grupovou strukturu. Explicitně, a: G → H je homomorfizmus mezi (G,•) a (H,*), pokud pro libovolné 2 prvky g, k z G platí
- .
Z této definice se dá ukázat, že grupový homomorfizmus zobrazuje neutrální prvek eG v grupě G na neutrální prvek eH v grupě H a také inverzní prvek na inverzní:
Homomorfizmus tedy zachovává strukturu, která je určena grupovými axiomy.[36]
Dvě grupy G a H se nazývají izomorfní, pokud existují grupové homomorfizmy a: G→H a b: H→G takové, že složení a∘b=idH a b∘a=idH jsou identity. Zobrazení a se nazývá izomorfizmus grup.
Z abstraktního pohledu, izomorfní grupy jsou považovány za objekty reprezentující stejnou strukturu. Například vlastnost g•g=e v grupě G je ekvivalentní vlastnosti a(g)*a(g)=eH v grupě H.
Izomorfizmus G→G se nazývá automorfizmus. Každý prvek g∈G určuje vnitřní automorfizmus f(x)=g-1•x•g. Automorfizmus, který není vnitřní, se nazývá vnější.
Rozkladové třídy
V mnohých situacích je užitečné považovat dva prvky grupy za ekvivalentní, pokud se liší jenom o násobek nějaké dané podgrupy. Uvažujme například grupu D4 popsanou výše a její podgrupu R={id, r1, r2, r3}. Pokud uvažujeme nějaké překlopení čtverce (například fh), tak žádnou rotací už nemůžeme docílit zpátky konfiguraci id, r1, r2 nebo r3. Složení překlopení a rotace je vždy rotace. Rotace tedy nehraje roli, pokud si všímáme jenom, zda bylo nebo nebylo aplikováno nějaké překlopení.
Rozkladové třídy formalizují tuto ideu: podgrupa H grupy G definuje takzvané pravé a levé rozkladové třídy, definovány takto:[37]
Rozkladové třídy pro libovolnou podgrupu H tvoří rozklad G na disjunktní podmnožiny. Přesněji, sjednocení všech levých rozkladových tříd je celé G a libovolné dvě levé rozkladové třídy se buď rovnají, anebo jsou disjunktní.[38] První případ g1H = g2H nastává právě když g1-1•g2 ∈ H, t.j. když se příslušné prvky g1, g2 liší jenom o prvek z H. Analogická tvrzení platí pro pravé rozkladové třídy.
Pravé a levé rozkladové třídy se můžou, ale také nemusí rovnat. Pokud se rovnají, t.j. pokud pro všechna g v G platí gH = Hg, pak se podguupa H nazývá normální. Množina všech levých rozkladových tříd se značí G/H a množina všech pravých rozkladových tříd se značí H\G.
V případě grupy D4 z úvodu a její podgrupy rotací R, levé rozkladové třídy gR jsou buď množina R všech rotací (a identity) pokud g je prvkem R, anebo množina F={fh, fv, fd, fc} všech překlopení (zvýrazněna v tabulce zeleně) pokud g je nějaké překlopení. Levé rozkladové třídy jsou tedy D4/R={R, F}.
Normální podgrupa a faktorová grupa
- Hlavní článek: Faktorová grupa
Podgrupa N se nazývá normální podgrupou grupy G, pokud pro každé g∈G a n∈N existuje n'∈ N takové, že g•n=n'•g, t.j. levé a pravé rozkladové třídy se pro všechna g rovnají:
Ekvivalentně, H je jádro nějakého homomorfizmu grup G→K.[39] Každá podgrupa Abelovy grupy je normální.
Pokud N je normální podgupa G, je možné zavést na množině rozkladových tříd G/N={gN, g ∈ G} strukturu grupy.[40]. Grupová operace na množině G/N je definována vztahem (gN) • (hN) = (gh)N pro všechny g,h∈G. Tato grupa se nazývá faktorgrupa. Rozkladová třída e N=N je neutrální prvek této grupy a inverze k gN je třída (gN)−1 = (g−1)N. Z toho vidíme, že zobrazení G → G / N, které prvku g přiradí jeho rozkladovou třídu gN je homomorfizmus grup.[41]
| • | R | F |
|---|---|---|
| R | R | F |
| F | F | R |
| Tabulka násobení ve faktorové grupě D4 / R. | ||
V příkladu grupy D4 je její podgrupa R={id, r1, r2, r3} normální a rozkladové třídy jsou {R,F}, kde F je množina všech překlopení. Grupová operace na faktorové grupě je znázorněna tabulkou vpravo. Například F • F = fvR • fvR = (fv • fv)R = id R=R.
Podgrupa R je Abelova, a faktorová grupa D4/R je také Abelova, zatímco D4 není Abelova.
Generování a prezentace grupy
Faktorové grupy a podgrupy tvoří spolu způsob, kterým je možné každou grupu popsat její prezentací. Každou grupu je možné zadat jako faktor volné grupy nad nějakou generující množinou podle normální podgrupy generovanou relacemi.[42] Relace jsou výrazi, které se v grupě rovnají neutrálnímu prvku. Grupa zadána generátory a relacemi se zapisuje jako <Gen|Rel> kde Gen je množina generátorů a Rel množina relací.[43]
Dihedrální grupa D4 je generována například prvky r1 a fv, což znamená že každá symetrie čtverce se dá vyjádřit jako složení konečně mnoho týchto dvoch symetrií a jejich inverzí. Společně s relacema r14 = fv 2 = (r1 • fv)2 = 1,[44] je grupa úplně popsána. Tedy D4 = <r1, fv|r14, fv2, (r1•fv)2>.
Prezentace grupy se dá použít pro konstrukci Cayleyho grafu, který může graficky popsat diskrétní grupy.
Řešitelná grupa
Grupa G se nazývá řešitelná, pokud existuje posloupnost jejich podgrup
takových, že Gi+1 je normální podgrupa Gi a faktorová grupa Gi / Gi+1 je Abelova pro všechna i.[45]
Slovo řešitelná má historickou souvislost se zkoumáním existence řešení polynomiálních rovnic pomocí radikálů. Galois ukázal, že takové řešení existuje právě když grupa symetrií kořenů polynomu (tzv. Galoisova grupa) má výše uvedenou vlastnost.[46]
Příklady a aplikace
Čísla
Mnohé systémy čísel, například celá nebo racionální čísla mají přirozenou strukturu grupy. V některých případech jako například u racionálních čísel má jak sčítání tak i násobení grupovou strukturu. Takové číselné systémy se dají zobecnit na algebraické struktury jako jsou okruhy, tělesa, moduly, vektorové prostory a algebry.
Grupa celých čísel spolu se sčítáním byla popsána výše. Naproti tomu celá čísla s operací násobení () netvoří grupu. Asociativita je splněna, jednotkový prvek je číslo 1, ale k číslům obecně neexistují inverzní prvky (už pro celé číslo a = 2 rovnice ax=1 nemá řešení x v oboru celých čísel).
Pokud chceme, aby k nenulovým číslům existovaly inverzní prvky, musíme zavést zlomky a/b. Zlomky celých čísel se nazývají racionální čísla a množina racionálních čísel se značí . Množina nenulových racionálních čísel spolu s operací násobení je opět grupa. Součin dvou nenulových racionálních čísel je nenulové racionální číslo, neutrální prvek je 1 a inverzní prvek k nenulovému číslu a/b je nenulové číslo b/a. Racionální čísla (i s nulou) tvoří také grupu vzhledem ke sčítání.
Obecněji, množina všech prvků tělesa tvoří vždy grupu vzhledem ke sčítání a množina všech nenulových prvků tělesa tvoří grupu vhledem k násobení.
| • | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | 4 | 1 | 3 |
| 3 | 3 | 1 | 4 | 2 |
| 4 | 4 | 3 | 2 | 1 |
| Tabulka násobení v multiplikativní grupě . | ||||
Pro libovolné prvočíslo p, můžeme modulární aritmetikou zavést na množině zbytkových tříd násobení a je pak grupa.[47] Její prvky se dají reprezentovat jako třídy ekvivalence celých čísel s ekvivalencí n ~ m právě když p|m-n. Množina zbytkových tříd spolu se sčítáním a násobením je speciálním případem konečného tělesa.[48] Dá se ukázat, že každá multiplikativní grupa nenulových prvků konečného tělesa je cyklická.[49] Tyto grupy se používají v asymetrická kryptografii.
Tabulka vpravo znázorňuje multiplikativní grupu nenulových zbytkových tříd modulo 5. Rovnost 3•2=1 například znázorňuje fakt, že 3•2 mod 5=6 mod 5=1. Vidíme, že každý pravek má inverzní prvek (2-1=3, 4-1=4) a grupa je cyklická (například prvek 2 generuje celou grupu, neboť 21=2, 22=4, 23=3, 24=1.)
Další grupy, které pozůstávají z nějakých čísel, popisují následující příklady.
- Množina Gaussových čísel , zobecňuje celá čísla do komplexní roviny.
- Množina invertibilních prvků v obecné množině zbytkových tříd tvoří vzhledem k násobení grupu.
- Množina komplexních čísel absolutní hodnoty 1 spolu s násobením tvoří grupu (značí se S1).
- Množina kvaternionů normy 1 spolu s násobením tvoří grupu (značí se S3).
- Kvaternionová grupa je grupa o osmi prvcích, generována prvky {1,i,j,k} v grupě nenulových kvaternionů.
Grupy symetrií

Grupa symetrií je grupa, jejíž prvky jsou symetrie daného matematického objektu, ať už geometrického (jako grupa symetrií čtverce v úvodu) anebo algebraického, například kořeny polynomu.[50] Teorie grup může být chápana jako studium symetrií. Dá se například dokázat, že každá grupa je grupou symetrie nějakého grafu.[51] Symetrie v matematice často zjednodušuje studium geometrických, analytických anebo fyzikálních objektů. O grupě se říká, že má akci na objektu X pokud každý prvek grupy provede s objektem operaci kompatibilní s grupovou struturou. Symetrie objektu je pak podgrupa všech takových prvků, které nechávají X nezměněn.
Symetrie dláždění roviny
Rovinné krystalografické grupy (anglicky Wallpaper groups) popisují symetrie periodických dláždění roviny. V příkladu na obrázku vpravo je vzorek tvořen kytkou, která se periodicky opakuje. Grupa symetrií tohto vzoru obsahuje všechny takové transformace roviny, které převádí vzor sám na sebe. Tato grupa se skládá jenom s translací a neobsahuje žádné rotace ani zrcadlení. Jiná periodická dláždění (například nekonečný čtverečkový papír) mají grupu symetrií, která obsahuje kromě translací roviny i různé rotace, zrcadlení a jejich složení. Různých neizomorfních rovinných krystalografických grup existuje celkem 17. Tyto vzory můžme najít často v islámské architektuře, většina z nich se vyskytuje například v paláci Alhambra.[52] Důkaz, že rovinných krystalografických grup je právě 17, publikoval poprvé E.Fedorov v roce 1891.[53] Kromě těchto dláždění roviny existují i neperiodická dláždění, jejichž grupa symetrií neobsahuje žádnou translaci. Příkladem je slavné Penroseho pokrytí, což je neperiodické dláždění roviny pomocí konečného počtu typů dlaždiček. Jeho grupa symetrie obsahuje například otočení o pětinu kruhu kolem nějakého bodu.[54]

Podobná periodická dláždění a jejich grupy symetrií můžeme studovat i v neeukleidovských geometriích. Příklad na obrázku vpravo zobrazuje pokrytí hyperbolické roviny trojúhelníky. Příslušná grupa symetrie se nazývá trojúhelníková grupa (v tomto případě (2,3,7)). Prvek řádu 7 trojúhelníkové grupy (2,3,7) (anglicky (2,3,7) triangle group) má akci na hyperbolické rovině, která "otočí" rovinu kolem bodu o 1/7 kruhu takovým způsobem, že převede dláždění samo na sebe.
Symetrie v krystalografii
V chemických oborech jako krystalografie popisují prostorová grupa a bodová grupa molekulární symetrie a symetrie krystalů. Tyto symetrie určují chemické a fyzikální vlastnosti těchto systémů a teorie grup v mnohých případech usnadňuje kvantově mechanickou analýzu těchto vlastností.[55][56] Například teorie grup ukazuje že některé přechody mezi kvantovými stavy nemůžou nastat jenom z důvodu symetrií daných stavů.
Nejenom že jsou grupy užitečné na popis symetrií molekul, ale překvapivě dokážou i predikovat, jak molekuly můžou svoji symetrii změnit. Jahn-Tellerův jev je deformace molekuly s vysokou mírou symetrie, která nabude určitý stav, jehož symetrie je z množiny nižších symetrií, které jsou ale vzájemně příbuzné a souvisejí se symetrií původní.[57][58] Podobně, teorie grupa může být použita pro popis změn fyzikálních vlastností, které se dějou u fázového přechodu, například při změně typu mřížky.[2]

|

|

|

|
| Molekula Buckminsterfullerenu C60 má icosahedrální symmetrii. |
Amoniak NH3. Jeho grupa symetrie má řád 6 a je generována rotací o 120° a zrcadlením. | Molekula kubanu C8H8 vykazuje oktahedrální symmetrii. |
Komplexní sloučenina Hexaaquacopper(II), Cu[(OH2)6]2+.
Ve srovnání s úplně symetrickým tvarem, molekula je vertikálně odkloněna o asi 22% (Jahn-Tellerův jev). |
Transformační grupy v geometrii
Geometrické vlastnosti, které akce grupy nemění, studuje geometrická teorie invariantů.[59] Felix Klein ve slavné přednášce v Erlangen v roce [1872] definoval geometrii takto:[60]
Geometrie je studium invariantů vůči grupě transformací.
Grupa symetrie nějaké geometrie je množina všech transformací, které zachovávájí příslušnou geometrickou strukturu. Například pro Eukleidovu geometrii je to takzvaná Eukleidova grupa Euc(n), která se skládá se všech translací, rotací a zrcadlení n-rozměrného Eukleidova prostoru. Akce této grupy zachovává vzdálenosti bodů, a velikosti a úhly vektorů. Podobně pro projektivní geometrii pozůstává příslušná grupa symetrie ze všech kolineací, které zachovávají projektivní invarianty (převádí projektivní přímky na projektivní přímky a zachovávají dvoupoměr).
Tyto grupy symetrií nějaké geometrie se nazývají transformační grupy a pro běžné geometrie jsou to tzv. Lieovy grupy. Pokud je Liova grupa G transformační grupa nějakého geometrického prostoru X a G má na X tranzitivní akci, můžme definovat podgrupu H ⊆ G všech transformací, které zachovávají jistý bod x ∈ X. Prostor X pak můžme ztotožnit s prostorem rozkladových tříd
Tento popis geometrie se nazývá Kleinova geometrie.[61] Speciální volba grup G,H vede na Eukleidovskou, afinní a projektivní geometrii. Následuje tabulka, která popisuje některé geometrické struktury a jejich příslušnou transformační grupu G.
| Podkladový prostor | Transformační grupa G | Invarianty | |
| Eukleidova geometrie | Eukleidův prostor | Eukleidova grupa Euc(n) | Vzdálensti bodů, úhly vektorů |
|---|---|---|---|
| Sférická geometrie | Sféra Sn | ortogonální grupa O(n+1) | Vzdálensti bodů, úhly vektorů |
| Konformní geometrie na sféře | Sféra Sn | Lorentzova grupa n+2 dimenzionálního prostoru O(n+1,1) | Úhly vektorů |
| Projektivní geometrie | Projektivní prostor | projektivní grupa PSL(n+1) | Projektivní přímky, dvoupoměr |
| Afinní geometrie | Afinní prostor | afinní grupa Aff(n) | Přímky, poměry obsahů geometrických útvarů, těžiště trojúhelníků. |
| Popis něterých geometrií pomocí jejich transformačních grup. | |||
Zobecnění těchto idejí na širší třídu geometrií zahrnujících zakřivené prostory v Riemannově geometrii rozpracoval Élie Cartan.
Obecná linární grupa a teorie reprezentací

Maticové grupy jsou grupy, které se skládají z matic a grupová operace je maticové násobení. Obecná lineární grupa GL(n, R) se skládá ze všech regulárních reálnych čtvercových matic dimenze n.[62] Její podgrupy se nazývají maticové grupy anebo lineární grupy. Dihedrální grupa v úvodu se dá reprezentovat jako maticová grupa (symetrie čtverce jako otočení nebo překlopení můžme reprezentovat maticí). Jiná důležitá maticová grupa je speciální ortogonální grupa SO(n). Popisuje všechny možné rotace v n rozměrném Eukleidově prostoru.
Teorie reprezentací je jak aplikace grupových konceptů, tak i důležitý nástroj pro hlubší porozumění grup.[63] [64] Tato teorie studuje grupy pomocí jejich akcí na vektorových prostorech. Reprezentace grupy G na vektorovém prostoru V je grupový homomorfizmus
- ρ: G → GL(V)
grupy G a obecné lineární grupy GL(V). Tímto způsobem se grupová operace na G, která mohla být zadána abstraktním způsobem, převede na skládání lineárních zobrazení, resp. násobení matic, což umožňuje explicitní počty.[pozn 1] Grupová akce na nějakém prostoru je tedy prostředkem jak ke zkoumání daného prostoru, tak i ke zkoumání grupy samotné. Teorie reprezentací dává do souvislosti teorii konečných grup, Lieových grup, algebraických grup a topologických grup, hlavně (lokálně) kompaktních grup.[65][66]
Reprezentace Lieových grup mají aplikace v geometrii a studium reprezentací grup v prostorech nenulové charakteristiky má aplikace v teorii čísel.[67] Některé partie teorie reprezentací jsou zobecněním klasické harmonické analýzy studující funkce prostřednictvím Fourierovy transformace.[68][69][70]
Galoisova grupa
Galoisova grupa byla vynalezena pro popis řešení polynomických rovnic. Například řešení kvadratické rovnice x2 + px + q = 0 jsou dány
Podobné vzorce jsou známe pro kubické a kvartické rovnice, ale neexistují pro rovnice pátého stupně a vyšší.[71]
Výměna "+" a "−" v tomto výrazu, tj. permutace obou kořenů rovnice se dá chápat jako velmi jednoduchá grupová operace. Kořeny původní rovnice splňují x1x2=q, x1+x2=-p. Zároveň výměna kořenů x1 a x2 nemění jejich součet a součin. Pro obecný polynom se dá definovat Galoisova grupa jako množina všech takových permutací kořenů, že racionální výrazy kořenů (například x1+x2 nebo x1x2), které popisují nějaký racionální výraz koeficientů (například -p nebo q), se nemění (x1+x2=x2+x1 a pod).
Abstraktní vlastnosti Galoisovy grupy asociované s polynomem dávají kritérium, zda má polynom všechny své kořeny vyjádřitelné z koeficientů pomocí radikálů, t.j. pomocí sčítání, násobení a n-tých odmocnin. Je to právě když příslušná Galoisova grupa je řešitelná.[72] Pro některé polynomy stupně 5 však Galoisova grupa pozůstává se všech permutací pěti kořenů.[73] Permutační grupa S5 však není řešitelná[74] a proto obecný vzorec pro rovnice pátého stupně, který by obsahoval pouze sčítání, násobení, dělení a odmocňování, nemůže existovat.
V moderní algebře se Galoisova grupa definuje obecněji pro tělesa jejich rozšíření. Pokud je E nadtěleso tělesa F, je příslušná Galoisova grupa Gal(E/F) definována jako množina všech automorfizmů tělesa E, které nemění prvky tělesa F. Základní věta Galoisovy teorie tvrdí, že podgupy Galoisovy grupy odpovídají mezitělesům F ⊆ K ⊆ E.[75]
Grupy v algebraické topologii

V algebraické topologii se topologickým prostorům přirazují různé grupy, které reflektují jejich vlastnosti. Nejjednodušší je tzv. fundamentální grupa, kterou jako první uvažoval Camille Jordan[76] a formálně definoval Henri Poincaré.[77]
Prvky fundamentální grupy se dají reprezenrovat jako smyčky (uzavřené křivky) v daném prostoru. Dvě smyčky reprezentují stejný prvek fundamentální grupy, pokud se dají jedna na druhou převést spojitou deformací. Obrázek vpravo uazuje křivku v rovině bez bodu. Modrá křivka se považuje za triviální a reprezentuje neutrální prvek fundamentální grupy, neboť se dá spojitě stahnout do jednoho bodu. Naopak oranžová křivka se stahnout nedá, protože uvnitř ní je díra (chybějící bod). Fundamentální grupa roviny, z které odstraníme jeden bod, je nekonečná cyklická grupa generována oranžovou křivkou.
Podobně se definují vyšší homotopické grupy, které mohou odhalit díry různých dimenzí.[78] Homotopické grupy jsou topologické a dokonce i homotopické invarianty, to znamená, že prostory, které jsou topologicky evivalentní (homeomorfní) a dokonce i prostory, které jsou homotopické resp. homotopicky ekvivalentní, mají izomorfní homotopické grupy. Spojitá zobrazení topologických prostorů indukují přirozeným způsobem homomorfizmy jejich homotopických grup. Homotopické grupy jsou tedy speciálním případem kovariantního funktora.[79]
Výpočet vyšších homotopických grup je však často velmi složitý. Dodnes nejsou obecně známy ani homotopické grupy sfér, ačkoliv je známo, že jejich výpočet je algoritmicky možný.[80] Proto se často používají jednodušší homologické a kohomologické grupy.[81] Tyto grupy jsou taktéž homotopické invarianty. Homologie n té dimenze Hn je kovariantní funktor z kategorie topologických prostorů do kategorie grup. Podobně Hn je kontravariantní funktor.
Využitím homotopických a homologických grup je možné řešit širokou třídu topologických problému: například dokázat neexistence rozšiření spojitého zobrazení s podprostoru na celý prostor (například identita na sféře se nedá rozšířit na zobrazení celé koule na sféru),[82], dokazovat různé věty o pevných bodech (například Browerova věta o pevném bodu)[83], dokázat základní větu algebry,[84] anebo ukázat, že otevřené množiny v Eukleidovských prostorech jsou homeomorfní pouze pokud mají stejnou dimenzi (a tedy dimenze prostoru je topologický invariant).[85]
Další využití
Existuje rada dalších teoretických i praktických aplikací teorie grup. Konečné grupy symetrií, jako například Mathiovy grupy se využívají v kódování a v korekci chyb přenášených dat (forward error correction, FEC), a také v CD přehrávačech.[86] Diferenciální Galoisova teorie, charakterizuje funkce s danou antiderivací, která dává gruppově teoreticá kritéria pro vlastnosti řešení jistých diferenciálních rovnic.[87] Grupy se podstatným způsobem využívají v algebraické geometrii a teorii čísel.[88] Kryptografie kombinuje přístup abstraktní teorie grup s výpočetní teorií grup implementovanou pro konečné grupy.[89]
Aplikace teorie grup nejsou omezeny na matematiku a z jejích konceptů také čerpají vědy jako chemie, fyzika a informatika.
Konečné grupy
Grupa se nazývá konečná, pokud má konečně mnoho prvků. Počet jejich prvků se nazývá řád grupy.[90] Důležitý příklad je grupa permutací n-prvkové množiny Sn, která se také nazývá symetrická grupa.[91] Například symetrickou grupu S3 můžme reprezentovat jako množinu permutací tří písmen ABC. Grupa pozůstává z prvků ABC, ACB, ..., až po CBA, celkem 6 prvků. Symetrické grupy jsou základním příkladem konečných grupy, neboť každá konečná grupa se dá vyjádřit jako podgrupa symetrické grupy Sn pro vhodné přirozené číslo n (Cayleyho věta). [92] Grupa S3 se dá interpretovat jako množina symetrií rovnostranného trojúhelníka, podobně jako dihedrální grupa D4 v úvodu je grupou symetrií čtverce.
Řád prvku a grupy G je nejmenší přirozené číslo n takové, že an (součin n kopií a) je rovno neutrálnímu prvku e. Řád každého prvku konečné grupy je konečný. Grupa je do jisté míry určena svým řádem a strukturou svých podgrup. Lagrangeova věta tvrdí, že pro konečnou grupu G počet prvků její libovolné podgrupy H dělí počet prvků grupy G.[93] Sylowovy věty dávají část obráceného tvrzení.[94]

Dihedrální grupa (uvedena výše) je příkladem konečné grupy řádu 8. Řád prvku r1 je 4, stejně jako řád podgrupy R kterou generuje. Řád libovolné reflexe je 2. Oba řády dělí číslo 8, jak tvrdí Lagrangeova věta. Malé grupy se dají částečně popsat grafem cyklů, v kterém vrcholy grafu odpovídají prvkům grupy a cyklickým podgrupám {a,a2,...,an=e} odpovídají hrany od a k a2, od a2 k a3 a tak dál. Obrázek vpravo znázorňuje graf cyklů Dihedrální grupy D4. Pro grupy řádu menšího než 16 určuje graf cyklů grupu jednoznačně.
Další důležité příklady konečných grup jsou multiplikativní grupy konečných těles a grupy regulárních, ortogonálních respektive symplektických matic nad konečnými tělesy.
Klasifikace jednoduchých konečných grup
Zatím co klasifikace konečných Abelových grup je jednoduchá, snaha o klasifikaci všech konečných grup vede na hluboké a složité matematické problémy. Podle Lagrangeovy věty, konečné grupy prvočíselného řádu p jsou nutně cyklické a tedy izomorfní grupě . O grupách řádu p2 víme že jsou Abelovy, toto tvrzení už ale neplatí pro grupy řádu p3, jak ukazuje příklad dihedrální grupy D4 řádu 8 = 23.[95] Grupy nízkých řádů se dají popsat i pomocí počítačových programů (např. computer algebra system). Malé grupy jsou známe až do řádu 2000 a až na izomorfizmus jich je kolem 50 miliard. [96][pozn 2] Klasifikace všech jednoduchých grup však zatím není známa.
Mezistupeň v porozumění konečných grup představuje klasifikace konečných jednoduchých grup.[pozn 3] Netriviální grupa se jmenuje jednoduchá, pokud jediné její normální podgrupy jsou grupa triviální (jednoprvková) a celá grupa. Jordan–Hölderova věta popisuje jednoduché grupy jako základní prvky pro konstrukci obecných konečných grup. [97]
Dokončení seznamu všech konečných jednoduchých grup byl velký úspěch současné teorie grup. Věta o klasifikaci jednoduchých konečných grup říká, že každá konečná jednoduchá grupa spadá buďto do jedné z 18 nekonečných skupin grup nebo je jednou z 26 takzvaných sporadických grup.[98][pozn 4] Tato věta plně charakterizuje všechny konečné jednoduché grupy. Kvůli ohromné náročnosti jejího důkazu bývá v angličtině také nazývána „Enormous theorem“.
Důkaz této věty nebyl nikdy uveřejněn v celku. Sestává z více než 500 článků od přibližně 100 autorů uveřejněných v nejrůznějších matematických časopisech převážně mezi lety 1955 a 1983. Odhaduje se, že celková délka důkazu je 10 000–15 000 stran tištěného textu.[99] Taková rozsáhlost může vyvolat (podobně jako u věty o čtyřech barvách) pochybnosti o správnosti důkazu. Žádný matematik totiž pravděpodobně nepřečetl tento důkaz celý, a tedy nikdo na světě nemůže sám o sobě tvrdit, že v něm není chyba. Každá jednotlivá část důkazu publikovaná v průběhu téměř třiceti let však byla mnoha matematiky přečtena a uznána za správnou. Proto je tento důkaz všeobecně považován za správný.
Nositel Fieldsovy medaile Richard Borcherds dokázal tzv. monstrous moonshine hypotézy, překvapivě hlubokou souvislost největší jednoduché sporadické grupy, tzv. monstergrupy, s jistými modulárními formamy, které patří do hraničné vědy mezi komplexní analýzou a teorií strun.[100]
Grupy s dodatečnou strukturou
Mnoho grup jsou současně příklady jiných matematických struktur. V jazyku teorie kategorií jsou to grupové objekty nějaké kategorie, tedy objekty a morfizmy, které jsou kompatibilní s grupovou strukturou.
Topologické grupy

Některé topologické prostory můžou být vybaveny grupovým násobením. Abychom takovou grupu nazvali topologickou grupu, musí být obě operace vzájemně kompatibilní, což znamená že grupové násobení g • h závisí spojitě na g a h a také inverze g-1 je spojitou funkcí g.[101]
Nejzákladnějším příkladem jsou reálna čísla spolu se sčítáním , nenulová reálna čísla s násobením a podobně libovolné topologické těleso, jako například komplexní čísla anebo p-adická čísla. Všechny tyto grupy jsou lokálně kompaktní, je na nich tedy možné definovat invariantní Haarovu míru.[102] Díky ní je možné na grupě integrovat a studovat vlastnosti grupy pomocí harmonické analýzy. Invariance v tomto případě znamená, že
pro libovolný prvek grupy c.
Maticové grupy nad těmito tělesy jsou také lokálně kompaktní topologické grupy a taktéž adély a adelické algebraické grupy, které jsou důležité v teorii čísel.[103]
Galoisovy grupy rozšíření těles nekonečného stupně jako například absolutní Galoisova grupa, se dají přirozeně vybavit tzv. Krullovou topologií.[104] Zobecněním těchto idejí adaptovaným na potřeby algebraické geometrie, je etální fundamentální grupa.[105]
Lieovy grupy
- Hlavní článek: Lieova grupa
Lieovy grupy (pojmenovány po Sophusi Lieovi) jsou grupy, které mají současně strukturu hladké variety, t.j. jsou lokálně difeomorfní Eukleidovskému prostoru dané dimenze.[106] Struktura variety musí být opět kompatibilní se strukturou grupy, t.j. v tomto případě násobení a inverze musí být hladká (t.j. diferencovatelné) zobrazení.
Příkladem Lieovy grupy je obecná lineární grupa, která se skláda ze všech regulárních reálnych nebo komplexních matic dimenze n×n. Je to otevřená množina v prostoru všech matic n×n, neboť je určena nerovností
- det (A) ≠ 0,
kde A je matice.[107] Kromě obecné lineární grupy existují další série Lieových grup, které se nazývají klasické grupy. Jsou to Speciální lineární grupa, která pozůstává pouze s matic s determinantem rovným jedné, ortogonální lineární grupy, unitární grupy a symplektické grupy.
Lieovy grupy mají úzkou souvislost s Lieovýma algebrama. Lieova algebra Lieovy grupy popisuje lokální vlastnosti grupy.[108][109] Wilhelm Killing a Élie Cartan popsali klasifikaci jednoduchých Lieových algeber nad komplexními čísly a reálnými čísly. Každá komplexní jednoduchá Lieova algebra patří do 4 nekonečných sérií anebo je jednou z pěti výjimečných Lieových algeber.[110] Grupy, které k těmto algebrám náleží, jsou (až na nakrytí) speciální lineární grupy, ortogonální lineární grupy liché a sudé dimenze, symplektické grupy a výjimečné Lieovy grupy (vše nad komplexními čísly). K těmto komplexním grupám existuje vícero reálnych forem (ke každé existuje právě jedna kompaktní).[111]
Lieovy grupy mají zásadní důležitost ve fyzice: Noetherové věta dává do souvislosti symetrie a kvantity, které se zachovávají.[112] Rotace, podobně jako translace v prostoru a času jsou základní symetrie zákonů klasické mechaniky. Jiný jednoduchý příklad tvoří Lorentzovy transformace, které dávají do souvislosti měření polohy a času ve speciální teorii relativity.[113] Množina všech takových transformací se nazývá Lorentzova grupa a tvoří rotační symetrie Minkowského prostoru, který je model časoprostoru v teorii relativity při absenci hmoty. Grupa všech symetrií Minkowského prostoru, která zahrnuje i translace, se nazývá Poincarého grupa. Tato Lieova grupa hraje hlavní roli v speciální teorii relativity a také v kvantové teorii pole. Unitární grupy SU(2) a SU(3) vystupují jako grupy symetrií některých částicových teorií a výjimečné Lieovy grupy E8 se vyskytují často v teorii strun a kvantové gravitaci.[114].
Důležitou součástí studia Lieových grup je studium jejich reprezentací. Tyto reprezentace mají aplikace v geometrii a díky nim je možné také zobecnit klasickou harmonickou analýzu, která studuje funkce prostřednictvím jejich Fourierovy transformace, na funkce definované na Lieových grupách.[70]
Zobecnění
| Asociativita | Neutrální prvek | Inverzní prvek | Komutativita | |
|---|---|---|---|---|
| Abelova grupa | ||||
| Grupa | ||||
| Monoid | ||||
| Pologrupa | ||||
| Lupa | ||||
| Kvazigrupa | ||||
| Grupoid |
V abstraktní algebře je možné definovat obecnější struktury vynecháním některých axiomů grupy.[115][116] Pokud například vynecháme v definici grupy požadavek, aby ke každému prvku existoval inverzní prvek, výsledná algebraická struktura se nazývá monoid. Množina přirozených čísel (včetně nuly) spolu se sčítáním tvoří monoid, podobně množina všech celých čísel spolu s operací násobení. Existuje obecná metoda jak formálně přidat inverzní prvky k libovolnému Abelovému monoidu podobným způsobem jako jsou odvozena racionální čísla od a takto vzniklá grupa se nazývá Grothendieckova grupa. Dalším příkladem algebraické struktury je kvazigrupa, v které sice neexistuje neutrální prvek, přesto je ale možné dělit, t.j. rovnice a•x=b a x•a=b mají řešení pro každé a a b. Struktura, v které je dána pouze binární operace bez žádných dalších předpokladů o ní, se nazývá grupoid.
Další matematické pojmy zobecňující grupu jsou morfizmy nějaké kategorie. Morfizmy se dají skládat, a jejich složení splňuje asociativní zákon, ovšem obecně nemusí existovat inverzní morfizmy a také není možné složit libovolné morfizmy (jenom prvky Mor(A,B) a Mor(B,C)). Kategorie, v které je každý morfizmus izomorfizmem, se nazývá grupoid v teorii kategorií. Morfizmy tohto objektu splňujou asociativitu, existenci neutrálního i inverzního prvku, ovšem opět je možné skládat jenom takové morfizmy, že složení má smysl.
Libovolný z těchto konceptů se dá dále zobecňovat na obecnou n-ární operaci (t.j. operace, která má jako vstup n argumentů). Vhodným zobecněním axiomů grupy dostáváme tzv. n-ární grupu.[117]
Odkazy
Poznámky
- V tomto článku byl použit překlad textu z článku Group (mathematics) na anglické Wikipedii.
- ↑ Tato věc se byla klíčová pro klasifikaci jednoduchých konečných grup, viz např. Aschbacher, Michael (2004), The Status of the Classification of the Finite Simple Groups (PDF), Notices of the American Mathematical Society 51 (7): 736–740.
- ↑ Naprostá většina z nich je řádu 1024.
- ↑ Mezera mezi klasifikací jednoduchý group a všech grup spočívá v problému extenze, který je příliš obtížný na obecné řešení. Viz např. Aschbacher (2004), The Status of the Classification of the Finite Simple Groups, str. 737.
- ↑ Největší z nich, tzv. monstergrupa, obsahuje asi prvků.
Související články
- Algebraická struktura
- Akce grupy na množině
- Fundamentální grupa
- Grupoid
- Generování grupy
- Invariant
- Monoid
- Okruh (algebra)
- Pologrupa
- Symetrie
- Reprezentace grupy
Reference
- ↑ RAMOND, Pierre. Group Theory: A Physicist's Survey. [s.l.]: Cambridge University Press, 2010. 310 s. ISBN 9780521896030. S. 5. (anglicky)
- ↑ a b c Tento axiom je implicitně obsažen v tom, že je binární operace na a někdy se proto vynechává. Chybná citace: Neplatná značka
<ref>; název „pozn“ použit vícekrát s různým obsahem - ↑ PLOTKIN, Boris Isaakovich. Universal algebra, algebraic logic, and databases. [s.l.]: Springer, 1994. 438 s. ISBN 9780792326656. S. 48. (anglicky)
- ↑ ROSICKÝ, Jiří. Algebra. 4 (1.dotisk). vyd. Brno: Masarykova univerzita, 2005. 133 s. ISBN 80-210-2964-1. Kapitola 1, s. 9.
- ↑ a b PROCHÁZKA, Ladislav, a kol. Algebra. Praha: Academia, 1990. 560 s. ISBN 80-200-0301-0. Kapitola III., s. 100.
- ↑ VALVODA, Václav; POLCAROVÁ, Milena; LUKÁČ, Pavel. Základy strukturní analýzy. 1.. vyd. Praha: Karolinum, 1992. 489 s. ISBN 80-7066-648-X.
- ↑ WUSSING, Hans. The Genesis of the Abstract Group Concept: A Contribution to the History of the Origin of Abstract Group Theory. New York: Dover Publications, 2007. ISBN 978-0-486-45868-7. (anglicky)
- ↑ KLEINER, Israel. The evolution of group theory: a brief survey. Mathematics Magazine. 1986, s. 195–215. DOI 10.2307/2690312.
- ↑ SMITH, David Eugene. History of Modern Mathematics. [s.l.]: [s.n.], 1906. Dostupné online. (anglicky)
- ↑ The History Behind The Quadratic Formula
- ↑ O'Connor, John J.; Robertson, Edmund F., Lodovico Ferrari, MacTutor History of Mathematics archive, University of St Andrews.
- ↑ GALOIS, Évariste. Manuscrits de Évariste Galois. Paris: Gauthier-Villars, 1908. Dostupné online. (francouzsky) (Galoisovo dílo bylo prvně publikováno Josephem Liouvillem v roce 1843)
- ↑ Kleiner, str. 202
- ↑ Wussig, §III.2
- ↑ LIE, Sophus. Gesammelte Abhandlungen, Band 1. New York: Johnson Reprint Corp., 1973. (německy).
- ↑ Kleiner, str. 204
- ↑ Wussig, §I.3.4
- ↑ JORDAN, Camille. Traité des substitutions et des équations algébriques. Paris: Gauthier-Villars, 1870. (francouzsky)
- ↑ VON DYCK, Walther. Gruppentheoretische Studien. Mathematische Annalen. 1882, s. 1–44. DOI 10.1007/BF01443322.
- ↑ CURTIS, Charles W. Pioneers of Representation Theory: Frobenius, Burnside, Schur, and Brauer. Providence, R.I.: American Mathematical Society, 2003. ISBN 978-0-8218-2677-5. (anglicky).
- ↑ MACKEY, George Whitelaw. The theory of unitary group representations. [s.l.]: University of Chicago Press, 1976. (anglicky)
- ↑ BOREL, Armand. Essays in the History of Lie Groups and Algebraic Groups. Providence, R.I.: American Mathematical Society, 2001. ISBN 978-0-8218-0288-5. (anglicky)
- ↑ ASCHBACHER, Michael. The Status of the Classification of the Finite Simple Groups. Notices of the American Mathematical Society. 2004, s. 736–740. Dostupné online.
- ↑ LANDIN, Joseph. An introduction to algebraic structures. [s.l.]: Courier Dover Publications, 1989. 247 s. ISBN 9780486659404. S. 68, definice 8. (anglicky)
- ↑ LANG, Serge. Undergraduate Algebra. Berlin, New York: Springer, 2005. ISBN 978-0-387-22025-3. Kapitola §II.1, s. 22. (anglicky)
- ↑ MAC LANE, S.; BIRKHOFF, G. Algebra. Bratislava: Vydavateľstvo technickej a ekonomickej literatúry, 1974. Kapitola III (grupy), s. 106, Veta 4,5. (slovensky)
- ↑ JACOBSON, Nathan. Basic algebra. [s.l.]: American Mathematical Society, 2009. ISBN 978-0-486-47189-1. S. 41. (anglicky)
- ↑ The MacTutor History of Mathematics archive, Sun Zi
- ↑ HUNGERFORD, Thomas W. Algebra. [s.l.]: Springer, 1996. 502 s. ISBN 9780387905181. Kapitola 2, věta 2.2, s. 76. (anglicky)
- ↑ Wolf Holzmann, Classification of Finitely Generated Abelian Groups (online)
- ↑ LA HARPE, Pierre. Topics in geometric group theory. [s.l.]: AMS, 2000. ISBN 9780226317212. S. 46. (anglicky)
- ↑ HAZEWINKEL, Michiel. Encyclopaedia of mathematics. [s.l.]: Springer, 1995. 3748 s. ISBN 9781556080104. S. 13-14. (anglicky)
- ↑ SUZUKI, Michio. On the lattice of subgroups of finite groups. Transactions of the American Mathematical Society. 1951, s. 345–371. DOI 10.2307/1990375. JSTOR 1990375.
- ↑ LEDERMANN, Walter. Introduction to group theory. New York: Barnes and Noble, 1973. Kapitola II.12, s. 39. (anglicky)
- ↑ MOTL, Luboš; ZAHRADNÍK, Miloš. Pěstujeme lineární algebru. Praha: Karolinum, 1997. Dostupné online. ISBN 9788071841869. Kapitola Grupa. (anglicky)
- ↑ Lang 2005, kap. §II.3, s. 34
- ↑ Lang 2005, II.4, s. 41
- ↑ LANG, Serge. Algebra. New York: Springer, 2002. ISBN 978-0-387-95385-4. Kapitola §I.2, s. 12. (anglicky)
- ↑ Lang 2005, §II.4, s. 45
- ↑ Lang 2005, §II.4, p. 45
- ↑ Lang 2005, §II.4, s. 46. Cor. 4.6.
- ↑ BOGOPOLʹSKIJ, Oleg Vladimirovič. Introduction to group theory. [s.l.]: European Mathematical Society, 2008. 177 s. ISBN 9783037190418. Kapitola 5, s. 58. (anglicky)
- ↑ Bogopolʹskij, s. 59
- ↑ Lang, 2002, §I.2, p. 9
- ↑ Lang 2005, §II.4, s. 49
- ↑ EDWARDS, Harold M. Galois theory. [s.l.]: Springer, 1984. 152 s. ISBN 9780387909806. S. 89, (Theorem). (anglicky)
- ↑ Lang 2005, Kap. VII
- ↑ WAN, Zhe-Xian. Lectures on finite fields and galois rings. [s.l.]: World Scientific, 2003. 342 s. ISBN 9789812385703. S. 103. (anglicky)
- ↑ Wan, str. 115, Theorem 6.3
- ↑ WEYL, Hermann. Symmetry. [s.l.]: Princeton University Press, 1983. 342 s. ISBN 978-0-691-02374-8. S. 103. (anglicky)
- ↑ FRUCHT, R. Herstellung von Graphen mit vorgegebener abstrakter Gruppe [Construction of Graphs with Prescribed Group]. Compositio Mathematica. 1939, s. 239–50. Dostupné online..
- ↑ Branko Grünbaum, What Symmetry Groups Are Present in the Alhambra?, notices of AMS, vol. 53, n. 6
- ↑ E. Fedorov (1891) "Simmetrija na ploskosti" [Symmetry in the plane], Zapiski Imperatorskogo Sant-Petersburgskogo Mineralogicheskogo Obshchestva [Proceedings of the Imperial St. Petersburg Mineralogical Society], series 2, vol. 28.
- ↑ David Austin, Penrose Tiles Talk Across Miles, Math Samplings (AMS)
- ↑ CONWAY, John Horton; DELGADO FRIEDRICHS, Olaf; HUSON, Daniel H.; THURSTON, William P. On three-dimensional space groups. Beiträge zur Algebra und Geometrie. 2001, s. 475–507. arXiv math.MG/9911185.
- ↑ BISHOP, avid H. L. Group theory and chemistry. New York: Dover Publications, 1993. ISBN 978-0-486-67355-4. (anglicky)
- ↑ BERSUKER, Isaac. The Jahn-Teller Effect. [s.l.]: Cambridge University Press, 2006. ISBN 0-521-82212-2. S. 2. (anglicky)
- ↑ JAHN, H.; TELLER, E. Stability of Polyatomic Molecules in Degenerate Electronic States. I. Orbital Degeneracy. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences (1934–1990). 1937, s. 220–235. DOI 10.1098/rspa.1937.0142.
- ↑ MUMFORD, David; FOGARTY, J.; KIRWAN, F. Geometric invariant theory. Berlin, New York: Springer-Verlag, 1994. (3). ISBN 978-3-540-56963-3. (anglicky)
- ↑ GALARZA, A.I.R.; SEADE, J. Introduction to Classical Geometries. [s.l.]: Birkhäuser Basel, 2007. ISBN 978-3764375171. S. 16. (anglicky), dostupné online
- ↑ SHARPE, R.W. Differential Geometry: Cartan's Generalization of Klein's Erlangen Program. [s.l.]: Springer, 1997. ISBN 978-0387947327. (anglicky) Transformace známých geometrií jsou popisovány pomocí Lieových grup a naopak, studium Lieových grup vedlo k popisu nových geometrických struktur.
- ↑ REES, Elmer G. Notes on geometry. [s.l.]: Springer, 1988. ISBN 9783540120537. S. 3. (anglicky)
- ↑ FULTON, William.; HARRIS, Joe. Representation theory. A first course. New York: Springer, 1991. ISBN 978-0-387-97495-8. (anglicky)
- ↑ SERRE, Jean-Pierre. Linear representations of finite groups. New York: Springer, 1977. ISBN 978-0-387-90190-9. (anglicky)
- ↑ Fulton-Harris
- ↑ RUDIN, Walter; HARRIS, Joe. Fourier Analysis on Groups. New York: Wiley Classics, Wiley-Blackwell, 1990. ISBN 0-471-52364-X. (anglicky)
- ↑ GELBART, Stephen. An Elementary Introduction to the Langlands Program. Bulletin of the American Mathematical Society. 1984, s. 177–219. Dostupné online. DOI 10.1090/S0273-0979-1984-15237-6.
- ↑ Anthony W. Knapp, Group Representations and Harmonic Analysis from Euler to Langlands, Part II, Notices of the AMS, vol 43 (5), May 1996, 537--549
- ↑ James Arthur, Harmonic Analysis and Group Representations, Notices of the AMS, vol 47 (1), 26--34
- ↑ a b VARADARAJAN, V. S. An Introduction to Harmonic Analysis on Semisimple Lie Groups. New York: Cambridge University Press, 1999. ISBN 978-0521663625. (anglicky)
- ↑ Lang 2002, Kapitola VI (konkrétní příklady například na str. 273)
- ↑ Lang, 2002, str. 292 (Theorem VI.7.2)
- ↑ Lang 2002, str. 273
- ↑ HUNGERFORD, Thomas W. Algebra. [s.l.]: Springer, 1996. 502 s. ISBN 9780387905181. S. 103. (anglicky)
- ↑ ROTMAN, Joseph J. Galois theory. [s.l.]: Birkhäuser, 1998. 157 s. ISBN 9780387985411. S. 83-84. (anglicky)
- ↑ The MacTutor History of Mathematics archive, Marie Ennemond Camille Jordan
- ↑ POINCARÉ, Henri. Analysis Situs. Journal de l'École Polytechnique ser 2. 1895, s. 1–123..
- ↑ HATCHER, Allen. Algebraic topology. [s.l.]: Cambridge University Press, 2001. 556 s. Dostupné online. ISBN 978-0521795401. S. 340. (anglicky)
- ↑ SPANIER, Edwin Henry. Algebraic topology. [s.l.]: Springer, 1994. ISBN 9780387944265. S. 371. (anglicky)
- ↑ BROWN, Edgar H. Finite Computability of Postnikov Complexes. The Annals of Mathematics. 1957, s. 1–20. Dostupné online.
- ↑ Hatcher, kap. 2,3
- ↑ HU, Sze-Tsen. Homotopy theory. [s.l.]: Academic Press, 1959. 347 s. ISBN 9780123584502. S. 1-4. (anglicky)
- ↑ Hu, str. 4
- ↑ Hatcher, str. 31
- ↑ Hatcher, str. 126
- ↑ WELSH, Dominic. Codes and cryptography. Oxford: Clarendon Press, 1989. ISBN 978-0-19-853287-3. (anglicky)
- ↑ KUGA, Michio. Galois' dream: group theory and differential equations. Boston: Birkhäuser Boston, 1993. ISBN 978-0-8176-3688-3. S. 105-113. (anglicky)
- ↑ NEUKIRCH, Jürgen. Algebraic Number Theory. Berlin: Springer, 1999. ISBN 978-3-540-65399-8. Kapitola §I.12, I.13. (anglicky)
- ↑ SERESS, Ákos. An introduction to computational group theory. Notices of the American Mathematical Society. 1997, s. 671–679. Dostupné online..
- ↑ Landin, str. 67
- ↑ Landin, str. 83
- ↑ Landin, str. 126
- ↑ Landin, str. 110
- ↑ MORANDI, Patrick. Field and Galois theory. [s.l.]: Springer, 1996. 281 s. ISBN 9780387947532. S. 247. (anglicky)
- ↑ ARTIN, Michael. Algebra. [s.l.]: Prentice Hall, 1991. 618 s. ISBN 9780130047632. Kapitola 6, Theorem 6.1.14. (anglicky)
- ↑ BESCHE, Hans Ulrich; EICK, Bettina; O'BRIEN, E. A. The groups of order at most 2000. Electronic Research Announcements of the American Mathematical Society. 2001, s. 1–4. Dostupné online. DOI 10.1090/S1079-6762-01-00087-7.
- ↑ Lang, 2002, §I. 3, str. 22
- ↑ ASCHBACHER, Michael. The Status of the Classification of the Finite Simple Groups. Notices of the American Mathematical Society. 2004, s. 736–740. Dostupné online..
- ↑ GARNIER, Rowan; TAYLOR, John. 100% Mathematical Proof. [s.l.]: John Wiley & Sons, 1996. ISBN 0 471 96198 1. str. 12.
- ↑ RONAN, Mark. Symmetry and the Monster: The Story of One of the Greatest Quests of Mathematics. [s.l.]: Oxford University Press, 2007. ISBN 978-0-19-280723-6.
- ↑ HIGGINS, Philip J. Introduction to topological groups. London: CUP Archive, 1974. 109 s. ISBN 9780521205276. Kapitola 2, s. 16. (anglicky)
- ↑ HUSAIN, Taqdir. Introduction to topological groups. [s.l.]: Saunders, 1966. 218 s. S. 101. (anglicky)
- ↑ NEUKIRCH, Jürgen. Algebraic Number Theory. Berlin: Springer, 1999. 571 s. ISBN 978-3-540-65399-8. (anglicky)
- ↑ SHATZ, Stephen S. Profinite groups, arithmetic, and geometry. [s.l.]: Princeton University Press, 1972. ISBN 978-0-691-08017-8. (anglicky)
- ↑ MILNE, James S. Étale cohomology. [s.l.]: Princeton University Press, 1980. ISBN 978-0-691-08238-7. (anglicky)
- ↑ WARNER, Frank Wilson. Foundations of differentiable manifolds and Lie groups. [s.l.]: Springer, 1971. 272 s. ISBN 9780387908946. S. 82. (anglicky)
- ↑ BOREL, Armand. Linear algebraic groups. [s.l.]: Springer, 1991. 288 s. ISBN 978-0-387-97370-8. S. 29. (anglicky)
- ↑ HARRIS, Joe; FULTON,, William. Representation theory: a first course. [s.l.]: Springer, 1991. 551 s. ISBN 9780387974958. Kapitola II.8. (anglicky)
- ↑ CORNWEL, J. F. Group theory in physics: an introduction. [s.l.]: Academic Press, 1997. 349 s. ISBN 9780121898007. S. 135. (anglicky)
- ↑ HUMPHREYS, James E. Introduction to Lie algebras and representation theory. [s.l.]: Birkhäuser, 2000. 172 s. ISBN 9780387900537. Kapitola III.11. (anglicky)
- ↑ ONISHCHIK, A. L.; VINBERG, Ėrnest Borisovich. Lie groups and Lie algebras III. [s.l.]: Springer, 1994. 248 s. ISBN 9783540546832. Kapitola 4.1, 4.2. (anglicky)
- ↑ GOLDSTEIN, Herbert. Classical Mechanics. [s.l.]: Addison-Wesley Publishing, 1980. ISBN 0-201-02918-9. S. 588–596. (anglicky)
- ↑ WEINBERG, Steven. Gravitation and Cosmology. New York: John Wiley & Sons, 1972. ISBN 978-0-471-92567-5. S. 25-29. (anglicky)
- ↑ EL NASCHIE, M.S. String theory, exceptional Lie groups hierarchy and the structural constant of the universe. Chaos, Solitons & Fractals. 2008, roč. 35, s. 7-12. Dostupné online.
- ↑ MAC LANE, Saunders. Categories for the Working Mathematician. Berlin, New York: Springer, 1998. ISBN 978-0-387-98403-2. (anglicky)
- ↑ DENECKE, Klaus; WISMATH, Shelly L. Universal algebra and applications in theoretical computer science. London: CRC Press, 2002. ISBN 978-1-58488-254-1. (anglicky)
- ↑ DUDEK, W.A. On some old problems in n-ary groups. Quasigroups and Related Systems. 2001, s. 15–36. Dostupné online.
Literatura
Česká
- ALEXANDROV, Pavel Sergejevič. Úvod do teorie grup. Překlad M. Volf. [s.l.]: Moskva: Mir, 1985. 120 s.
- BOČEK, Leo; ŠEDIVÝ, Jaroslav. Grupy geometrických zobrazení. Praha: Státní pedagogické nakladatelství, 1979. 213 s.
- DRÁPAL, Aleš. Teorie grup (základní aspekty). Praha: Karolinum, 2000. 207 s. ISBN 80-246-0162-1.
- LIVIO, Mario. Neřešitelná rovnice. [s.l.]: Argo, Dokořán, 2008. 320 s. ISBN 978-80-7363-150-5.
- LITZMAN, Otto; SEKANINA, Milan. Užití grup ve fyzice. Praha: Academia, 1982. 276 s.
- PROCHÁZKA, Ladislav, a kol. Algebra. Praha: Academia, 1990. 560 s. ISBN 80-200-0301-0. Kapitola III..
- PROCHÁZKA, Ladislav. Rozšíření grup a grupy krystalografické. [s.l.]: Academia, 2001. 119 s. ISBN 9788024604060.
- RACHŮNEK,, Jiří. Grupy a okruhy. Olomouc: Univerzita Palackého v Olomouci, 2005. 106 s. ISBN 9788024409986.
Anglická
- CORNWELL, J. F. Group theory in physics: an introduction. [s.l.]: Academic Press, 1997. 349 s. ISBN 9780121898007.
- LESK, Arthur M. Introduction to symmetry and group theory for chemists. [s.l.]: Springer, 2004. 122 s. ISBN 9781402021503.
- MCWEENY, Roy. Symmetry: an introduction to group theory and its applications. [s.l.]: Courier Dover Publications, 2002. 248 s. ISBN 9780486421827.
- MILLER, Willard. Symmetry groups and their applications. [s.l.]: Academic Press, 1972. 432 s. ISBN 9780124974609.
- STERNBERG, Shlomo. Group theory and physics. [s.l.]: Cambridge University Press, 1995. 444 s. ISBN 9780521558853.
Externí odkazy
České
- Motl L., Zahradník M., Pěstujeme lineární algebru, kapitola Grupa (skripta)
- Martin Kuřil, Základy teorie grup (učební text)
- Pavel Růžička, Elementární teorie grup
- Lucie Horálková, Grupy symetrií, bakalářská práce
- Jakub "šnEk" Opršal, Rubikova teorie grup
- Grupa na stránkách Krystalografické společnosti
Anglické
- Knihy o teorii grup na e-books, volně ke stažení
- Frank W. K. Firk (Yale University), Introduction to Groups, Invariants & Particles, volně ke stažení
- The Small Groups library, popis grup malých řádů
- en:List of finite simple groups, věta o klasifikaci konečných jednoduchých grup na anglické wikipedii
- John Jones, Group Tables and Subgroup Diagrams
- Lie, program na počty související s reprezentacemi Lieových grup
- Popis malých grup do řádu 30
- Grupa na MathWorld































































![{\displaystyle \scriptstyle (\mathbb {Z} [i],+)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30c99073ff54858f45a7ebccb62612feb4da74e1)









