Přímka
Přímka je jednorozměrný základní geometrický útvar.
Lze ji popsat jako nekonečně tenkou, dvoustranně nekonečně dlouhou, dokonale rovnou křivku (pojem křivka v matematice zahrnuje i „rovné křivky“), tedy křivku s nekonečně velkým poloměrem zakřivení. V euklidovské geometrii pro každé dva body existuje právě jedna přímka, která oběma prochází. Tato přímka obsahuje nejkratší spojnici mezi dotyčnými body, úsečku z jednoho bodu do druhého.
Z fyzikálního hlediska je přímka trajektorie fotonu neovlivněného gravitací.
Speciální případ přímky je osa.
Znázornění a značení[editovat | editovat zdroj]
Přímka se znázorňuje rovnou čarou, označuje se malým písmenem, např. . Přímka procházející dvěma body bývá také značena .
Znázornění:
Algebraický zápis[editovat | editovat zdroj]
Přímku v rovině lze algebraicky popsat pomocí lineárních rovnic nebo lineárních funkcí.
Tento intuitivní koncept přímky lze formalizovat několika způsoby. Jestliže je geometrie postavena axiomaticky (jako v Eukleidových Základech a později ve Foundations of Geometry Davida Hilberta), potom přímky nejsou vůbec definovány, nýbrž axiomaticky charakterizovány svými vlastnostmi. „Vše, co splňuje axiomy pro přímku, je přímka.“ Zatímco Eukleidés definoval přímku jako „délku bez šířky“, ve svých pozdějších vývodech tuto mlhavou definici nepoužíval.
V eukleidovském prostoru Rn (a analogicky ve všech ostatních vektorových prostorech) definujeme přímku L jako podmnožinu ve tvaru
kde a a b jsou vektory v Rn a b je nenulové. Vektor b udává směr přímky a a je bod na přímce. Tutéž přímku lze definovat pomocí různých kombinací a a b.
Rovinná přímka[editovat | editovat zdroj]
V R2 je každá přímka L popsaná lineární rovnicí, která může být zadána v různých tvarech.
Směrnicová rovnice přímky[editovat | editovat zdroj]

Směrnicová rovnice přímky má tvar
- ,
kde je tzv. směrnice přímky, přičemž je orientovaný úhel s vrcholem v průsečíku přímky a první souřadnicové osy, jehož rameny jsou (kladně orientovaná) první osa souřadnicové soustavy a přímka, a je tzv. úsek (vytnutý přímkou) na ose , což je druhá souřadnice průsečíku přímky s osou .
Pro představuje rovnice přímky rostoucí funkci, pro jde o funkci klesající. Pro je přímka rovnoběžná s osou . Je-li , pak přímka prochází počátkem .
Přímku rovnoběžnou s osou nelze směrnicovou rovnicí vyjádřit.
Úseková rovnice přímky[editovat | editovat zdroj]
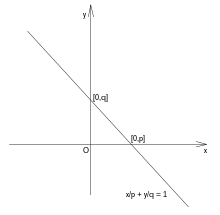
Úseková rovnice přímky má tvar
- ,
kde je úsek (vytnutý přímkou) na ose a je úsek (vytnutý přímkou) na ose .
Přímku rovnoběžnou s osou nebo nelze úsekovou rovnicí vyjádřit.
Normálová rovnice přímky[editovat | editovat zdroj]

Normálovou rovnici přímky lze zapsat ve tvaru
- ,
kde představuje vzdálenost počátku soustavy souřadnic od přímky a je velikost orientovaného úhlu, jehož rameno je první kladná poloosa souřadné soustavy a druhé rameno je polopřímka s počátkem v vedená kolmo k přímce.
Členy a představují složky jednotkového vektoru kolmého k přímce.
Obecná rovnice přímky[editovat | editovat zdroj]
Obecná rovnice přímky v rovině je speciálním případem obecné rovnice nadroviny a má tvar
- ,
kde jsou konstanty, přičemž nebo .
Pro je přímka rovnoběžná s osou , pro je přímka rovnoběžná s osou . Pro prochází přímka počátkem.
Porovnáním obecné a normálové rovnice lze určit význam konstant . Konstanty určují vektor , který je kolmý k přímce. Parametr pak souvisí se vzdáleností přímky od počátku souřadné soustavy.
Obecnou rovnici přímky lze převést na rovnici směrnicovou, pokud zavedeme , pro . Zavedeme-li , pro , pak můžeme obecnou rovnici převést na úsekový tvar. Převedením obecné rovnice přímky do normálového tvaru získáme normálovou rovnici přímky ve tvaru
Důležité vlastnosti takto definovaných přímek jsou jejich sklon, průsečík s osou x a průsečík s osou y. Excentricita přímky je nekonečno.
Parametrické vyjádření přímky[editovat | editovat zdroj]
Parametrické vyjádření přímky je definováno vztahem: a v rovině je tedy dáno rovnicemi
kde je libovolný bod přímky, jsou konstanty určující směrnici přímky, tedy vektor je směrovým vektorem přímky a je proměnný parametr. Alespoň jedna z konstant musí být nenulová.
Vektorová rovnice přímky[editovat | editovat zdroj]
Vektorová rovnice přímky má tvar
kde je rádiusvektor procházející všemi body přímky, je rádiusvektor jednoho z bodů přímky, je vektor určující směr přímky a je proměnný parametr.
Vektorový zápis tedy představuje přehlednější zápis parametrického tvaru rovnice přímky.
Polární rovnice přímky[editovat | editovat zdroj]
V polárních souřadnicích lze přímku vyjádřit jako
- ,
kde je vzdálenost přímky od počátku a je velikost orientovaného úhlu s vrcholem v počátku, jehož první rameno tvoří polární osa a druhé rameno polopřímka kolmá k přímce s počátkem v O.
Rovnice přímky určené bodem[editovat | editovat zdroj]
Rovnice přímky se směrnicí procházející bodem je
Rovnice přímky procházející dvěma danými body a , kde , má tvar
neboli
Předchozí rovnice bývá také vyjadřována ve formě determinantu
Tuto rovnici lze využít jako podmínku k určení, zda tři body leží na jedné přímce. Tyto body leží na jedné přímce, je-li splněna podmínka
Prostorová přímka[editovat | editovat zdroj]
Přímkou v prostoru se nazývá množina bodů prostoru, které vyhovují rovnici přímky. Rovnici přímky v prostoru lze vyjádřit různými způsoby.
Obecná rovnice přímky[editovat | editovat zdroj]
V R3 lze přímku L definovat jako průsečík dvou rovin, pomocí soustavy jejich lineárních rovnic:
(definici je nutné rozšířit o podmínky pro koeficienty až , které zaručí, že roviny budou různoběžné).
Přímka v prostoru je tedy řešením soustavy rovnic
Ve speciálním případě vyjádříme přímku jako průsečík dvou rovin, z nichž každá je kolmá k některé souřadnicové rovině, např. pro roviny kolmé k a dostaneme
Parametrické rovnice přímky[editovat | editovat zdroj]
Parametrické rovnice přímky v prostoru mají tvar
kde je libovolný bod, kterým přímka prochází, jsou konstanty určující směrnici přímky a je parametr.
Konstanty mohou být vyjádřeny prostřednictvím směrových úhlů jako
Směrové úhly přitom splňují podmínku
Rovnice přímky určené bodem[editovat | editovat zdroj]
Rovnici přímky procházející body lze zapsat jako
Rovnici přímky procházející bodem se směrovými úhly lze zapsat jako
Pokud místo směrových úhlů určíme směrnici přímky parametry , pak lze předchozí vztah přepsat jako
Přímka ve vícerozměrném prostoru[editovat | editovat zdroj]
Přímku lze zavést také v n-rozměrném prostoru.
Parametrické vyjádření[editovat | editovat zdroj]
Přímku v Rn lze také vyjádřit parametricky: přímka procházející bodem se směrovým vektorem je množina bodů , pro které existuje skalár k takový, že
Vektorový tvar[editovat | editovat zdroj]
Místo předchozího parametrického vyjádření lze použít vektorový zápis
Vzájemná poloha bodu a přímky[editovat | editovat zdroj]
Tři nebo více bodů, které leží na téže přímce, se nazývají kolineární.
Leží-li tři (různé) body na jedné přímce, pak vždy leží právě jeden z nich mezi ostatními dvěma. Leží-li bod mezi body a , pak bod označíme jako vnitřní bod úsečky .
Bod ležící na přímce ji dělí na dvě polopřímky. Je-li bod vnitřním bodem jedné z polopřímek, pak pro tuto polopřímku užíváme značení . Opačnou polopřímku k polopřímce značíme .
Vzájemná poloha přímek[editovat | editovat zdroj]
Dvě různé přímky ležící v téže rovině mohou být buď rovnoběžné a nemít žádný společný bod (v eukleidovském prostoru se protínají v nekonečnu), nebo různoběžné a protnout se v právě jednom bodě, průsečíku. Dvě roviny se protínají v nejvýše v jedné přímce, průsečnici. Ve vícerozměrných prostorech ale nemusí ani být rovnoběžné, ani se protínat, a říká se jim mimoběžky.
Pokud jsou si obě přímky rovny, pak říkáme, že jde o přímky splývající (totožné).
Přímku různoběžnou s rovnoběžkami označujeme jako příčku rovnoběžek .
Průnik dvou polopřímek a se nazývá úsečkou a značí .
Některé důležité přímky[editovat | editovat zdroj]
- asymptota – přímka, ke které se limitně blíží daná křivka, zejména graf funkce, pro nezávisle proměnnou rostoucí nade všechny meze,
- číselná osa – přímka s reálnými čísly přiřazenými každému jejímu bodu, užívaná např. jako souřadná osa,
- osa rotace – přímka, kolem níž rotuje (otáčí se) dané těleso nebo vůči které provádíme matematické otáčení tělesa,
- osa symetrie – přímka, ke které lze zrcadlově obrátit geometrický útvar a dostat tak útvar totožný,

- Eulerova přímka,
- Simsonova přímka,
- tečna – přímka dotýkající se křivky nebo plochy, prochází průběžným bodem (bodem dotyku) křivky (plochy) jednostranně, neprotíná ji v něm,
- normála – kolmice k tečně v bodě dotyku křivky, laicky „kolmice ke křivce“,
- kolmice – přímka pravoúhle skloněná k dané přímce nebo rovině,
- těžnice – přímka procházející vrcholem trojúhelníku a středem protilehlé strany, půlící jeho plochu.
Odkazy[editovat | editovat zdroj]
Literatura[editovat | editovat zdroj]
- Marcela Palková a kolektiv: Průvodce matematikou 2, Didaktis, Brno 2007, ISBN 978-80-7358-083-4, str. 8-9
- Šárka Voráčová a kolektiv: Atlas geometrie – Geometrie krásná a užitečná, Academia, Praha 2012, ISBN 978-80-200-1575-4, str. 12
Související články[editovat | editovat zdroj]
- Základní geometrické útvary
- Lineární geometrické útvary
- Vzájemná poloha přímky a kružnice
- Výpočet průsečíku křivek
Externí odkazy[editovat | editovat zdroj]
 Obrázky, zvuky či videa k tématu přímka na Wikimedia Commons
Obrázky, zvuky či videa k tématu přímka na Wikimedia Commons  Slovníkové heslo přímka ve Wikislovníku
Slovníkové heslo přímka ve Wikislovníku










































![{\displaystyle A=[x_{0},y_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b3329e1cf12b53aaf1ac606c7414d885ea17139)










![{\displaystyle [x_{0},y_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d3caa55d3f5b0f9ed69a4352c251877397060fb)

![{\displaystyle [x_{1},y_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/803462d0ee7e478032128b2efc576d4dd7b821e3)
![{\displaystyle [x_{2},y_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32c6a746d50d795c9b47d483370a561d9b9ea276)




![{\displaystyle [x_{1},y_{1}],[x_{2},y_{2}],[x_{3},y_{3}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7a573c6737fe176ae1ae5571e8a32bdc173d6d0)













![{\displaystyle [x_{0},y_{0},z_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/783963bcced1f79ece185af36af724239002afaa)





![{\displaystyle [x_{1},y_{1},z_{1}],[x_{2},y_{2},z_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca6ecc8e08f8f8570262ecc1329562b3ef5f9b65)

![{\displaystyle [x_{1},y_{1},z_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0c388d9b95453e0fc82d4267fbdc0fd13cf5314)


















