Limita

Limita je matematická konstrukce vyjadřující, že se hodnoty zadané funkce nebo posloupnosti blíží libovolně blízko k nějakému bodu. Právě tento bod je pak označován jako limita. Tato skutečnost se u funkcí zapisuje a u posloupností .
Dle toho, zda se uvažuje o funkci nebo o posloupnosti, hovoříme o limitě funkce nebo limitě posloupnosti. Pojem limity lze definovat na reálných číslech, obecnější definice má smysl na libovolném metrickém prostoru a ještě obecnější definice na libovolném topologickém prostoru. Tam, kde má smysl více definic, jsou tyto definice ekvivalentní (například reálná čísla jsou metrickým i topologickým prostorem).
Limita funkce[editovat | editovat zdroj]
Číslo je limitou funkce v bodě , jestliže pro libovolné existuje takové, že pro každé takové, že ( leží v prstencovém okolí bodu ) platí .
Limita posloupnosti[editovat | editovat zdroj]
Číslo je limitou posloupnosti , jestliže pro libovolné existuje takové, že pro každé platí .
Limita v metrickém prostoru[editovat | editovat zdroj]
Prvek metrického prostoru s metrikou je limitou posloupnosti jeho prvků , právě když platí .
Limita v topologickém prostoru[editovat | editovat zdroj]
Limita zobrazení mezi topologickými prostory a je v bodě definována jako takové, že pro každé okolí bodu existuje okolí bodu takové, že implikuje .
Dalším zobecněním limity posloupnosti, funkce i zobrazení jsou limity topologických sítí[1]. Limita zobrazení nebo topologické sítě může být v obecném topologickém prostoru víceznačná. Platí však, že v Hausdorffově prostoru je tato limita jednoznačná, tj. každé zobrazení či topologická síť má nejvýše jednu limitu.
Nevlastní limita v nevlastním bodě[editovat | editovat zdroj]
Pokud pro libovolné číslo lze nalézt prvek posloupnosti, počínaje kterým jsou všechny hodnoty posloupnosti větší než , říkáme, že posloupnost roste nade všechny meze neboli že má nevlastní limitu . Obdobně se definuje nevlastní limita .
Pokud pro libovolné číslo lze nalézt okolí bodu , ve kterém má funkce hodnotu větší než , říkáme, že v okolí bodu funkce roste nade všechny meze neboli že má nevlastní limitu . Obdobně se definuje nevlastní limita .
Limitou tedy může být nejen reálné číslo, ale i nebo (rozšířené reálné číslo).
Pokud se hodnoty limity neliší od čísla o více než libovolné číslo , má funkce v nevlastním bodě vlastní limitu . Pokud jsou hodnoty limity větší než libovolné číslo , má funkce v nevlastním bodě nevlastní limitu . Obdobným způsobem lze definovat limitu v nevlastním bodě .
V každém z nevlastních bodů nebo může mít funkce vlastní limitu, nevlastní limitu nebo limita nemusí existovat. Příkladem funkce, která nemá limitu v žádném z bodů nebo , je funkce sinus.
Příklady[editovat | editovat zdroj]
-
Graf funkce . Je vidět, že tato funkce má limitu 1 v bodě nula.
-
Graf funkce . Je vidět, že tato funkce nemá limitu v bodě nula a má vlastní limity 0 v .
-
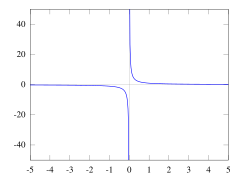
Graf funkce . Je vidět, že tato funkce má nevlastní limitu v bodě nula a má vlastní limity 0 v .
- Funkce není v nule definovaná, ale má v ní limitu 1[pozn. 1] (vlastní limita ve vlastním bodě) a v má limitu 0 (vlastní limita v nevlastním bodě).
- Funkce ani v nule limitu nemají. Totéž platí i o funkcích či , ovšem ty mají alespoň jednostranné limity: jejich pravostranná limita je a levostranná .
- Funkce a mají v nule limitu (nevlastní limita ve vlastním bodě).
- Funkce má v nule limitu 0 a v limitu nemá. Obě tato tvrzení platí i o funkci .
- Funkce má v limitu 0 (vlastní limita v nevlastním bodě) a v limitu .
Poznámky[editovat | editovat zdroj]
- ↑ To lze intuitivně zdůvodnit tak, že funkce sin x má v okolí nuly „velmi podobný“ průběh, jako funkce f(x) = x; proto se jejich poměr blíží k jedné. (L'Hospitalovo pravidlo)
Reference[editovat | editovat zdroj]
- ↑ Michael C. Gemignani, Elementary topology, Courier Dover Publications, 1990 (strana 122, def. 3)
Související články[editovat | editovat zdroj]
Externí odkazy[editovat | editovat zdroj]
 Obrázky, zvuky či videa k tématu limita na Wikimedia Commons
Obrázky, zvuky či videa k tématu limita na Wikimedia Commons  Encyklopedické heslo Limita v Ottově slovníku naučném ve Wikizdrojích
Encyklopedické heslo Limita v Ottově slovníku naučném ve Wikizdrojích