Axiomatická teorie množin

Axiomatická teorie množin je označení pro teorii, která formalizuje vlastnosti množin takovým způsobem, aby bylo možné pomocí množin zkonstruovat všechny matematické objekty, takže dokazatelná tvrzení této teorie budou přesně odpovídat všem platným matematickým výsledkům ze všech oblastí matematiky (algebra, diferenciální rovnice, geometrie, teorie pravděpodobnosti i všechny ostatní).[zdroj?]
Hlavní význam takových teorií je v tom, že staví na velmi solidní základ pojem „dokazatelné matematické tvrzení“ a tedy poskytují užitečné vodítko při ověřování, zda nějaký matematický důkaz je korektní.[zdroj?]
Nejpoužívanější axiomatická teorie množin je jednak Zermelova-Fraenkelova teorie množin (značení ZF) a dále ZF s přidaným axiomem výběru (ta se značí ZF+AC nebo ZFC). ZFC je všeobecně uznávána jako teorie, která přesně popisuje platné matematické pravdy, tj. matematická věta je pokládána za pravdivou, právě když je dokazatelná v ZFC (dokazatelnost ovšem nelze snadno ověřit, neboť v každém okamžiku existuje mnoho pravdivých hypotéz, které ještě nebyly dokázány nebo ani vysloveny).[zdroj?]
Aplikace Gödelových vět o neúplnosti na axiomatickou teorii množin přináší vhledy na podstatu a filosofii matematiky, neboť z ní vyplývá, že sebelepší axiomatika teorie množin bude vždy obsahovat nerozhodnutelná tvrzení (množinu všech matematických pravd nelze popsat žádnou soustavou axiomů) a že pokud teorie, kterou chceme používat k popisu všech matematických pravd, je bezesporná, nelze tuto bezespornost dokázat.[zdroj?]
Důvod vzniku[editovat | editovat zdroj]
K převážné většině matematických konstrukcí (včetně pokročilých, jako je úplný obal metrického prostoru) stačí intuitivní (naivní) teorie množin, v níž intuitivně pracujeme s množinami jako se souhrny objektů. Tento přístup však vede k rozporům, pokud pracujeme s „příliš velkými“ množinami (nejznámější z těchto sporů je Russelův paradox). Vzato do důsledků, naivní teorie množin je sporná a proto v ní lze dokázat cokoli (např. že 1+1=42).
V reakci na tyto rozpory vznikla axiomatická teorie množin, která staví dokazatelnost matematických pravd na pevný základ. Její hlavní přednosti oproti naivní teorii jsou tyto:
1. Neumožňuje Russelův paradox (a další paradoxy naivní teorie množin) tím, že velké souhrny objektů (například „souhrn všech množin“) v ní nejsou pokládány za množiny, nýbrž jsou nazývány vlastními třídami a pracuje se s nimi jinak.[zdroj?]
2. Nepředpokládá nic kromě přesně vyjmenovaných axiomů (odtud název „axiomatická“). Ani tak samozřejmé skutečnosti, jako že existuje prázdná množina (nebo že k množinám a, b existuje i množina {a,b}) není dovoleno předpokládat, dokud to není dokázáno z axiomů anebo samo není axiomem.
Predikátová logika dává návod, jak prohledáváním nekonečného stromu ověřit dokazatelnost tvrzení z dané množiny axiomů.[zdroj?] Existence soustavy axiomů, z nichž plyne každé matematické tvrzení, tedy umožňuje algoritmicky rozhodnout o pravdivosti jakékoli matematické hypotézy (tento algoritmus se nezastaví, pokud je tato hypotéza nerozhodnutelná z axiómů ZFC). To je sice v praxi nepoužitelné, protože počet větví stromu je astronomicky velký, ale přesto je ZFC užitečným vodítkem při diskuzi, zda nějaký argument lze nazvat platným matematickým důkazem.
Proč množiny?[editovat | editovat zdroj]
Při konstrukci teorie, která má obsáhnout celou matematiku, není možné do ní přidat všechny druhy objektů – například přidat predikát „tento objekt univerza je přirozené číslo“ (podobně, jako GB má predikát „tento objekt je množina“) a vložit axiomy, které chování přirozených čísel popisují (např. Peanovy axiomy).
Při takovém přístupu by se množina predikátů a axiomů neustále rozrůstala, například po objevení komplexních čísel, hyperkomplexních čísel apod. S každým rozšířením by se musely znovu dokazovat výsledky o teorii dokázané (například to, že nějaké tvrzení je v této teorii nezávislé).[zdroj?][pozn 1]
Proto je zvolen opačný přístup: axiomy popisují vlastnosti skupiny co nejjednodušších objektů, které stačí ke zkonstruování celé matematiky. Ukázalo se, že k tomuto účelu nejlépe slouží množiny; z těch lze zkonstruovat přirozená čísla, reálná čísla, funkce, přímky, topologické prostory atd.
Konstrukce objektů[editovat | editovat zdroj]
Jelikož cílem ZF je popsat jedinou soustavou axiomů celou matematiku, není možné postupovat tak, že zavedeme pojem např. „přirozené číslo“ a vložíme axiomy o tom, jaké vlastnosti přirozená čísla mají. V takovém případě bychom museli rozšířit množinu axiomů pokaždé, když je v matematice objeven další důležitý pojem (reálné číslo, funkcionál, kategorie...)
Proto ZF vychází z předpokladu, že všechny matematické objekty jsou množiny, a její axiomy poskytují možnost z množin konstruovat množiny složitější. Prvek množin tedy mohou být opět jen množiny.
Matematické objekty, se kterými chceme pracovat, pak ztotožníme s vhodnými množinami – víme, jaké vlastnosti očekáváme od přirozených čísel (například že ke každému číslu existuje číslo o jedničku větší), a proto zvolíme množiny, které odpovídající vlastnost mají.
Uspořádané dvojice[editovat | editovat zdroj]
Symbol (a, b) pokládáme za zkratku pro {{a}, {a, b}} .Tato definice splňuje základní vlastnost, kterou od uspořádaných dvojic čekáme:
- (a, b) = (c, d) právě když a = c a zároveň b = d.
Přirozená čísla[editovat | editovat zdroj]
- Číslo 0 ztotožníme s prázdnou množinou
- Číslo 1 ztotožníme s množinou
- Číslo 2 ztotožníme s množinou
- Číslo 3 ztotožníme s množinou
- Obecně
Formálně: Množinu přirozených čísel definujeme jako průnik všech množin, které obsahují prázdnou množinu a s každým svým prvkem obsahují i množinu .
Množinu přirozených čísel (včetně nuly) značíme .
Celá čísla[editovat | editovat zdroj]
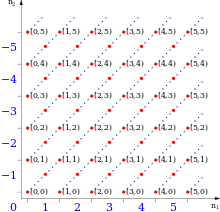
Máme-li definovaná přirozená čísla, pak by se mohlo zdát přirozené reprezentovat záporné číslo jako . To však nelze, protože pro některá přirozená čísla by mohlo platit .
Je však možné reprezentovat přirozená čísla (pro ) jako a záporná čísla (pro ) jako . Tato definice se nepoužívá, protože by definice sčítání, násobení apod. byla složitější, než u definice následující:
Idea je reprezentovat celé číslo nekonečnou množinou takových dvojic , že jsou přirozená čísla splňující . Například
Formálně: Množina celých čísel je definována jako rozklad (tedy množina všech tříd ekvivalence) kartézského součinu x podle ekvivalence:
- ~ právě když .
Máme-li definované sčítání a násobení pro přirozená čísla, definujeme je pro celá čísla takto: vyberme libovolný prvek (tzv. reprezentant) a čísel, které chceme sečíst. Výsledkem bude třída ekvivalence, která obsahuje dvojici (tato třída nezávisí na volbě reprezentantů):
- Pro sčítání:
- Pro násobení:
Vzoreček pro násobení lze snadno odvodit roznásobením vztahu
Podobně se postupuje i u dalších matematických operací.
Za pozornost stojí i skutečnost, že totéž číslo (například 2) je reprezentováno jinak jako přirozené číslo než jako celé číslo. Množina přirozených čísel tedy formálně není podmnožinou množiny celých čísel. S podobným jevem se v teorii množin setkáváme velmi často; tento přístup je volen proto, abychom nemuseli změnit reprezentaci množiny, pokud konstruujeme její rozšíření – například kdyby komplexní čísla a kvaterniony (což jsou oboje rozšíření reálných čísel) byly objeveny až poté, co byla ustálena konvence, jak reálná čísla v teorii množin reprezentovat.
Racionální čísla[editovat | editovat zdroj]
Každé racionální číslo lze zapsat nekonečně mnoha způsoby jako zlomek, např.:
- 3/2 = 6/4 = 300 / 200 = -300 / -200.
Racionální číslo budeme tedy reprezentovat množinou všech takovýchto dvojic .
Formálně: Množina racionálních čísel je definována jako rozklad (tedy množina všech tříd ekvivalence) množiny
podle ekvivalence
- ~ právě když .
V této definici značí množinu celých čísel definovanou výše a zápis se týká nuly jako celého čísla, což je formálně jiný objekt, než nula jako přirozené číslo.
Definice sčítání, násobení apod. odvodíme podobným způsobem jako u celých čísel.
Reálná čísla[editovat | editovat zdroj]
Reálná čísla je možno definovat několika způsoby, například ztotožnit jejich množinu s množinou všech Dedekindových řezů.
Gödelovy věty a nedokazatelná tvrzení[editovat | editovat zdroj]
Gödelovy věty o neúplnosti říkají, že je-li nějaká predikátová teorie bezesporná, rekurzivně axiomatizovatelná a dokazuje základní aritmetické pravdy, pak není úplná a neumí dokázat svoji bezespornost.
V každé teorii, kterou chceme pokládat za popis všech matematických pravd, musí být dokazatelné základní aritmetické pravdy a měl by existovat algoritmus, kterým ověříme, zda dané tvrzení je axiomem; bez takového algoritmu je teorie nepoužitelná k praktickým účelům.[pozn 2]
Z toho plyne, že je-li tato teorie bezesporná, pak pro ni platí obě Gödelovy věty o neúplnosti a její bezespornost není nikdy možné dokázat.[pozn 3] V její bezespornost matematická komunita pevně věří, protože spor nebyl objeven přes téměř celé století, kdy je tato teorie používána. Pro ZFC, která je běžně přijímána jako popis všech matematických pravd, jsou tedy dvě možnosti:
- ZFC je bezesporná, potom nikdy nebude objeven důkaz sporu i důkaz bezespornosti.
- ZFC je sporná; pokud bude objeven důkaz její bezespornosti, Gödelova druhá věta o neúplnosti dá návod, jak zkonstruovat důkaz sporu.
Dopad na filosofii matematiky[editovat | editovat zdroj]
Výše uvedené úvahy nevyužívaly specifické vlastnosti ZFC. Platí o každé rekurzívně spočetné teorii, kterou přijímáme jako popis všech matematických pravd a která umí dokázat základní pravdy aritmetiky (poslední podmínka v zásadě plyne z předposlední).
Z toho plyne, že výše uvedené „vady“ ZFC (její neúplnost a nemožnost ověřit její bezespornost) nelze napravit vhodnější volbou jejích axiomů; není tedy možný Hilbertův program. Matematické pravdy tedy nikdy nebudou plně popsány soustavou axiómů.
Bezespornost ZFC je možno snadno dokázat v nějaké silnější teorii (např. Kelleyova-Morseova teorie s axiómem výběru), ovšem to nemá žádnou váhu pro ověření, že je skutečně bezesporná. Kdybychom si byli jisti bezesporností KM+AC, nemuseli bychom ověřovat bezespornost ZFC, která z ní plyne. A pokud si nejsme jisti ani bezesporností KM+AC, tím méně můžeme spoléhat, že každé tvrzení v ní dokazatelné je pravdivé (což je podstatně silnější tvrzení: například PA s přidaným axiomem „PA je sporná“ je bezespornou teorií).
Nerozhodnutelná tvrzení v teorii množin mají nejen akademický význam, ale týkají se i „praktičtějších“ oblastí matematiky, jako je Matematická analýza (příkladem je Hypotéza kontinua). Bez axiomu výběru je nerozhodnutelná i řada zcela fundamentální faktů pro práci v matematice, například zda je každá funkce Lebesgueovsky integrovatelná a zda je kartézský součin neprázdných množin vždy neprázdný.
Historie[editovat | editovat zdroj]

Axiomatická teorie množin se vyvinula během dvacátého století z naivní teorie množin, kterou zavedli Georg Cantor a další.
Naivní teorie množin[editovat | editovat zdroj]
Naivní teorie množin vznikla z nutnosti popsat objekty, se kterými pracovala matematická analýza i v jiných matematických disciplínách.
Prvním vážným pokusem o přesný popis těchto objektů byla práce Bernarda Bolzana, jenž zavedl pojem množina a zkoumal vlastnosti nekonečných množin. Na toto téma napsal knihu Paradoxy nekonečna (Paradoxien des Unendlichen), která byla vydána až po jeho smrti.
Opravdovým zakladatelem teorie množin je Georg Cantor, který zavedl pojmy jako potenční množina, ordinál či kardinál. Též dokázal existenci nespočetných množin. K tomu použil zcela nový důkazní prostředek, dnes nazývaný Cantorova diagonální metoda. Později dokázal takzvanou Cantorovu větu tvrdící, že ke každé množině existuje množina o větší mohutnosti – její potenční množina. Používal tuto definici množiny: „Množinou A rozumíme souhrn určitých a rozlišitelných objektů x existujících v naší mysli. Těmto objektům říkáme prvky množiny A.“.[1] Tato teorie dosáhla vynikajících výsledků, avšak na přelomu devatenáctého a dvacátého století se v ní objevili antinomie (takzvané paradoxy naivní teorie množin; viz níže).
Paradoxy naivní teorie množin a počátky axiomatické teorie množin[editovat | editovat zdroj]
Na přelomu 19. a 20. století byly v naivní teorii množin objeveny antinomie (takzvané paradoxy naivní teorie množin). První se týkaly pouze velmi velkých souborů, jako je množina všech ordinálních čísel (Burali-Fortiho paradox) anebo množina všech množin (Cantorův paradox). Těmto antinomiím se nepřikládal velký význam, neboť se předpokládalo, že zpřesněním práce s tak velkými soubory se odstraní.
Opravdovým problémem se ukázal Russellův paradox, týkající se množiny, která je definována jednoduchou formulí. Russellův paradox se dá popsat takto: „Mějme množinu všech množin, které nejsou prvky samy sebe. Je tato množina svým prvkem? Obě možné odpovědi vedou ihned ke sporu.
V následujících letech se objevilo ještě několik obdobných problémů; například Richardův paradox týkající se diagonální metody a sémantiky obecného jazyka.
Počátky axiomatické teorie množin[editovat | editovat zdroj]
V roce 1908 Ernst Zermelo v článku Untersuchungen über die Grundlagen der Mengenlehre (česky: Zkoumání základů teorie množin) popsal teorii množin s axiomem extenzionality, axiom dvojice, axiom potenční množiny, axiom sumy, axiom nekonečna, axiom výběru a schéma axiomů vydělení.[2] V roce 1917 Dmitrij Mirimanov schéma axiomů vydělení nahradil obecnějším schématem axiomů nahrazení.
Jednotlivé systémy[editovat | editovat zdroj]
Existuje několik různých systémů axiomatizace teorie množin s různou silou a výsledky. Zde je uvedena jen část z nich.
Zermelova-Fraenkelova teorie množin[editovat | editovat zdroj]
Zermelova-Fraenkelova teorie množin je dnes nejužívanější ze systémů axiomatické teorie množin[zdroj?], která je sama o sobě nebo v některých mírných modifikacích (zejména s přidaným axiomem výběru) používána jako základ pro většinu dalších odvětví matematiky včetně algebry a matematické analýzy.[zdroj?] Tento systém nedefinuje třídy, ty jsou jen součástí metajazyka.[zdroj?]
Mezi tvrzení nerozhodnutelná v této teorii patří například axiom výběru[3], hypotéza kontinua[4], Axiom konstruovatelnosti[5] a Suslinova hypotéza[6]. Všechny výsledky tohoto druhu (že něco nejde z axiomů ZFC dokázat) jsou ovšem formulovány s podmínkou „Pokud je ZFC bezesporná“, neboť její bezespornost nelze ověřit.
Je založena na těchto axiomech[7][pozn 4]:
- Axiom extenzionality: Množiny, které mají stejné prvky, se rovnají.
- Schéma axiomů nahrazení: Je-li F(x,y) formule jazyka teorie množin v proměnných x,y, která je navíc zobrazením (tj. pokud F(x,y) a F(x,z), pak y = z) pak každý výrok Pro každou množinu a existuje množina b obsahující právě všechny obrazy prvků množiny a v zobrazení F(x,y) je axiomem ZF.
- Axiom dvojice: Pro každé dvě množiny a,b existuje množina c obsahující právě tyto dvě množiny.
- Axiom sumy: Pro každou množinu a existuje množina b, která obsahuje právě všechny prvky prvků množiny a.
- Axiom potenční množiny: Pro každou množinu a existuje množina b, která obsahuje právě všechny podmnožiny množiny a.
- Axiom nekonečna:
- Axiom fundovanosti:
Zermelova-Fraenkelova teorie množin s axiomem výběru[editovat | editovat zdroj]
Zkratkou ZFC je označována axiomatická soustava teorie množin, kterou tvoří axiomy Zermelo-Fraeneklovy teorie množin a axiom výběru (zkratka AC – z anglického axiom of choice).
Von Neumannova-Bernaysova-Gödelova teorie množin[editovat | editovat zdroj]
Von Neumannova-Bernaysova-Gödelova teorie množin (NBG, též (Von Neumannova)-Gödelova-Bernaysova teorie množin, NGB, GB) se z hlediska své síly příliš neliší od ZF či ZFC – libovolný výrok o množinách je v NBG dokazatelný tehdy a jen tehdy, pokud je dokazatelný v ZF – mluvíme tedy o teorii NBG jako o konzervativním rozšíření teorie ZF (říkáme také, že NBG a ZF jsou ekvikonzistentní).[11][12] Rozdíl mezi oběma teoriemi spočívá v použitém jazyku a v počtu axiomů. NBG jich má konečný počet díky použití vlastních tříd.[11][13]
Na rozdíl od ZFC, jejímž objektem jsou pouze množiny, zatímco třídy tvoří pomocný konstrukt na úrovni metajazyka, v NBG jsou množiny i třídy objektem teorie množin – na množiny jsou však kladena (jejich definicí) určitá omezení – jednoduše řečeno množiny jsou právě ty objekty, které jsou prvkem jiného objektu:
- .
Někdy se k axiomům NBG přidává ještě takzvaný axiom výběru či silný axiom výběru. Výsledná teorie se pak značí NBG+AS[zdroj?].
Na rozdíl od ZF neobsahuje (právě díky zavedení tříd jako součásti jazyka teorie množin) NBG nekonečný počet axiomů – nemusí si totiž vypomáhat axiomatickými schématy typu schématu axiomů nahrazení nebo schématu axiomů vydělení.[11]
Je založena na těchto axiomech (malá písmena značí množinové proměnné a velká písmena obecné (třídové) proměnné)[14]:
- axiom definice množiny:
- axiom existence množiny:
- axiom extenzionality pro třídy:
- schéma existence tříd: kde je formule v níž jsou kvantifikovány pouze množinové proměnné
- axiom dvojice:
- axiom nahrazení:
Kelleyova-Morseova teorie množin[editovat | editovat zdroj]
Kelleyova-Morseova teorie množin (označovaná též KM) je teorie silnější než jsou klasické axiomatizace Zermelova-Fraenkelova (ZF) a Von Neumannova-Gödelova-Bernaysova (NGB).[15] V KM je dokazatelná (formální) konzistence ZF[zdroj?].
Axiomatizace KM je velmi podobná axiomatizaci GB, liší se pouze ve schématu existence tříd, kde (na rozdíl od GB) připouští existenci třídy odpovídající libovolné formuli. Tato zdánlivě drobná odlišnost je však příčinou toho, že KM je nesrovnatelně silnější teorií než GB i ZF.[zdroj?]
Je založena na těchto axiomech (malá písmena značí množinové proměnné a velká písmena obecné (třídové) proměnné):[16]
- axiom definice množiny:
- axiom existence množiny:
- axiom extenzionality pro třídy:
- schéma existence tříd: kde je libovolná formule jazyka teorie množin
- axiom dvojice:
- axiom nahrazení:
New Foundations[editovat | editovat zdroj]
New Foundations (NF) je axiomatizace, kterou vyvinul Willard van Orman Quine. Jedná se o zjednodušení teorie typů z knihy Principia Mathematica. Na rozdíl od teorie typů nepoužívá hierarchii typů. Axiomy NF vylučují axiom výběru.[17]
Je založena na těchto axiomech:[18]
- axiom extenzionality: Dva objekty jsou stejné, pokud se skládají ze stejných prvků.
- schéma axiomů vydělení: Množina existuje, když je formule logiky prvního řádu, která může být odvozena z dobře definované formule teorie typů odstraněním všech indexů typů (za zajištění toho, že proměnné různých typů nesplynou).
Schéma axiomů vydělení, může být nahrazeno konečně mnoha svými případy. Použití konečné axiomatizace odstraňuje nutnost v definicích zmiňovat typy.[18][19]
Často se používá ve schématu vydělení koncept vrstvené formule (anglicky stratified formula). (Řekneme, formule je vrstvená, jestliže existuje funkce) f taková, že všem objektům univerza vrátí přirozené číslo a pro platí a pro platí . Schéma axiomů vydělení pak zní:
- existuje pro každou vrstvenou formuli .[20]
Teorie polomnožin[editovat | editovat zdroj]
Teorie polomnožin byla vyvinuta v 70. a 80. letech 20. století Petrem Vopěnkou a Petrem Hájkem[zdroj?]. Její axiomatizace je podobná Von Neumannově-Gödelově-Bernaysově teorii množin, ale liší se tím, že umožňuje existenci vlastních tříd, které jsou částí nějaké množiny (). Tato vlastnost umožňuje polomnožinám sloužit jako základ Vopěnkovy alternativní teorie množin[21]
Axiomatizace konečných množin[editovat | editovat zdroj]
K některým axiomatizacím teorie množin lze nadefinovat i odpovídající axiomatizace konečných množin.
Například ZFFin získáme ze ZF tak, že axiom nekonečna nahradíme jeho negací.[22] Obdobně se získají NBGFin (respektive KMFin).
Dá se dokázat, že:
- všechny uvedené teorie jsou bezesporné.[pozn 5]
- KMFin je ostře silnější než ZFFin.
Odkazy[editovat | editovat zdroj]
Poznámky[editovat | editovat zdroj]
- ↑ Stačí si uvědomit, že s každým přidaným (z ostatních axiomů neodvoditelným) axiomem se rozšiřuje množina dokazatelných tvrzení, a navíc se může stát, že naše teorie se stane spornou (tedy se dá dokázat nějaké tvrzení i jeho negace).
- ↑ Gödelovy věty o neúplnosti vyžadují rekurzivně spočetný jazyk, což je slabší podmínka, než rekurzivní jazyk. Teorie používané v praxi ovšem splňují mnohem přísnější podmínky, než existence obecného (neomezeně složitého) algoritmu; viz například schéma nahrazení nebo schéma indukce – jsou definovány jednoduchými operacemi s řetězci. Do tohoto schématu patří každý řetězec znaků. který vznikne dosazením libovolné formule do předem daného řetězce.
Příkladem teorie, která není rekurzívně spočetná (tj. nesplňuje ani nejslabší z výše uvedených podmínek) je teorie v jazyce Peanovy aritmetiky (PA), která obsahuje jako axiomy všechny formule, které jsou pravdivé ve struktuře přirozených čísel (tato struktura je jen jeden z mnoha možných modelů PA). Je tedy rozšířením PA, ovšem na rozdíl od ní umí dokázat, že PA je bezesporná. Tato teorie by byla pro mnoho praktických účelů užitečnější, než PA, ale je v praxi nepoužitelná, neboť neexistuje způsob, jak ověřit, zda nějaké tvrzení je nebo není jejím axiomem. - ↑ To platí proto, že teorie, jejíž bezespornost zkoumáme, je zároveň teorií, které věříme, že popisuje platné matematické pravdy. Pokud zkoumáme nějakou slabší teorii, například PA, pak na důkaz její bezespornosti sice nestačí PA, ovšem stačí na ni naše „znalost matematiky“ (která je reprezentována například teorií ZFC); v té lze ukázat, že přirozená čísla tvoří model PA a z toho odvodit její bezespornost).
- ↑ Mezi axiomy ZF se někdy uvádějí i axiom existence množiny a schéma axiomů vydělení (Je-li formule, která neobsahuje volnou proměnnou z, potom formule ) je axiomem teorie. Tyto axiomy však lze odvodit z ostatních axiomů. Jmenovitě axiom existence množiny plyne okamžitě z axiomu nekonečna a schéma axiomů vydělení ze schématu axiomů nahrazení.[8][9] Tyto axiomy jsou však potřebné pro dílčí axiomatizace (Zermelova teorie množin a Fraenkelova teorie množin).[7]
- ↑ Stačí si uvědomit, že konečné teorie jsou slabší než odpovídající teorie s nekonečny.
Reference[editovat | editovat zdroj]
- ↑ Jiří Velebil, Naivní teorie množin, 27. února 2008: 15/16.Chybí název periodika! [cit. 2011-05-17]. Dostupné v archivu pořízeném z originálu dne 2020-05-30.
- ↑ Zermelo, Ernst: Untersuchungen über die Grundlagen der Mengenlehre, Mathem. Annalen 1908[nedostupný zdroj]
- ↑ Encyclopedia of Mathematics [online]. Springer [cit. 2019-02-15]. Kapitola Axiom of choice. Dostupné online.
- ↑ Encyclopedia of Mathematics [online]. Springer [cit. 2019-02-15]. Kapitola Continuum hypothesis. Dostupné online.
- ↑ Encyclopedia of Mathematics [online]. Springer [cit. 2019-02-15]. Kapitola Gödel constructive set. Dostupné online.
- ↑ Encyclopedia of Mathematics [online]. Springer [cit. 2019-02-15]. Kapitola Suslin hypothesis. Dostupné online.
- ↑ a b BALCAR, Bohuslav; ŠTĚPÁNEK, Petr. Teorie množin. 2. vyd. Praha: Academia, 2001. 464 s. Dostupné online. ISBN 80-200-0470-X. Kapitola I2, s. 35-43.
- ↑ BALCAR, Bohuslav; ŠTĚPÁNEK, Petr. Teorie množin. 2. vyd. Praha: Academia, 2001. 464 s. Dostupné online. ISBN 80-200-0470-X. Odstavec I2.27, s. 35-43.
- ↑ Metamath Proof Explorer, Theorem axsep.
- ↑ BALCAR, Bohuslav; ŠTĚPÁNEK, Petr. Teorie množin. 2. vyd. Praha: Academia, 2001. 464 s. Dostupné online. ISBN 80-200-0470-X. Odstavec I7, s. 102.
- ↑ a b c SZUDZIK, Matthew. "von Neumann-Bernays-Gödel Set Theory." From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein [online]. Wolfram [cit. 2010-10-08]. Dostupné online. (anglicky)
- ↑ SOCHOR, Antonín. Metamatematika teorií množin. Praha: Karolinum, 2005. 205 s. ISBN 80-246-1160-0. Kapitola Paragraf 4, s. 55.
- ↑ SOCHOR, Antonín. Metamatematika teorií množin. Praha: Karolinum, 2005. 205 s. ISBN 80-246-1160-0. S. 19.
- ↑ COHEN, Paul J. Set Theory and the Continuum Hypothesis. New York: Benjamin, 1966. 160 s. Dostupné online.
- ↑ SOCHOR, Antonín. Metamatematika teorií množin. Praha: Karolinum, 2005. 205 s. ISBN 80-246-1160-0. Kapitola Paragraf 2, s. 47.
- ↑ R.B. Chuaqui, Axiomatic set theory
- ↑ New Foundations home page - Big problem. math.boisestate.edu [online]. [cit. 2011-05-17]. Dostupné v archivu pořízeném z originálu dne 2020-03-21.
- ↑ a b New Foundations home page - Definition. math.boisestate.edu [online]. [cit. 2011-05-17]. Dostupné v archivu pořízeném z originálu dne 2020-03-21.
- ↑ Hailperin, T. “A set of axioms for logic,” Journal of Symbolic Logic 9, pp. 1-19.
- ↑ Forster, Thomas, "Quine's New Foundations", The Stanford Encyclopedia of Philosophy (Summer 2009 Edition), Edward N. Zalta (ed.)
- ↑ http://eom.springer.de/A/a110560.htm Springer, Encyclopaedia of Mathematics: Petr Vopěnka - Alternative set theory
- ↑ SOCHOR, Antonín. Metamatematika teorií množin. Praha: Karolinum, 2005. 205 s. ISBN 80-246-1160-0. S. 17.

























































