Lineární zobrazení
Pojmem lineární zobrazení (někdy též lineární transformace, angl. linear map, linear mapping, popř. linear transformation) se v matematice označuje takové zobrazení mezi vektorovými prostory X a Y, které zachovává vektorové operace sčítání a násobení skalárem. Název lineární je odvozen z faktu, že grafem lineárního zobrazení z reálných čísel do reálných čísel je přímka, latinsky linea.
Důležitými zástupci lineárních operací jsou například derivování a integrování funkcí. Pomocí lineárních zobrazení lze popisovat i rotace a jednoduché deformace objektů ve vektorových prostorech. Oblast, kde lineární zobrazení nacházejí uplatnění je kvantová mechanika, kde je každý vývoj systému a každé měření popsáno právě pomocí lineárních zobrazení. Kvantová mechanika je sama o sobě natolik významná teorie, že studovat vlastnosti lineárních zobrazení je důležité už pro ni samotnou. Lineární zobrazení obecně zaujímají v matematice a ve fyzice velmi důležité postavení. Jedním z hlavních důvodů je relativní snadnost manipulace s takovýmito zobrazeními. Máme-li nějaké nelineární zobrazení, s nímž se pro jeho příliš složitou strukturu obtížně pracuje, můžeme si v některých případech vypomoci jeho jednodušší linearizovanou variantou. Tento postup se používá ve fyzice, kde rovnice popisující fyzikální děj často nabývají tvaru, který je těžko řešitelný. Po zjednodušení takové rovnice lze problém vyřešit. Ovšem za cenu toho, že dané řešení nepopisuje probíhající fyzikální děj zcela přesně. Podobná metoda nahrazování složitých funkcí jejich lineárními protějšky je používána i v matematice, kde je důvodem opět snazší nakládání s výslednými matematickými výrazy.
Motivace
[editovat | editovat zdroj]
Než přikročíme k definici je vhodné si uvést příklad jednoduchých funkcí, abstrakcí jejichž vlastností dospějeme právě k obecné definici lineárního zobrazení. Mezi nejjednodušší funkce, které si lze představit, jsou funkce tvaru
kde a a b jsou parametry. Jedná se tedy o funkce na reálných číslech tvaru výše s reálnými parametry a a b, konkrétně např. či . Když se tyto funkce vyjádří graficky, je vidět, že jejich grafem je přímka, viz obrázek. Neboť latinské slovo pro přímku zní linea (další významy zahrnují i "čára", "provázek" či "lněná nit"), označují se funkce tohoto tvaru jako lineární. Pokud je parametr b roven nule, tak tato přímka prochází počátkem souřadnic, viz funkci g na obrázku.
Prostudujme nyní v krátkosti základní vlastnosti lineárních funkcí. Uvažujme přitom jen takové lineární funkce, které mají parametr , tj. jsou tvaru . Pokud necháme takovéto funkce působit na součet a na násobek , tak obdržíme
Z řádku výše tedy vidíme obecnou vlastnost funkcí s :
- .
Jedná se o dvě vlastnosti, první se nazývá aditivita, druhá pak homogenita. První říká, že je jedno, zda nejdříve čísla sečteme a pak na ně aplikujeme funkci, nebo naopak. Druhá vlastnost tvrdí totéž o násobení číslem. Pro matematika to znamená, že úprava matematických vzorců s těmito funkcemi bude z uvedených důvodů velmi snadná. Právě tyto dvě vlastnosti slouží k definici obecného lineární zobrazení tak, jak je podána v následujícím oddíle. Zobrazení splňujících tyto vlastnosti je překvapivě velké množství, viz oddíl Příklady níže.
Uveďme si ještě dvě další zajímavé vlastnosti lineárních funkcí. Když sečteme funkce f a g tvaru a , dostaneme funkci téhož tvaru:
- ,
kde v roli parametrů nyní vystupují čísla a . Když funkci f vynásobíme číslem , obdržíme funkci , jež je opět lineární, neboť
Vidíme tedy, že součtem dvou lineárních funkcí či jejich vynásobením číslem dostaneme opět lineární funkci. Matematicky řečeno je množina lineárních funkcí uzavřená na součet a násobení číslem. Zdůrazněme, že v předchozím odstavci jsme zjišťovali chování jednotlivých funkcí tvaru . O každé takové funkci jsme věděli, že splňuje dvě vlastnosti, aditivitu a homogenitu. Tyto vlastnosti se týkají součtu a násobení argumentu funkce, čísla. V tomto odstavci jsme naproti tomu zjišťovali, co dostaneme součtem či vynásobením dvou takových funkcí.
Definice
[editovat | editovat zdroj]Lineární zobrazení
[editovat | editovat zdroj]Nechť X a Y jsou vektorové prostory nad týmž tělesem . Zobrazení z prostoru X do prostoru Y, tj. , se nazývá lineární zobrazení, právě když pro libovolné vektory a pro libovolný prvek z tělesa toto zobrazení splňuje následující dvě podmínky:
- aditivita: ,
- homogenita: .
Obraz vektoru při lineárním zobrazení se značí . Často se ale pro jednoduchost závorky vypouští a píše se jen . Podobně obraz množiny se značí .
Lineární struktura zobrazení i vektorového prostoru, na kterém je definováno, umožňuje velmi zjednodušit zápis, jakým toto zobrazení působí na libovolný vektor. Tato vlastnost tím spíše vyplyne na konečně rozměrných prostorech. Mějme vektorový prostor konečné dimenze n. Existuje v něm tedy n-členná báze a každý vektor tohoto prostoru lze vyjádřit jako vhodnou lineární kombinaci . Využijeme-li nyní linearity zobrazení A, dostáváme
Obraz každého vektoru lze tedy vyjádřit jako nějakou lineární kombinaci vektorů , kde koeficienty jsou totožné s koeficienty u vzoru . Celou informaci o struktuře zobrazení A lze tak získat pouze ze znalosti toho, jak působí na bazické vektory. Rozvinutím právě uvedené myšlenky pak dospíváme k definici matice lineárního zobrazení, jak je uvedeno níže.
Příbuzné pojmy
[editovat | editovat zdroj]Lineární zobrazení se nazývá lineární operátor, právě když ve výše uvedené definici je prostor Y totožný s prostorem X. Neboli zobrazení L je lineární operátor, právě když je lineární podle definice výše a platí . Často se ale pojem zobrazení a operátor zaměňuje a lze se setkat i s lineárními zobrazeními, pro něž a která jsou přitom i přesto označována jako operátory.
Dalším zajímavým typem lineárního zobrazení je lineární funkcionál. Lineární funkcionál je lineární zobrazení z prostoru X do tělesa , nad nímž je prostor X definován. Každému vektoru z X tak přiřazuje skalár z .
Při klasifikaci různých druhů lineárních zobrazení, resp. operátorů, se používá následující názvosloví. Řekneme, že lineární zobrazení , které zobrazuje prostor X do prostoru Y je
- monomorfní, právě když je prosté,
- epimorfní, právě když je na,
- izomorfní, právě když je prosté a na, tj. je to bijekce,
- regulární operátor, právě když je prosté a je to lineární operátor, tj. X = Y.
Antilineární zobrazení
[editovat | editovat zdroj]Jako dvojník lineárnímu zobrazení se definuje i antilineární zobrazení, které se od lineárního liší pouze v tom, že při vytýkání skaláru tento komplexně sdružíme. Přesně tedy nechť X a Y jsou vektorové prostory nad týmž číselným tělesem . Zobrazení z prostoru X do prostoru Y, tj. , se nazývá antilineární zobrazení, právě když pro libovolné vektory a pro libovolné číslo z tělesa toto zobrazení splňuje následující dvě podmínky:
- aditivita:
- antihomogenita:
kde značí komplexní sdružení čísla .
Multilineární, bilineární, seskvilineární zobrazení
[editovat | editovat zdroj]Pojem linearity lze zobecnit i na zobrazení více proměnných. Mějme zobrazení L z konečného kartézského součinu vektorových prostorů do jistého vektorového prostoru, tj. . Pak nazýváme multilineární zobrazení právě, když je lineární v každé své proměnné. Neboli, mějme libovolné vektory a skaláry , kde je těleso společné všem vektorovým prostorům . Pak L je multilineární právě, když
- aditivita:
- homogenita:
Mezi multilineární zobrazení patří například tenzory, k-formy či diferenciální formy. Velmi často se lze setkat s multilineárními zobrazeními dvou proměnných, tj. v definici výše. Taková zobrazení se nazývají bilineární. Zobrazení je tedy bilineární právě, když
Podobné zobrazení k bilineárnímu je seskvilineární zobrazení (latinská předpona sesqui- znamená "jeden a půl(krát)"). Přísně vzato zde již vybočujeme z lineárních zobrazení, protože seskvilineární zobrazení je zobrazení dvou proměnných, přičemž v jedné z nich je lineární a ve druhé je antilineární. Velmi důležitým příkladem seskvilineárního zobrazení je skalární součin. Matematici a fyzikové přitom nejsou zajedno, ve které proměnné je zobrazení antilineární a uplatňují se tak dvě různé konvence. Zde uvedeme definici, v níž je zobrazení antilineární ve druhé proměnné. Zobrazení je seskvilineární právě, když
kde značí komplexní sdružení čísla (za bereme číselné těleso). Jediný rozdíl oproti bilineárnímu zobrazení je tedy ten, že vytknutí čísla z druhé proměnné způsobí, že se toto číslo komplexně sdruží.
Prostory lineárních zobrazení
[editovat | editovat zdroj]Množina všech lineárních zobrazení z prostoru X do prostoru Y se obvykle označuje symbolem , podobně množina všech lineárních operátorů na prostoru X se značí . Tyto množiny jsou uzavřené na sčítání dvou zobrazení a na jejich násobení skalárem, definujeme-li obě operace následujícím způsobem:
Součet zobrazení je zobrazení , které pro každý vektor splňuje
- .
Násobek zobrazení prvkem je zobrazení , které pro každý vektor splňuje
- .
Uzavřenost je snadno nahlédnutelná v případě lineárních funkcí tak, jak je to ukázáno v druhé části oddílu Motivace výše. Lze dokonce ukázat, že samotná
- množina lineárních zobrazení je vektorový prostor.
Nastiňme nyní důkaz. Pro existenci vektorového prostoru potřebujeme čtyři věci. Neprázdnou množinu , těleso , operaci sčítání vektorů a operaci násobení vektoru prvkem z tělesa, skalárem. Jako vektory nyní vystupují samotná lineární zobrazení, sčítání a násobení jsme si výše právě definovali. V definici lineárního zobrazení z prostoru X do prostoru Y jsme požadovali, aby tyto prostory byly nad stejným tělesem . Toto těleso použijeme i jako těleso pro náš právě budovaný vektorový prostor lineárních zobrazení. Konečně jako množinu vezmeme množinu , která je jistě neprázdná. Pro libovolné vektorové prostory X a Y zde totiž jistě leží nulové lineární zobrazení, které každému vektoru z X přiřazuje nulový vektor z Y. Je množina uzavřená na sčítání a násobení lineárních zobrazení? Neboli, je součet či násobek lineárních zobrazení opět lineární zobrazení? Pro libovolná platí
kde jsme v první rovnosti využili definici sčítání zobrazení a jejich linearitu. Ve druhé rovnosti jsme pak přeskupili členy coby vektory v Y a tyto přeskupené členy jsme opět dali dohromady využívajíce definice součtu zobrazení. Máme tak ověřenu aditivitu zobrazení A+B. Podobně ověříme i homogenitu:
Nyní víme, že součet lineárních zobrazení je opět lineární zobrazení. Analogicky bychom ověřili, že násobek lineárního zobrazení je lineární zobrazení.
Zbývá nám tedy ještě dokázat axiomy vektorového prostoru, abychom mohli shrnout, že je vektorový prostor:
- komutativita sčítání lineárních zobrazení: , kde první a poslední rovnost plyne z definice sčítání zobrazení a druhá rovnost plyne z toho, že vektory v prostoru Y komutují,
- asociativita sčítání lineárních zobrazení: ověřila by se naprosto analogicky jako komutativita,
- nulovým prvkem je nulové lineární zobrazení zmíněné výše,
- opačným vektorem k zobrazení A je zjevně (-1) A, kde -1 je prvek tělesa opačný k jednotkovému prvku,
- ostatní vlastnosti zmíněné v definici vektorového prostoru by se ověřili analogicky prvnímu bodu s komutativitou.
Související pojmy
[editovat | editovat zdroj]Jádro zobrazení
[editovat | editovat zdroj]Jádro lineárního zobrazení A je taková podmnožina definičního oboru A, kterou A zobrazuje na nulový vektor. Jádro zobrazení A značíme symbolem (jedná se o zkratku ze slova kernel, anglického označení pro jádro). Přesněji: Mějme dva vektorové prostory X a Y nad stejným tělesem . Dále nechť A je lineární zobrazení z X do Y, tj.. Pak jádro zobrazení A je množina
kde označuje nulový vektor v prostoru Y. Dimenze jádra zobrazení A, tj. , se občas označuje jako defekt zobrazení A. Z vlastností v oddíle Nulový vektor je vidět, že nulový vektor leží v jádře každého lineárního zobrazení. Dokonce lze dokázat následující tvrzení: Lineární zobrazení je prosté právě tehdy, když v jeho jádru leží pouze nulový vektor (důkaz viz Prostota zobrazení). Neboť množina je také vektorový (pod)prostor, tak lze využít tvrzení z oddílu Obrazy a vzory vektorů a jejich podprostorů o vzoru podprostoru abychom uviděli, že jádro zobrazení je vektorový podprostor, tj.
Hodnost zobrazení
[editovat | editovat zdroj]Jako hodnost zobrazení A, ozn. h(A), se občas označuje dimenze oboru hodnot lineárního zobrazení A, tj. . Platí, že hodnost zobrazení splňuje nerovnosti:
- Důkaz: Druhá nerovnost plyne přímo z toho, že obor hodnot A(X) je podprostorem prostoru Y. První nerovnost zjevně platí pro případy nebo . Pro konečnou nenulovou dimenzi vezměme bázi prostoru X, kterou si označme . Pak obraz prostoru X při zobrazení A je lineární obal a tedy .
Matice zobrazení
[editovat | editovat zdroj]Linearita nějakého zobrazení je natolik omezující vlastnost, že pro charakterizaci takovéhoto zobrazení stačí uvést jeho hodnoty jen v (relativně) malém počtu bodů. Tato vlastnost tím více vyplyne na konečněrozměrných vektorových prostorech. Pro konkrétnost tedy mějme lineární zobrazení , kde oba vektorové prostory jsou konečných dimenzí, . V obou prostorech tedy existuje jejich báze, označme bazické vektory prostoru X jako a podobně nechť je báze prostoru Y. Libovolný vektor z prostoru X lze tedy zapsat jako lineární kombinaci bazických vektorů
Pak působením zobrazení A na takovýto vektor dostáváme vektor , pro nějž platí
Dále, vektory leží v prostoru Y, takže je lze vyjádřit jako lineární kombinace bazických vektorů ve tvaru
Například pro vektor tak máme , pro vektor máme , pro vektor máme atd. Celkově tedy
Rozeberme nyní právě obdržený výraz. Koeficienty v tomto výrazu pocházejí z lineární kombinace pro vstupní vektor a vektory jsou předem zadaná báze prostoru Y. Jediné, co tedy charakterizuje zobrazení A samotné jsou tak prvky . Tyto si můžeme uspořádat do matice tvaru
Této matici se říká matice zobrazení A v bázích a , kde jsme označili bázi prostoru X jako a bázi prostoru Y jako . Tato matice plně popisuje strukturu lineárního zobrazení A. Značí se symbolem
- .
Konkrétní tvar matice zobrazení záleží na bázích jednotlivých prostorů, v nichž je vyjádřena. Pro jedno lineární zobrazení tak máme více matic zobrazení, neboť báze prostorů nejsou určeny jednoznačně a my si je můžeme volit různými způsoby. Vždy je tedy nutno uvést, v jakých bázích je daná matice zobrazení vyjádřena. Naproti tomu, všechny takové matice zobrazení jsou svázány převodními pravidly. Tato pravidla jsou shrnuta v matici přechodu. Mějme matici zobrazení A v bázích a , jež označíme . Mějme dále matici téhož zobrazení v bázích a , kterou si označíme jako . Tyto dvě matice jsou pak v následujícím vztahu:
kde je matice přechodu od báze k bázi a podobně je matice přechodu od báze k bázi a symbol značí maticové násobení.
Matice zobrazení tak představuje přechod od lineárních operátorů k maticím. Skládání lineárních zobrazení se tak redukuje na násobení matic, podobně působení lineárního zobrazení na vektor je nyní představováno násobením vektoru maticí. Práce se zobrazeními se tak zjednodušuje.
Spektrum zobrazení, vlastní čísla
[editovat | editovat zdroj]V mnoha případech je vhodné zjišťovat, zda v daném vektorovém prostoru neexistuje vektor, na nějž působí dané lineární zobrazení zvlášť jednoduchým způsobem. Takové vektory určují množinu prvků z tělesa, skalárů, které jsou jistým způsobem význačné. Této množině se říká spektrum lineárního operátoru. Spektrum je definováno pro lineární zobrazení jak na konečněrozměrných, tak i nekonečněrozměrných, prostorech. Na těch konečněrozměrných pak spektrum nabývá zvlášť jednoduché podoby, kterou si nyní představíme. Mějme lineární zobrazení vektorového prostoru X do vektorového prostoru Y. Nechť jsou tyto prostory definovány nad číselným tělesem . Pak každé číslo , pro něž existuje nějaký nenulový vektor tak, že
nazveme vlastní číslo zobrazení A a patřičný vektor nazveme vlastní vektor zobrazení A příslušný vlastnímu číslu . Množině všech vlastních čísel daného lineárního zobrazení říkáme spektrum. Vlastní vektory jsou tedy takové vektory, na které působí zobrazení A jen jako násobení nějakým číslem. Tomuto číslu pak říkáme vlastní číslo.
S vlastními vektory a vlastními čísly se úzce pojí pojem diagonalizovatelnosti lineárních operátorů. Zhruba řečeno, existuje-li v daném vektorovém prostoru báze z vlastních vektorů daného lineárního operátoru, pak je matice tohoto operátoru v takové bázi diagonální.
Lineární zobrazení vs. skalární součin
[editovat | editovat zdroj]Pokud jsou vektorové prostory, mezi kterýmiž lineární zobrazení zobrazuje, vybaveny skalárním součinem, lze studovat vlastnosti takovéhoto lineárního zobrazení do větší hloubky. Můžeme totiž nyní navíc zjišťovat, jak se dané zobrazení chová ve vztahu ke skalárnímu součinu. Následující pojmy lze zavést opět pro lineární zobrazení působící jak na nekonečněrozměrných, tak i konečněrozměrných prostorech. Pro jednoduchost budeme uvažovat jen prostory konečněrozměrné. Nekonečněrozměrné případy lze nalézt pod jednotlivými hesly pro konkrétní druhy zobrazení.
Pro jednoduchost budeme tedy uvažovat lineární zobrazení na konečněrozměrném prostoru , kde navíc , tj. A je lineární operátor na X. Nechť je vektorový prostor X, definovaný nad číselným tělesem , vybaven skalárním součinem . Z Rieszovy věty lze dokázat, že pro takový operátor A existuje právě jeden lineární operátor B splňující pro každou dvojici vektorů vztah
Operátoru B se říká operátor sdružený k operátoru A a značí se , popř. . Jedná se o tak důležitý pojem, že se zavádí následující názvosloví. Lineární operátor A se nazývá:
- Normální operátor, právě když komutuje se svým sdružením, tj.
- Samosdružený operátor, právě když je roven svému sdružení, tj.
V této souvislosti se ještě rozlišují další pojmy podle toho, zda je těleso reálné či komplexní. Operátor A se nazývá
- Symetrický operátor právě, když je A samosdružený a těleso je tvořeno reálnými čísly, tj.
- Hermitovský operátor právě, když je A samosdružený a těleso je tvořeno komplexními čísly, tj.
- Izometrický operátor právě, když je jeho sdružení rovno jeho inverzi, tj.
kde I značí identické zobrazení. Podobně jako u samosdružených operátorů se dále operátor A nazývá
- Ortogonální operátor právě, když je A izometrický a těleso je tvořeno reálnými čísly, tj.
- Unitární operátor právě, když je A izometrický a těleso je tvořeno komplexními čísly, tj.
Obecné vlastnosti
[editovat | editovat zdroj]V následujícím uvažujeme lineární zobrazení nějakého vektorového prostoru X do nějakého obecně jiného vektorového prostoru Y. Předpokládáme tedy, že lineární zobrazení je definované na celém prostoru, ze kterého zobrazuje.
Aritmetické operace
[editovat | editovat zdroj]Pro lineární zobrazení A, B a C s patřičnými definičními obory platí následující zjevné vztahy:
- tj. skládání zleva je distributivní,
- tj. skládání zprava je distributivní,
- tj. násobení skalárem je asociativní,
- tj. skládání je asociativní,
- obecně , tj. skládání není obecně komutativní.
Nulový vektor
[editovat | editovat zdroj]- Obraz nulového vektoru při libovolném lineárním zobrazení je opět nulový vektor, neboli
kde označuje nulový vektor v prostoru X, zatímco označuje nulový vektor v prostoru Y.
- Důkaz: , kde vektor je volen libovolně.
Podmínky linearity
[editovat | editovat zdroj]- Nechť A je nějaké zobrazení z vektorového prostoru X do vektorového prostoru Y, pak následující tři tvrzení jsou ekvivalentní:
- , tj. A je lineární,
- , tj. není třeba ověřovat aditivitu a homogenitu zvlášť, ale stačí je ověřovat dohromady,
- .
- Důkaz: Implikace z 1 do 2 plyne ihned. Implikace z 3 do 1 plyne taky ihned, stačí položit n=2 a pro ověření aditivity a n=1 pro důkaz homogenity. Pokud nyní dokážeme implikaci z 2 do 3, uzavřeme tak kruh implikací a věta bude dokázána. Dokažme matematickou indukcí nyní tedy implikaci z 2 do 3. Z tvrzení výše o nulových vektorech již víme , což jsme dokázali způsobem, který je kompatibilní s bodem 2, ze kterého nyní vycházíme. Jako počáteční krok indukce uvažme n=1. Pak . Pro indukční krok nyní předpokládáme platnost pro n a dokazujeme platnost pro n+1, označme si libovolnou lineární kombinaci n vektorů jako , pak z bodu 2 plyne . Z indukčního předpokladu lze napsat ve chtěném tvaru a důkaz je tedy dokončen.
Zúžení zobrazení
[editovat | editovat zdroj]- Zúžení lineárního zobrazení na podprostor je opět lineární zobrazení, tj.
kde značí zúžení zobrazení A na podprostor P.
- Důkaz: Podprostor je uzavřen na sčítání vektorů a jejich násobení skalárem. Můžeme tak použít postupu podobného tomu výše k ověření homogenity a aditivity zobrazení A na vektorech ležících jen v daném podprostoru P.
Inverzní a složené zobrazení
[editovat | editovat zdroj]- Inverze k lineárnímu zobrazení je opět lineární zobrazení. Přesněji, nechť je izomorfní zobrazení (tj. lineární bijekce definovaná na celém X), pak existuje inverzní zobrazení , které je též izomorfní.
- Důkaz: Neboť je z předpokladů A bijekce, tak určitě existuje její inverze , zbývá ověřit její linearitu. Označme si , , kde vektory jsme si vybrali libovolně. Z linearity zobrazení A plyne . Zobrazení A tedy vektoru přiřadilo vektor . Jeho inverze tedy učiní opak dostávajíc . Když si rozepíšeme, jak vznikly vektory a dospíváme k výrazu , což je ekvivalentní s linearitou zobrazení .
- Složené zobrazení z lineárních zobrazení je opět lineární. Přesněji, nechť a . Pak složené zobrazení BA definované vztahem
pro všechna je lineární, tj. .
- Důkaz: Vezměme libovolné a libovolné vektory . Pak , což je ekvivalentní linearitě složeného zobrazení.
Obrazy a vzory vektorů a jejich podprostorů
[editovat | editovat zdroj]- Obraz, resp. vzor, podprostoru podle lineárního zobrazení je opět podprostor. V symbolech
kde označuje vzor množiny Q při zobrazení A.
- Důkaz: Uvažujme nejprve obraz podprostoru P při zobrazení A. O tomto zobrazení předpokládejme, že P leží v jeho definičním oboru. Množina A(P), tj. obraz podprostoru P, je podmnožinou prostoru Y. Chceme ukázat, že pro libovolné dva vektory a libovolné platí, že kombinace leží opět v množině A(P). Pro vektory máme určitě nějaké vektory tak, že a . Úpravou tak zjišťujeme, že je tento výraz roven obrazu vektoru . Neboli, našli jsme vektor, konkrétně , ležící v P, jehož obrazem je právě naše původní kombinace a tato kombinace tak skutečně patří do A(P). Obdobně pro vzor podprostoru Q při zobrazení A. Označme si tento vzor jako . Máme-li a nějaké , tak chceme ukázat, že i kombinace leží v množině . Z předpokladů existují nějaké vektory tak, že a . Z linearity zobrazení A ale opět . Neboť je Q vektorový podprostor, tak kombinace leží v tomto podprostoru. Vektor je tak vzorem nějakého vektoru z Q a patří tedy do , což jsme chtěli dokázat.
Následuje čtveřice podobných tvrzení vztahujících se k lineární nezávislosti vzoru a obrazu množiny vektorů:
- Obraz lineárně závislé množiny vektorů podle lineárního zobrazení je opět lineárně závislá množina.
- Vzor lineárně závislé množiny vektorů podle monomorfního zobrazení je opět lineárně závislá množina.
- Vzor lineárně nezávislé množiny vektorů podle lineárního zobrazení je opět lineárně nezávislá množina.
- Obraz lineárně nezávislé množiny vektorů podle monomorfního zobrazení je opět lineárně nezávislá množina.
- Důkaz: Důkaz prvního tvrzení: Mějme lineárně závislou (konečnou) množinu vektorů , tj. existují koeficienty tak, že a přitom existuje koeficient, který je nenulový. Neboť obraz nulového vektoru je opět nulový vektor, tak když na obě strany rovnosti zapůsobíme zobrazením A, dostaneme . Neboť se koeficienty nezměnili, tak soubor vektorů je opět lineárně závislý. Důkaz druhého tvrzení: Nechť jsou vzory lineárně závislých vektorů , tj. . Existuje tedy lineární kombinace , kde je alespoň jeden koeficient nenulový. Jenže . Obraz vektoru v závorkách je tedy nulový vektor. Vektor v závorkách tedy leží v jádře zobrazení A. Protože se bavíme o monomorfním, tzn. prostém, zobrazení, tak z vlastnosti v oddílu Nulový vektor plyne, že kombinace , tj. vektor ležící v jádře A, je nutně roven nulovému vektoru. Máme tedy s alespoň jedním nenulovým koeficientem. Vektory jsou tedy lineárně závislé. Důkaz třetího tvrzení – sporem: Nechť je vzor lineárně nezávislé množiny lineárně závislá množina. Pak z prvního tvrzení plyne, že obraz této množiny je lineárně závislá, což je spor. Důkaz čtvrtého tvrzení – sporem: Nechť je monomorfní obraz lineárně nezávislé množiny množina lineárně závislá. Pak z druhého tvrzení plyne, že vzor této množiny je lineárně závislý, což je spor.
- Obraz lineárního obalu je lineární obal obrazů. Neboli
- Důkaz: Ukažme nejprve inkluzi zleva doprava. Máme tedy nějaký vektor , který je obrazem vektoru tvaru , tj. . Pak vektor lze vyjádřit jako lineární kombinaci obrazů způsobem a leží tak v lineárním obalu obrazů. Pro důkaz opačné inkluze postupujeme naprosto analogicky předchozímu postupu, kde opět využíváme linearity zobrazení A.
- Vztah pro vzor vektoru při lineárním zobrazení: Nechť je lineární zobrazení a je vektor z jeho oboru hodnot. Dále nechť vektor leží ve vzoru vektoru (pokud A není prosté, tak ve vzoru leží více vektorů), tj. . Pak pro vzor platí
kde značí jádro zobrazení A.
- Důkaz: Dokažme nejprve inkluzi zprava doleva. Mějme libovolný vektor z jádra, pak . Vektor tak leží ve vzoru a inkluze je dokázána. Pro důkaz opačné inkluze mějme vektor ze vzoru, platí tedy . Současně a vektor tedy leží v jádře, neboť . Libovolný vektor ze vzoru tak lze zapsat jako součet vektoru a vektoru , kde leží v jádře. Druhá inkluze je tak dokázána.
Prostota zobrazení
[editovat | editovat zdroj]- Lineární zobrazení je prosté tehdy a jen tehdy, leží-li v jeho jádru pouze nulový vektor. V matematické notaci tedy
- Důkaz: Dokažme nejprve implikaci zleva, tj. mějme prosté lineární zobrazení. Neboli pro každé dva vektory platí . Přepsáním předchozího tvrzení s využitím linearity A tedy: . Když si označíme , tak tedy . Neboli, když nějaký vektor leží v jádru, tak už je nulový. Dokažme nyní opačnou implikaci, tedy nechť v jádru leží jen nulový vektor. Uvažme pak dva vektory takové, že , tj. . Vektor tedy leží v jádru A. Z předpokladů je ale takový vektor nutně nulový tj. . Celkově tedy máme , což jsme chtěli dokázat.
- Lineární zobrazení konečněrozměrných prostorů stejné dimenze je bijekcí právě, když je prosté nebo když je na. Neboli, máme-li zobrazení , tak abychom ověřili jeho bijektivnost stačí, abychom ověřili buď jen to, že je prosté, anebo jen to, že je na. V notaci
- Důkaz: Implikace zleva doprava vyplývá přímo z definice. Zaměřme se tedy na opačnou implikaci a uvažujme nejprve lineární zobrazení A, o němž víme pouze to, že je prosté. Mějme dále bázi prostoru X, kterou si označíme . Pak množina obrazů je z vlastnosti v oddíle Obrazy a vzory vektorů a jejich podprostorů lineárně nezávislá. Jedná se o n-prvkovou podmnožinu lineárně nezávislých vektorů v n-rozměrném prostoru Y, je to tedy báze v Y. Z linearity zobrazení A dokážu každý vektor vyjádřit v bázi jako . K vektoru jsem tak našli jeho vzor z prostoru X a tedy . Protože jsme volili libovolně, můžeme shrnout, že . Uvažujme nyní zobrazení A, o němž víme jistě jen to, že je na, tj. pro každý vektor existuje tak, že Takže i pro bazické vektory prostoru Y najdeme takové vektory , že . Protože z vlastností v oddíle Obrazy a vzory vektorů a jejich podprostorů plyne, že vzor lineárně nezávislých vektorů je opět lineárně nezávislý, tak vektory tvoří bázi prostoru X. Abychom dokázali, že je A prosté, musíme ukázat, že v jeho jádru leží jen nulový vektor, viz předchozí tvrzení v tomto oddíle. Kdyby v jeho jádře existoval nějaký nenulový vektor obecného tvaru , tak musí platit . Vektory jsme ale na počátku zvolili jako lineárně nezávislé. Jediná lineární kombinace dávající nulový vektor je tedy pouze ta mající všechny koeficienty nulové, tj. . Neboli vektor je nutně nulový, což je spor s předpokladem.
Věta o dimenzích jádra a obrazu
[editovat | editovat zdroj]- Součet hodnosti a nulity (defektu) lineárního zobrazení je roven dimenzi definičního oboru. Neboli, mějme lineární zobrazení definované na celém X, které je konečné dimenze, tj. . Pak
kde ker A značí jádro zobrazení A a ran A označuje jeho obor hodnot.
Grafická interpretace
[editovat | editovat zdroj]
Některým třídám lineárních zobrazení se dá dát přímá grafická interpretace. Lineární zobrazení umožňuje popsat rotace, zvětšování, zmenšování, natahování, zrcadlení podle počátku či zrcadlení podle osy. Pro jednoduchost a snadnou nahlédnutelnost uvažujme vektorový prostor , který lze geometricky chápat jako rovinu. Vektory v tomto prostoru si lze představovat jako šipky v rovině, první složku šipky si označme jako x, její druhou složku pak jako y. Šipku samotnou pak označujme symbolem . Na takovémto vektorovém prostoru šipek pak definujme následující lineární operátory, jejichž maticové vyjádření ve standardní bázi zní
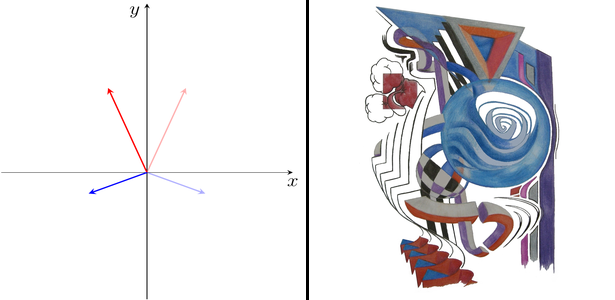
Všem těmto operátorům dáme v následujícím jejich geometrickou interpretaci. První operátor I je představován identickou maticí. Očekáváme tedy, že s vektory "nic neudělá". Skutečně,
Představme si celou věc na šipkách. Mějme tedy šipky a tak, jak je ukázáno na obrázku 1. Nechť je modrá šipka a nechť je červená šipka. Pak předchozí rovnice nevyjadřuje nic jiného, než to, že tyto dvě šipky se po působení operátoru I nezmění. Zachovají si svou velikost i směr. Abychom i pro další operátory viděli, jak působí na daném vektorovém prostoru, je účelné si jejich působení představit nejen na šipkách, ale i na výtvarných obrázcích. Pro konkrétnost zde za obrázek vezmeme malůvku vyobrazenou v pravé části obrázku 1. Každý výtvarný obrázek je složen z mnoha různě barevných bodů. Každý bod je přitom jednoznačně popsán svými dvěma souřadnicemi, x-ová souřadnice udává jeho polohu ve vodorovném směru, y-ová souřadnice pak udává jeho polohu ve svislém směru. Podobně i každá šipka alias vektor je jednoznačně popsána svými dvěma souřadnicemi. Každý bod malůvky tedy můžeme ztotožnit se šipkou, která v daném bodě končí. Pro identický operátor I tak platí, že nechává obrázek nezměněn, neboť nemění žádnou šipku, jak jsme výše viděli.
V případě ostatních operátorů je ale situace zajímavější. Šipky budou obecně měnit velikost i směr a malůvka se tak bude různě deformovat, jak vzápětí uvidíme. Na obrázcích 2 až 7 ponecháváme v jejich levé části jak původní dvě šipky, a , tak i jejich obrazy při daném zobrazení. Původní šipky jsou přitom vykresleny slabě. Pravé části obrázků 2 až 7 pak ukazují, jak se mění malůvka při působení daného zobrazení.
Co obdržíme pro operátor Z? Jeho působení na libovolný vektor zní
První složka vektoru je tedy ominusována. Graficky lze působení operátoru Z ukázat na obrázku 2. Z něho je patrné, že operátor Z představuje zrcadlení roviny podle osy y. Dále, pro operátor O dostáváme
V tomto případě tedy dochází k ominusování obou složek vektoru. Na obrázku 3 je vidět, jak se tato změna projeví graficky. Vidíme, že operátor O představuje zrcadlení roviny podle počátku souřadnic.
-
Obrázek 2: Při působení operátoru Z se pouze ominusuje x-ová složka šipky, což způsobí, že se šipka překlopí kolem osy y. To odpovídá zrcadlení podle osy y. Na malůvce je tento jev jasně zřetelný, pokud ho porovnáme s původní verzí vyobrazenou na obrázku 1.
-
Obrázek 3: Působení operátoru O ominusuje obě složky vektoru. Jak vidno z levé strany obrázku, toto odpovídá inverzi souřadnic. Všechny šipky převrátí svůj směr, ale zachovají si svou velikost. Porovnáním malůvky vpravo s tou původní vidíme, že působením operátoru O dochází ke zrcadlení podle počátku souřadnic.
Pro operátor V máme
Obě složky výsledného vektoru jsou tedy dvakrát větší, než složky vektoru původního. Graficky tato situace odpovídá dvojnásobnému zvětšení šipky, resp. obrázku, jak je možno nahlédnout na obrázku 4. Naprosto analogicky pak operátor M představuje dvojnásobné zmenšení šipky, jak lze vidět na obrázku 5. Obecně operátor tvaru
odpovídá -násobnému prodloužení, resp. zkrácení, šipky. Pokud je , pak se jedná o prodloužení, pokud , pak se jedná o zkrácení. Pokud je záporné, tak se do hry vkládá i zrcadlení podle počátku souřadnic. Pro dostáváme operátor O z obrázku 3. Pro dochází k současnému zrcadlení podle počátku a navíc prodloužení šipek. Podobně pro dochází k současnému zrcadlení podle počátku a navíc zkrácení šipek. Nakonec pro dostáváme nulové zobrazení, které každému vektoru přiřadí nulový vektor, a pro získáme identický operátor I.
-
Obrázek 4: Při zobrazení V se každá složka šipky dvakrát zvětší. Šipka si tak zachová svůj směr, ale dvakrát se prodlouží. V souhlase s tím je malůvka vpravo oproti své původní verzi dvakrát větší.
-
Obrázek 5: Zobrazení M působí podobně jako zobrazení V, pouze místo dvojnásobného zvětšení dochází k dvojnásobnému zmenšení. To můžeme opět lehce nahlédnout jak z tvaru výsledných šipek vlevo, tak z podoby malůvky napravo.
Operátor V šipky dvakrát prodlužoval, operátor M je naopak dvakrát zkracoval. Šipky lze však i v jedné složce prodlužovat a ve druhé zkracovat. To má na svědomí například operátor D, který x-ovou složku dvakrát zvětší a y-ovou složku naopak dvakrát zmenší, neboť
Na obrázku 6 vidíme, jak toto zobrazení působí. Obraz se roztáhne do šířky a navíc se ve svislém směru "zplácne".
Jako poslední příklad lineárního zobrazení jsme si uvedli operátor R, jenž na libovolný vektor působí jako
Na první pohled není zcela jasné, co toto zobrazení provádí. Nejjednodušší je rovnou pohlédnout na obrázek 7, z něhož zjistíme, že operátor R odpovídá rotaci! Jedná se o otočení vektoru kolem počátku o 45° proti směru hodinových ručiček. Operátor R je příkladem velmi důležitých lineárních operátorů, operátorů rotace. Ve dvou rozměrech mají obecný tvar
kde je úhel otočení. Skutečně, dosadíme-li za hodnotu , tj. 45°, tak se tento obecný tvar matice rotace redukuje na operátor R (neboť ). Naprosto obecně, tj. i ve vyšších dimenzích, jsou rotace vyjadřovány pomocí ortogonálních operátorů, viz oddíl Lineární zobrazení vs. skalární součin.
Nakonec ještě poznamenejme, že ne všechny geometrické operace lze představovat pomocí lineárního zobrazení. Jednou z takovýchto jednoduchých geometrických operací je obyčejné posunutí vektorů. Pro posunutí musíme využít služeb obecnějších zobrazení, než jsou ta lineární. Konkrétně je nutno sáhnout k afinním zobrazením.
-
Obrázek 6: Oproti předcházejícím případům, kdy se vektory jen různě obracely či měnily svou velikost, nyní se dostáváme do zajímavější situace. Operátor D totiž svislou složku šipky dvakrát zmenší a vodorovnou složku dvakrát zvětší. Celkově to vypadá, jako by si šipky "lehaly". Lépe je působení operátoru D viditelné v pravé části, kde je vyobrazeno jeho působení na malůvku. Jak vidíme, malůvka se zplošťuje ve svislém směru a natahuje do šířky.
-
Obrázek 7: Z levé části obrázku by se dalo uhodnout, že operátor R otáčí šipky proti směru hodinových ručiček o jistý úhel. Opět zřetelněji je působení tohoto operátoru viditelné na malůvce vpravo. Skutečně se jedná o otočení vektorů proti směru hodinových ručiček a to o 45 stupňů.
Nekonečněrozměrné prostory
[editovat | editovat zdroj]Vlastnosti lineárních zobrazení definovaných na konečněrozměrných vektorových prostorech jsou pěkné a snadno se s takovýmito zobrazeními pracuje. Každé takové zobrazení lze představovat jeho maticí v nějaké bázi a veškerá práce s tímto zobrazením se redukuje na úpravu matic. V případě zobrazení definovaných na nekonečněrozměrných vektorových prostorech je ale situace složitější. Zde nelze matici zobrazení, tak jak byla definována výše, použít a celá věc se komplikuje. Příkladem lineárního zobrazení, které působí na nekonečněrozměrném vektorovém prostoru, je například derivace či integrál, viz Příklad 3. Množina lineárních zobrazení na nekonečněrozměrných prostorech je mnohem bohatší než v případě konečněrozměrných prostorů. Matematici se tak v této ohromné množině zaměřují na její jisté podmnožiny, které jsou tvořeny dostatečně pěknými zobrazeními. Cílem je vždy seskupit do jedné podmnožiny ta zobrazení, která mají společnou nějakou vlastnost, jež umožňuje, že se s těmito zobrazeními snáze pracuje.
Jednou z takových podmnožin je podmmožina tvořená omezenými lineárními zobrazeními, kterou si nyní definujeme. Uvažujme nejprve normované vektorové prostory X, Y nad týmž číselným tělesem, kde nechť je norma na prostoru X a nechť je norma na prostoru Y. Pak říkáme, že lineární zobrazení je omezené, jestliže existuje kladná konstanta taková, že pro všechny vektory platí
Pokud X=Y, nazývá se odpovídající zobrazení omezený (lineární) operátor.
Podobně jako v případě klasických lineárních zobrazení i na množině všech omezených lineárních zobrazení lze definovat jejich součet a násobení číslem. Lze dokonce ukázat, že množina všech takovýchto zobrazení tvoří vektorový prostor. Na tomto vektorovém prostoru lze navíc zavést normu omezeného lineárního zobrazení následovně
Jinými slovy je norma omezeného lineárního zobrazení rovna nejmenšímu číslu vystupujícímu v definici tohoto zobrazení, jak je podána výše.
Dále lze ukázat, že množina omezených lineárních zobrazení splývá s množinou spojitých lineárních zobrazení. Všechna ostatní lineární zobrazení, která nejsou omezená, tj. nejsou spojitá, se nazývají neomezená. Pokud použijeme výše uvedenou definici omezeného lineárního zobrazení na konečněrozměrné prostory zjistíme, že každé lineární zobrazení definované na konečněrozměrném prostoru je omezené. Na konečněrozměrných prostorech zavádět omezená zobrazení tedy nemá smysl. Na nekonečněrozměrných prostorech však tvoří omezená zobrazení malou podmnožinu všech lineárních zobrazení. Omezené operátory jsou natolik pěkná zobrazení, že pro ně platí mnoho tvrzení z případu konečněrozměrných prostorů.
Kromě omezených zobrazení a operátorů se vydělují i další speciální třídy lineárních zobrazení a operátorů definovaných na nekonečněrozměrných prostorech, jako třeba:
a další. Pro podrobnější informace viz odpovídající hesla.
Příklad omezeného operátoru
[editovat | editovat zdroj]Jako velmi triviální příklad omezeného zobrazení si uveďme operátor na prostoru kvadraticky integrabilních funkcí definovaných na intervalu . Konkrétně nechť s funkčním vztahem
kde . Jedná se tedy o zobrazení, které vezme funkci, tu zintegruje od nuly do jedničky, čímž dostane číslo, a tímto číslem pak násobí nezávisle proměnnou x. Pro konkrétní funkci f je výraz tedy lineární funkce, která je tvaru
kde je číslo závisející na funkci f. Ukažme nyní, že T je skutečně lineární omezené zobrazení. Linearita je zjevná, neboť
kde jsme využili linearity integrálu, viz Příklad 3. Ukažme nyní omezenost:
kde jsme využili rovnosti . Nyní můžeme absolutní hodnotu odhadnout pomocí známého vztahu z teorie integrálu jako
Nakonec můžeme využít Hölderovy nerovnosti (resp. Schwarzovy nerovnosti), kde položíme , abychom obdrželi vztah
kde jsme využili rovnosti . Poslední výraz je ale až na konstantu roven normě funkce f, to jest
Celkem tedy máme nerovnost
a z definice omezeného zobrazení tedy plyne, že operátor T je omezený.
Příklady
[editovat | editovat zdroj]Příklad 1 – Lineární funkce
[editovat | editovat zdroj]V oddíle Motivace výše jsme si uvedli lineární funkce jako patrně nejjednodušší příklad lineárních zobrazení. V této souvislosti je však nutno upozornit na poněkud matoucí názvosloví. Obecná lineární funkce totiž není lineární zobrazení. Jak bylo uvedeno v Motivaci, lineární funkce je lineární zobrazení právě, když má nulový absolutní člen. Neboli funkce
kde , je lineární právě, když . Z toho plyne, že přímá úměrnost je vlastně lineární zobrazení. Pokud je , tak je funkce f výše příkladem afinního zobrazení.
Příklad 2 – Matice zobrazení
[editovat | editovat zdroj]Na konečněrozměrných prostorech lze každé lineární zobrazení představovat pomocí jeho matice zobrazení. Jedná se o natolik výhodný způsob zápisu, že se při praktických výpočtech v podstatě nepracuje s ničím jiným. (Na nekonečněrozměrných prostorech je situace složitější, viz oddíl výše.) Matice daného zobrazení mění svůj tvar v závislosti na zvolené bázi. Uvažujme pro konkrétnost lineární operátor A na prostoru , jehož matice vyjádřená ve standardní bázi má tvar
Když máme vektor a chceme zjistit, jak vypadá jeho obraz při zobrazení A (tj. jak vypadá ), tak jím stačí přenásobit matici zobrazení A. Pro konkrétnost například obraz vektoru , kde
při zobrazení A vypadá následovně
Ke stejnému výsledku bychom ale dospěli i tehdy, měli-li bychom matici i vektor vyjádřeny v jiné bázi. V takovém případě je nutno místo vektoru samotného brát jeho jednotlivé souřadnice v dané bázi a těmi teprve přenásobit odpovídající matici zobrazení. Pro názornost nyní místo standardní báze uvažujme bázi tvaru
Vektor zmíněný výše lze v této bázi vyjádřit následovně:
Souřadnice vektoru v naší nové bázi jsou tedy . Pokud bychom podobně vyjádřili matici zobrazení A v této nové bázi, obdrželi bychom matici ve tvaru
O tom, jak se převádí matice zobrazení mezi bázemi, viz oddíl Matice zobrazení výše a oddíl Přechod mezi bázemi v článku Báze (lineární algebra). Zapůsobíme-li touto maticí na souřadnice vektoru , dostaneme
Sloupek za poslední rovností určuje souřadnice vektoru v bázi . Platí tedy
- .
Výsledný vektor je tedy tentýž jako když jsme počítali ve standardní bázi. Ukázali jsme tak, že ačkoli se tvar matice téhož zobrazení v různých bázích mění, výsledky jsou vždy stejné. Výběr báze tak neovlivní tvar výsledných vektorů vzniklých působením zobrazení A. V tuto chvíli si osvětleme, proč můžeme ve standardní bázi brát místo souřadnic vektoru rovnou jeho složky. Ve standardní bázi totiž platí, že souřadnice je totéž co složka vektoru. Standardní báze vektorového prostoru je tvořena následujícími třemi vektory:
Standardní báze má tu význačnou vlastnost, že souřadnice daného vektoru v této bázi je rovna jeho odpovídající složce. To lze snadno vidět, rozepíšeme-li si libovolný vektor do tvaru
Jak vidno, tak platí, že první souřadnice vektoru ve standardní bázi je rovna , jeho druhá souřadnice ve standardní bázi je rovna a konečně jeho třetí souřadnice ve standardní bázi je rovna . To v jiných bázích obecně neplatí. Když tedy chceme zjistit tvar vektoru , stačí vektorem přenásobit matici zobrazení uvedenou výše.
Příklad 3 – Derivace a integrál
[editovat | editovat zdroj]Derivování a integrování jsou velmi důležitými příklady lineárních zobrazení. V matematické analýze lze totiž dokázat, že platí následující vztahy
kde je nějaká konstanta a čísla jsou meze integrování. Pokud si označíme
tak se nám výše uvedené rovnosti redukují do tvaru
Vidíme tedy, že derivace a integrál jsou skutečně lineární zobrazení. Formálněji řečeno, derivaci lze chápat jako lineární zobrazení definované na vektorovém prostoru diferencovatelných funkcí. Uvažujme tedy množinu všech reálných funkcí reálné proměnné, které jsou diferencovatelné, tj. mají derivaci. Tuto množinu si označme , tedy
O této množině lze snadno ukázat, že tvoří vektorový prostor. Podobně lze i o množině všech reálných funkcí reálné proměnné ukázat, že je též vektorový prostor. Označme si množinu všech takovýchto funkcí jako . Množina je tedy podprostorem množiny všech funkcí . Derivace je pak zobrazení, které zobrazuje z vektorového prostoru do vektorového prostoru a je přitom lineární. Neboli
Podobné úvahy lze provézt i pro integrál. V takovém případě bereme za množinu množinu všech integrabilních funkcí. Vše ostatní je pak analogické případu pro derivaci. Derivace a integrál jsou současně i příkladem lineárních zobrazení na nekonečněrozměrných prostorech. Vektorový prostor je totiž nekonečné dimenze.
Příklad 4 – Jádro zobrazení
[editovat | editovat zdroj]V tomto příkladu si ukážeme, jak hledat jádro jednoduchých lineárních zobrazení na konečněrozměrných prostorech. Tato zobrazení lze elegantně zapisovat pomocí jejich matice. Pro konkrétnost mějme nejprve lineární operátor A na prostoru trojic čísel , jehož matice vypadá následovně (viz Příklad 2 výše)
U každé matice zobrazení je vždy nutno uvést, v jakých je vyjádřena bázích. Matice výše je vyjádřena ve standardní bázi, což je typická volba při naprosté většině aplikací. Naším úkolem je najít jádro operátoru A. Hledáme tedy takové vektory , které splňují vlastnost
Vyjádřeno ve standardní bázi:
Máme tak maticovou rovnici, jež je ekvivalentní následující soustavě rovnic:
Soustava lineárních rovnic se dá lehce vyřešit úpravou matice výše. Dostáváme
V prvním kroku jsme od třetího řádku odečetli pětinásobek prvního řádku. Ve druhém kroku jsme druhý řádek vydělili trojkou a třetí řádek vydělili sedmičkou a ve třetím kroku jsme od třetího řádku odečetli řádek druhý. V posledním kroku jsme k prvnímu řádku přičetli dvojnásobek druhého řádku. Máme tak matici vyjádřenou v horním trojúhelníkovém tvaru, ze kterého lze řešení vyčíst velmi rychle. Protože vyšel třetí řádek ze samých nul, bude jádro našeho operátoru obsahovat nenulový vektor, jak uvidíme vzápětí. Naši maticovou rovnici jsme si tak upravili do tvaru
Nulovost třetího řádku nám dovoluje zvolit složku libovolně. Z druhého řádku pak plyne a z prvního . Celkem vzato, vektor leží v jádře operátoru A právě, když je tvaru
Jádro operátoru A je tedy množina, která je rovna lineárnímu obalu tohoto vektoru
Nakonec můžeme ověřit, že na vektory daného tvaru dá zobrazení A skutečně nulový vektor. Vezmeme-li původní vyjádření matice A ve standardní bázi, máme
Skutečně tedy dostáváme nulový vektor, jak jsme chtěli.
Příklad 5 – Vlastní čísla
[editovat | editovat zdroj]Na příkladu lineárního operátoru A z předchozího příkladu si ukažme hledání jeho vlastních čísel. Zde si ukážeme jen postup, jak taková čísla najít, pro podrobnosti o námi použité metodě viz článek o vlastních číslech. Mějme tedy opět operátor A, jehož matice ve standardní bázi vypadá jako
Chceme najít všechna čísla splňující vztah
pro nějaký vektor . Pravou stranu uvedené rovnice si můžeme představit jako zobrazení působící na vektor , kde značí identitu. Výše uvedenou rovnici lze tedy přepsat do tvaru
Neboli číslo je vlastním číslem právě, když v jádře zobrazení leží nenulový vektor. V předchozím příkladě jsme hledali jádro zobrazení A, nyní chceme najít jádro zobrazení , kde vystupuje jako neznámý parametr. Můžeme tedy postupovat podobným způsobem jako v předchozím příkladě, kde nyní pracujeme s maticí pro zobrazení , jež vypadá následovně
Na konci bychom obdrželi nějaké vektory parametrizované pomocí čísla a museli bychom zjišťovat, pro které hodnoty tyto vektory skutečně leží v jádře. Existuje ale mnohem jednodušší metoda hledání vlastních čísel. V lineární algebře se dokazuje, že v jádru matice leží nenulový vektor právě, když její determinant je roven nule. Stačí tedy zjistit, pro které hodnoty čísla je . V našem případě je determinant matice pro roven
Aby byl tedy determinant nulový, tak stačí položit , nebo . Vlastní čísla operátoru A jsou tedy
Příklad 6 – Linearizace
[editovat | editovat zdroj]
Jak bylo předestřeno v úvodu článku, lineární zobrazení jsou velmi důležitá mimo jiné pro svou relativní jednoduchost. Někdy lze složité zobrazení nahradit jeho jednodušší lineární variantou. Tomuto nahrazení se říká linearizace. Typicky se tohoto postupu používá ve fyzice. Uvažujme jistou rovnici, která popisuje chování nějakého fyzikálního systému. Řešení této rovnice udává předpis, jakým se tento fyzikální systém vyvíjí. Často dochází k situaci, kdy sice známe takovou rovnici, ale nejsme ji schopni vyřešit. Důvodem mohou být funkce vystupující v rovnici, které mají příliš složitý tvar a nejsou lineární. Někdy je taková situace bezvýchodná, v jistých případech ale lze tuto složitou funkci nahradit lineární funkcí, která je té původní v jistém smyslu podobná. Dostaneme tak rovnici, v níž roli původní složité funkce nyní hraje její lineární dvojče. Tuto rovnici už můžeme vyřešit. Co nám ale řešení naší upravené rovnice přináší? Jestliže jsou dodrženy jisté podmínky, tak řešení upravené rovnice je podobné řešení původní složité rovnice. Pokud nám tedy postačí popsat daný fyzikální systém ne přesně, ale jen přibližně, tak se lze při popisu fyzikálního systému omezit na jednodušší variantu rovnice a počítat jen s ní.
Jako konkrétní případ si můžeme uvést kyvadlo. Máme závaží o hmotnosti m zavěšené na lanku délky l a zajímá nás, jak se budou kmity tohoto závaží vyvíjet s časem, zanedbáme-li tření vzduchu a další rušivé vlivy. Situaci je možno nahlédnout na obrázku vpravo. Na závaží působí tíhová síla , kde je tíhové zrychlení. Tuto sílu lze rozložit do dvou složek, viz fialové šipky na obrázku, jedna složka působí ve směru závěsu, tlačí tedy jen na závěs a na pohybu závaží se neprojeví. Druhá složka pak působí ve směru pohybu zavěšeného závaží. Z obrázku je vidět, že tato složka je rovna
kde je úhel mezi závěsem a svislicí, viz obrázek. Minus se v předchozím vztahu vyskytuje proto, že gravitační zrychlení musí mířit "dolů". (Pokud dosadíme , tak dostáváme . Kdyby tam žádné minus nebylo, tak by síla hnala závaží neustále nahoru. Ze zkušenosti ale víme, že "vše padá dolů".) Dále platí, že zrychlení závaží (ve směru jeho pohybu) je rovno
- ,
je to tedy druhá derivace úhlu podle času násobená délkou závěsu . Jak se odvodí tento vztah pro zrychlení není v tuto chvíli důležité, zajímat nás bude především následující sestavování pohybových rovnic. Newtonova pohybová rovnice zní
- ,
neboli
Jedná se o obyčejnou diferenciální rovnici druhého řádu s konstantními koeficienty. Kvůli výskytu funkce sinus ale není lineární. Nelineární diferenciální rovnice se špatně řeší. Zjednodušme si tedy počítání tím, že místo funkce vezmeme jen funkci . To lze udělat pro malé kmity, neboť pro malé hodnoty úhlu platí
a obě funkce si jsou v takovém případě dost podobné. Funkce je navíc lineární. Pohybová rovnice tedy přejde do tvaru
což lze upravit na tvar
Toto je již lineární diferenciální rovnice, kterou lze vyřešit klasickým způsobem. Tato rovnice vyjadřuje, jak se úhel mezi závěsem a svislou rovinou vyvíjí v čase. Řešení této závislosti zní
kde je počáteční úhel vychýlení kyvadla, je amplituda kmitů a je jejich úhlová frekvence.
Relativně složitou funkci sinus jsme tak v příkladu výše nahradili lineární funkcí. Pro malé úhly dávají obě funkce prakticky stejné hodnoty, pro větší úhly to už ale neplatí a náš výše vypočtený výsledek pro chování kmitů se pro velké kmity nedá použít. Spočetli jsme tak pohyb kyvadla jen v případech, kdy je amplituda kmitů malá. To je omezení, které musíme platit za to, že jsme si ulehčili práci nahrazením funkce sinus jejím lineárním dvojčetem.
Odkazy
[editovat | editovat zdroj]Literatura
[editovat | editovat zdroj]- PYTLÍČEK, Jiří. Lineární algebra a geometrie. Praha: Česká technika - nakladatelství ČVUT, 2008. ISBN 978-80-01-04063-8. – skripta FJFI ČVUT
- BALKOVÁ, Ľubomíra. Lineární algebra 1. Praha: Česká technika - nakladatelství ČVUT, 2013. ISBN 978-80-01-05346-1. – skripta FJFI ČVUT
- BLANK, Jiří; EXNER, Pavel; HAVLÍČEK, Miloslav. Lineární operátory v kvantové fyzice. Praha: Karolinum, 1993. ISBN 80-7066-586-6.
Související články
[editovat | editovat zdroj]Externí odkazy
[editovat | editovat zdroj] Obrázky, zvuky či videa k tématu lineární zobrazení na Wikimedia Commons
Obrázky, zvuky či videa k tématu lineární zobrazení na Wikimedia Commons








































































































































































































































































![{\displaystyle \scriptstyle \int _{0}^{1}|x|^{2}dx=[x^{3}/3]_{0}^{1}=1/3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2265dbb4874baaa4b1dbe04ecd5e0b0a16736dc)














































































