Spojitá funkce

Spojitá funkce je taková matematická funkce, jejíž hodnoty se mění plynule, což si lze intuitivně představit tak, že graf funkce lze nakreslit jedním tahem, aniž by se tužka zvedla z papíru. Funkce, která není spojitá, se označuje jako nespojitá.

Spojitost je také jednou ze základních vlastností požadovaných po matematických funkcích, mnoho matematických konstrukcí vyžaduje spojitost funkce jako nutnou podmínku, např. derivace, primitivní funkce apod.

Pro reálné funkce reálné proměnné lze spojitost funkce definovat následovně:

• Funkce $f$ je v bodě $a\in D(f)$ spojitá, právě když platí $\lim _{x\to a}f(x)=f(a)$.

• Funkce $f$ je na intervalu $(a,b)\subseteq D(f)$ spojitá, právě když pro každé $y\in (a,b)$ platí $\lim _{x\to y}f(x)=f(y)$.

Definice

• 
  Funkce spojitá zprava
• 
  Funkce spojitá zleva

O funkci $f:\mathbb {R} \rightarrow \mathbb {R}$ řekneme, že je spojitá v bodě $a$, pokud ke každému libovolně malému číslu $\varepsilon >0$ existuje takové číslo $\delta >0$, že pro všechna $x$, pro něž platí $|x-a|<\delta$, platí také $|f(x)-f(a)|<\varepsilon$. Velikost čísla $\delta$ může záviset nejen na volbě čísla $\varepsilon$, ale i na volbě bodu $a$.

Funkci $f$ označujeme jako spojitou zprava resp. zleva, pokud k libovolnému $\varepsilon >0$ existuje takové $\delta >0$, že pro všechna $x\in \langle a,a+\delta )$ resp. $x\in (a-\delta ,a\rangle$, tzn. pro všechna $x$ z pravého resp. levého okolí bodu $a$, platí $|f(x)-f(a)|<\varepsilon$. Funkce je spojitá tehdy, je-li spojitá zprava i zleva.

Uvedenou Cauchyho definici lze formulovat také pro funkci $n$ proměnných. O funkci $f$ o proměnných $x_{1},x_{2},...,x_{n}$ řekneme, že je spojitá v bodě $A=[a_{1},a_{2},...,a_{n}]$, pokud ke každému libovolně malému číslu $\varepsilon >0$ existuje takové číslo $\delta >0$, že pro všechny body $X=[x_{1},x_{2},...,x_{n}]$ z okolí bodu $A$, tzn. pro body jejichž vzdálenost splňuje podmínku $d(A,X)<\delta$, platí $|f(x_{1},x_{2},\ldots ,x_{n})-f(a_{1},a_{2},\ldots ,a_{n})|<\varepsilon$.

Stejnoměrná spojitost

Funkce $f:\mathbb {R} \rightarrow \mathbb {R}$ je stejnoměrně spojitá, jestliže obrazy $f(x_{1})$ a $f(x_{2})$ sobě dostatečně blízkých bodů $x_{1}$ a $x_{2}$ jsou si také dostatečně blízko a tato vlastnost nezávisí na volbě blízkých bodů, ale pouze na jejich (dostatečně malé) vzdálenosti.

Definice

• Nechť $(X,\rho )$ a $(Y,\sigma )$ jsou metrické prostory. Funkci $f:X\to Y$ nazveme stejnoměrně spojitou, pokud k libovolnému $\varepsilon >0$ existuje $\delta >0$ takové, že pro libovolné dva body $x_{1},x_{2}\in X$ platí, že pokud $\rho (x_{1},x_{2})<\delta$, tak $\sigma (f(x_{1}),f(x_{2}))<\varepsilon$.

• Mějme funkci $f:\mathbb {R} \rightarrow \mathbb {R}$ definovanou na intervalu $\langle a,b\rangle$, pro niž k libovolnému $\varepsilon >0$ existuje $\delta >0$ takové, že pro libovolné dva body $x_{1},x_{2}$ z intervalu $\langle a,b\rangle$ splňující podmínku $|x_{1}-x_{2}|<\delta$ platí $|f(x_{1})-f(x_{2})|<\varepsilon$. Pak říkáme, že funkce $f$ je stejnoměrně spojitá na intervalu $\langle a,b\rangle$.

• Mějme funkci $f:A\rightarrow \mathbb {R} ^{m}$, kde $A\subseteq \mathbb {R} ^{n}$ a $\ n,m\in \mathbb {N}$, pak říkáme, že funkce $f$ je stejnoměrně spojitá, pokud pro každou dvojici reálných posloupností $\{x_{n}\}$ a $\{y_{n}\}$ splňujících podmínku $\lim _{n\to \infty }|x_{n}-y_{n}|=0\,$ platí $\lim _{n\to \infty }|f(x_{n})-f(y_{n})|=0$.

Povšimněme si rozdílů oproti definici jen spojité funkce, konkrétně pořadí kvantifikátorů, u stejnoměrně spojité funkce hodnota $\delta$ závisí pouze na velikosti $\varepsilon$, a nikoli na bodu $x$.

Vlastnosti

• Spojitost funkce je lokální vlastnost funkce; zkoumáme, zda funkce je, či není spojitá v každém jednotlivém bodě. Pokud řekneme, že funkce je spojitá na intervalu, pak tím myslíme, že je spojitá v každém bodě tohoto intervalu. Oproti tomu stejnoměrná spojitost je vlastnost globální.
• Každá stejnoměrně spojitá funkce je spojitá.
• Složení dvou stejnoměrně spojitých funkcí je stejnoměrně spojité.
• Lipschitzovská funkce je stejnoměrně spojitá.
• Spojitá funkce na kompaktu je stejnoměrně spojitá. Speciálně každá spojitá funkce na omezeném uzavřeném intervalu je stejnoměrně spojitá.
• Pokud je reálná funkce $f$ spojitá na intervalu $\langle 0,\infty )$ a existuje vlastní limita $\lim _{x\to \infty }f(x)$, pak je funkce na intervalu $\langle 0,\infty )$ stejnoměrně spojitá.

Příklady

• Funkce $f(x)=kx$ je pro $k\in \mathbb {R}$ stejnoměrně spojitá na celé reálné ose.
• Exponenciální funkce $f(x)=e^{x}$ je spojitá na celé reálné ose, ale není na ní stejnoměrně spojitá.
• Nechť $(X,\rho )$ je metrický prostor. Pak $\rho :X\times X\to \mathbb {R}$ je stejnoměrně spojitá funkce.

Absolutní spojitost

Absolutní spojitost funkce zesiluje stejnoměrnou spojitost. Na rozdíl od ní se ale neomezuje na jeden dostatečně malý interval a velikost jeho obrazu, nýbrž klade nároky i na systémy (malých) intervalů.

Definice

Funkce $f:\mathbb {R} \rightarrow \mathbb {R}$ je absolutně spojitá na intervalu $\langle a,b\rangle$, jestliže k libovolnému $\varepsilon >0$ existuje takové $\delta >0$, že pro každý systém intervalů $\langle a_{1},b_{1}\rangle ,\langle a_{2},b_{2}\rangle ,\ldots ,\langle a_{n},b_{n}\rangle$, pro který je $a\leq a_{1}\leq b_{1}\leq a_{2}\leq b_{2}\leq \cdots \leq a_{n}\leq b_{n}\leq b$ a $\sum _{i=1}^{n}\left(b_{i}-a_{i}\right)<\delta$ platí $\sum _{i=1}^{n}\left|f\left(b_{i}\right)-f\left(a_{i}\right)\right|<\varepsilon$.

Ekvivalentní definice

Funkce $f$ je absolutně spojitá na $\langle a,b\rangle$ právě tehdy, když

• $f\in L^{1}(a,b)$ je rozdílem dvou neklesajících spojitých funkcí
• $\exists g\in L^{1}(a,b)$ taková, že $f(x)=\int _{a}^{x}g(t)\mathrm {dt} {\mbox{ }}\forall x\in (a,b)$
• $\exists h\in L^{1}(a,b)$ taková, že $|f(d)-f(c)|\leq \int _{c}^{d}h(t)\mathrm {dt} {\mbox{ }}\forall \langle c,d\rangle \subset \langle a,b\rangle$.

Pokud $f\in L^{1}(a,b)$ a $F(x)=\int _{a}^{x}f(t)\mathrm {dt}$, pak $F$ je absolutně spojitá na $\langle a,b\rangle$.

Vlastnosti

• Je-li funkce $f$ absolutně spojitá na intervalu $\langle a,b\rangle$, pak je na tomto intervalu spojitá.
• Každá absolutně spojitá funkce je stejnoměrně spojitá a tedy spojitá.
• Součet a rozdíl dvou absolutně spojitých funkcí je také absolutně spojitý.
• Lipschitzovská funkce je absolutně spojitá.
• Spojitost neimplikuje absolutní spojitost - Cantorova funkce je spojitá, ale není absolutně spojitá.
• Stejnoměrná spojitost neimplikuje absolutní spojitost - Cantorova funkce je stejnoměrně spojitá, ale není absolutně spojitá.
• Absolutně spojitá funkce $f$ má derivaci skoro všude a platí: $f(x)=f(a)+\int _{a}^{x}f'(t)\mathrm {dt} {\mbox{ }}\forall x\in \langle a,b\rangle$.

Příklady

• Funkce $f(x)=x$ je absolutně spojitá.

Polospojitost

Přesněji polospojitost shora a polospojitost zdola jsou pojmy používané v matematické analýze. Jsou to vlastnosti reálných funkcí, které jsou slabší než spojitost, nicméně dány dohromady již spojitost implikují. Každá z nich je tedy sama o sobě jen „půl spojitosti“. Funkce $f$ je shora polospojitá v bodě $x$, pokud pro body $y$ blízké bodu $x$ není $f(y)$ o moc větší než $f(x)$. Funkce $f$ je zdola polospojitá v bodě $x$, pokud pro body $y$ blízké bodu $x$ není $f(y)$ o moc menší než $f(x)$.

Definice

Shora polospojitá funkce.

• Funkce $f:X\rightarrow \mathbb {R}$, kde $X$ je topologický prostor, je shora polospojitá v bodě $x\in X$, pokud pro každé $\varepsilon >0$ existuje okolí $U$ bodu $x$ tak, že pro každé $y\in U$ platí $f(y)<f(x)+\varepsilon$.

• Funkce $f$ je shora polospojitá v $X$ , jestliže je shora polospojitá v každém bodě $x\in X$. Je to právě tehdy, když jsou všechny množiny tvaru $\{x\in X:f(x)<\varepsilon \}$ otevřené.

Ekvivalentně můžeme říci, že $f$ je shora polospojitá v bodě $x$, pokud $\limsup _{y\to x}f(y)\leq f(x)$.

Zdola polospojitá funkce.

• Funkce $f:X\rightarrow \mathbb {R}$, kde $X$ je topologický prostor, je zdola polospojitá v bodě $x\in X$, pokud pro každé $\varepsilon >0$ existuje okolí $U$ bodu $x$ tak, že pro každé $y\in U$ platí $f(y)>f(x)-\varepsilon$.

• Funkce $f$ je zdola polospojitá v $X$ , jestliže je zdola polospojitá v každém bodě $x\in X$. Je to právě tehdy, když jsou všechny množiny tvaru $\{x\in X:f(x)>\varepsilon \}$ otevřené.

Ekvivalentně můžeme říci, že $f$ je zdola polospojitá v bodě $x$, pokud $\liminf _{y\to x}f(y)\geq f(x)$.

Vlastnosti

• Nerovnost $\limsup _{y\to x}f(y)\leq f(x)\leq \liminf _{y\to x}f(y)$ ukazuje, že pokud je $f$ v bodě $x$ polospojitá shora i zdola, je již v bodě $x$ spojitá.
• Nerovnost $\limsup _{y\to x}f(y)\geq f(x)\geq \liminf _{y\to x}f(y)$ ukazuje, že pokud je $f$ v bodě $x$ polospojitá shora i zdola, je již v bodě $x$ spojitá.
• Funkce $f$, která je shora polospojitá na kompaktním prostoru $X$, je již nutně shora omezená na $X$ a má na $X$ maximum.
• Funkce $f$, která je zdola polospojitá na kompaktním prostoru $X$, je již nutně zdola omezená na $X$ a má na $X$ minimum.
• Protože $\{\sup _{f\in {\mathcal {F}}}f>a\}=\bigcup _{f\in {\mathcal {F}}}\{f>a\}$, je supremum libovolného systému zdola polospojitých funkcí ${\mathcal {F}}$ opět zdola polospojité.
• Protože $\{\sup _{f\in {\mathcal {F}}}f>a\}=\bigcup _{f\in {\mathcal {F}}}\{f>a\}$, je infimum libovolného systému shora polospojitých funkcí ${\mathcal {F}}$ opět zdola polospojité.
• Naopak supremum shora polospojitých (nebo dokonce spojitých) funkcí nemusí být shora polospojité, jak ukazuje příklad ${\mathcal {F}}=\{\arctan(n\cdot ):n\in \mathbb {N} \}$.
• Norma na Banachově prostoru $X$ je slabě polospojitá zdola (tedy zdola polospojitá na topologickém prostoru $(X,w)$). Je-li dimenze $X$ nekonečná, norma nemůže být slabě polospojitá shora, tedy ani slabě spojitá.

Příklady

• Charakteristická funkce otevřené množiny je zdola polospojitá.
• Charakteristická funkce uzavřené množiny je shora polospojitá.

Spojitost komplexní funkce

Komplexní funkce $f:\mathbb {C} \rightarrow \mathbb {C}$ je spojitá v bodě $z_{0}$ části komplexní roviny $\mathbf {\Omega }$, na které je definovaná, jestliže platí:

$\lim _{z\rightarrow z_{0}}f(z)=f(z_{0})$.

Je-li funkce $f(z)$ spojitá v každém bodě oblasti $\mathbf {\Omega }$, pak říkáme, že je spojitá na oblasti $\mathbf {\Omega }$.

Věty o spojitosti

• Heineho věta říká, že funkce $f$ definovaná na prstencovém okolí bodu $a$ je v bodě $a$ spojitá, právě když pro každou posloupnost čísel $\{x_{n}\}_{n=1}^{\infty }$ z uvedeného okolí bodu $a$ takovou, že $x_{n}\neq a$ a $\lim _{n\to \infty }x_{n}=a$ platí $\lim _{n\to \infty }f(x_{n})=f(a)$.
• Weierstrassova věta říká, že je-li funkce $f$ spojitá na uzavřeném intervalu $\langle a,b\rangle$, pak na intervalu $\langle a,b\rangle$ existuje alespoň jeden bod $x_{1}\in \langle a,b\rangle$ takový, že $f(x_{1})\geq f(x)$ pro všechna $x\in \langle a,b\rangle$. Jedná se o maximum funkce $f$ na intervalu $\langle a,b\rangle$. Současně také existuje alespoň jeden bod $x_{2}\in \langle a,b\rangle$ takový, že $f(x_{2})\leq f(x)$ pro všechna $x\in \langle a,b\rangle$. Jedná se o minimum funkce $f$ na intervalu $\langle a,b\rangle$. Funkce spojitá na uzavřeném intervalu $\langle a,b\rangle$ je tedy na tomto intervalu také ohraničená.
• Weierstrassova aproximační věta říká, že máme-li funkci $f$ spojitou na intervalu $\langle a,b\rangle$, pak pro každé $\varepsilon >0$ existuje polynom $P$ takový, že $|f(x)-P(x)|<\varepsilon$ pro všechna $x\in \langle a,b\rangle$.
• Bolzanova věta říká, že je-li funkce $f$ spojitá na uzavřeném intervalu $\langle a,b\rangle$ a splňuje-li podmínku $f(a)f(b)<0$, pak existuje alespoň jeden bod $c\in \langle a,b\rangle$ takový, že $f(c)=0$.
• Darbouxova věta říká, že je-li funkce $f$ spojitá na uzavřeném intervalu $\langle a,b\rangle$, pak pro $m=\min\{f(x)|x\in \langle a,b\rangle \}$ a $M=\max\{f(x)|x\in \langle a,b\rangle \}$ platí $f(\langle a,b\rangle )=\langle m,M\rangle$, tj. ke každému $y_{0}\in \langle m,M\rangle$ existuje $x_{0}\in \langle a,b\rangle$ tak, že $f(x_{0})=y_{0}$.

Poznamenejme, že v anglické a francouzské matematické literatuře se pod pojmem Darbouxova věta rozumí většinou věta říkající, že derivace diferencovatelné funkce na otevřeném intervalu má tzv. vlastnost nabývání mezihodnot. V části ruské matematické literatury se pod pojmem Darbouxova věta rozumí věta uvedená v předchozím odstavci.

Body nespojitosti

Body, v nichž daná funkce není spojitá, označujeme jako body nespojitosti:

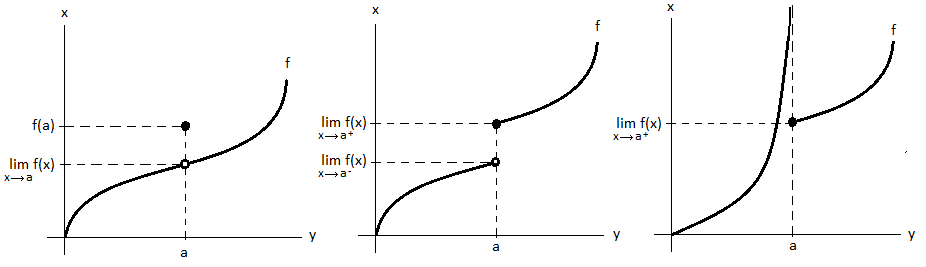
Pokud v bodě $a$ existuje vlastní oboustranná limita, avšak je různá od funkční hodnoty v bodě $a$, tj. $\lim _{x\to a}f(x)\neq f(a)$, pak v bodě $a$ nastává odstranitelná nespojitost funkce $f$, funkci lze v bodě $a$ předefinovat.

Bod nespojitosti prvního druhu funkce $f$ - takový bod $a$, v němž existují obě vlastní limity zprava i zleva, avšak tyto limity mají rozdílné hodnoty, tj. $\lim _{x\to a+}f(x)\neq \lim _{x\to a-}f(x)$. Rozdíl mezi těmito čísly, tj. $|\lim _{x\to a+}f(x)-\lim _{x\to a-}f(x)|$, nazýváme skokem funkce v bodě $a$.

Bod nespojitosti druhého druhu funkce $f$ - takový bod $a$, v němž neexistuje alespoň jedna z vlastních jednostranných limit.

Funkci, která je definována na intervalu $\langle a,b\rangle$, označíme jako po částech spojitou, je-li spojitá ve všech bodech intervalu s výjimkou konečného počtu bodů, v nichž má nespojitost prvního druhu.

Vlastnosti

• Má-li funkce $f(x)$ v bodě $a$ konečnou derivaci, pak je v bodě $a$ také spojitá.
• Pokud je funkce $f(x)$ spojitá v bodě $a$ a funkce $g(y)$ spojitá v bodě $b=f(a)$, pak složená funkce $g(f(x))$ je spojitá v bodě $a$.

Příklady

Funkce dolní celá část, nespojitá v každém celém čísle

• Všechny polynomické funkce, exponenciální funkce, sinus a kosinus a funkce absolutní hodnota jsou spojité v celém oboru reálných čísel.
• Racionální funkce, logaritmy, tangens a kotangens jsou spojité na svém definičním oboru (ale nejsou definované pro všechna reálná čísla). Obecněji, všechny elementární funkce jsou spojité v každém bodě svého definičního oboru.
• Funkce signum (znaménko) je nespojitá v bodě x = 0. I velmi malá změna hodnoty kolem tohoto bodu způsobí velkou změnu hodnoty: sgn −0,001 = −1, ale sgn 0,001 = 1. V tomto bodě je bod nespojitosti prvního druhu. Funkce má skok o velikosti 2.
• Funkce pro získání nejbližšího menšího celého čísla je nespojitá v každém celém čísle. V každém z těchto bodů je bod nespojitosti prvního druhu se skokem o velikosti 1.
• Extrémním příkladem je tzv. Dirichletova funkce, která je definovaná pro všechna reálná čísla, ale v žádném bodě není spojitá. Tato funkce má v každém bodě bod nespojitosti druhého druhu.
• Funkce ${\frac {\sin x}{x}}$ není definovaná v bodě $x=0$ a má zde konečnou limitu $\lim _{x\to 0}{\frac {\sin x}{x}}=1.$ Jedná se tedy o odstranitelnou nespojitost. Spojitým dodefinováním funkční hodnoty v počátku vznikne funkce sinc.

Literatura

• BARTSCH, Hans-Jochen. Matematické vzorce. 4. vyd. Praha: Academia, 1994. 832 s. ISBN 80-200-1448-9. 

• JARNÍK, Vojtěch. Diferenciální počet I. 7. vyd. Praha: Academia, 1984. 392 s. 

Související články

• Funkce
• Komplexní funkce
• Spojité zobrazení
• Okolí

Portály: Matematika