Magnetické pole
Magnetické pole je fyzikální pole, jehož zdrojem je pohybující se elektrický náboj, tj. elektrický proud. Magnetické pole lze tedy pozorovat kolem elektrických vodičů, kde je zdrojem pole volný elektrický proud, ale také kolem tzv. permanentních magnetů, kde jsou zdrojem pole vázané elektrické proudy. Magnetické pole může být také vyvoláno změnami elektrického pole.
V případě časově neměnného magnetického pole, v němž se nevyskytují volné elektrické proudy, mluvíme o magnetostatickém poli. Magnetické pole je dílčím projevem obecného elektromagnetického pole, na elektrickém poli je nezávislé pouze magnetostatické pole.
Podle prostorového rozložení magnetické indukce dělíme magnetické pole na homogenní a nehomogenní pole. Homogenní magnetické pole je v dané oblasti prostoru takové magnetické pole, jehož magnetická indukce je ve všech bodech této oblasti shodná velikostí i směrem. Lze jej znázornit přímými, rovnoběžnými, stejně od sebe vzdálenými indukčními čarami.
Speciálním případem magnetického pole je stacionární magnetické pole, jehož makroskopické veličiny nezávisí na čase. Zatímco v případě magnetostatického pole jsou volné proudy nulové, u stacionárního magnetického pole mohou být tyto proudy nenulové, avšak musí být konstantní. Volné proudy se tedy nemění v čase (takové proudy vznikají např. při rovnoměrném přímočarém pohybu elektrických nábojů). Stacionární magnetické pole se tedy vyskytuje v okolí vodičů s konstantním proudem a nepohybujících permanentních magnetů. Nestacionární magnetické pole způsobuje vznik vírového elektrického pole.
Síla magnetického pole
[editovat | editovat zdroj]
Lorentzova síla je projevem elektromagnetického pole na hmotu, působí na náboj částice pohybující se rychlostí :
- ,
běžně je jako Lorentzova síla označován pouze příspěvek magnetické síly:
- ,
při zanedbání příspěvku elektrické síly ,
kde je intenzita elektrického pole, je magnetická indukce a vyjadřuje vektorový součin. Rozdělení magnetických a elektrických příspěvků je závislé na vztažné soustavě.
Elektrický proud je pohyb rovnoměrně rozloženého náboje, proto magnetická síla působí rovněž na vodič jímž protéká elektrický proud. Toto silové působení lze odvodit z výrazu:
- ,
kde a , který následně integrujeme:
- ,
kde je proud protékající vodičem zanedbatelného průřezu, je parametrická křivka odpovídající tvaru vodiče orientovaná ve směru proudu, přes kterou integrujeme a je orientovaný element její délky. Tento vztah se nazývá Ampérův zákon pro magnetickou sílu. V případě, že je magnetické pole homogenní a křivka tvoří úsečku délky , lze tento zákon zjednodušit na tvar:
- .
Práce magnetického pole
[editovat | editovat zdroj]Elementární práci magnetického pole vykonanou na přemístění smyčky vodiče délky protékaného proudem v magnetickém poli o indukci po dráze vyjádříme vztahem:
- ,
kde je elementární změna magnetického indukčního toku procházejícího smyčkou. Práce magnetického pole na přemístění smyčky bude kladná, když tok poroste, neboť magnetické síly mají tendenci vtahovat smyčku do silnějšího pole.
Při polním popisu platí pro elementární hustotu práce konané magnetickým polem vztah:
- , kde je intenzita magnetického pole.
Práce magnetického pole o magnetické indukci na zmagnetování látky lze vyjádřit (obdobně jako u polarizace):
- ,
kde je vzniklý (Ampérův) magnetický dipólový moment.
Pro elementární hustotu práce pak platí vztah:
- ,
kde je magnetizace.
Intenzita magnetického pole
[editovat | editovat zdroj]| Intenzita magnetického pole | |
|---|---|
| Název veličiny a její značka | Intenzita magnetického pole H |
| Hlavní jednotka SI a její značka | ampér na metr A·m−1 |
| Definiční vztah | |
| Dle transformace složek | vektorová |
| Zařazení jednotky v soustavě SI | odvozená |
Intenzita magnetického pole je vektorová fyzikální veličina popisující míru silových účinků magnetického pole. Její jednotka SI je ampér na metr, značka . Na rozdíl od magnetické indukce nezahrnuje vliv vázaných elektrických proudů, ale pouze vliv volných elektrických proudů. Základním obecným vztahem pro intenzitu stacionárního magnetického pole buzeného ustáleným volným elektrickým proudem je Ampérův zákon:
- ,
kde integrace probíhá podle délky libovolně zvolené uzavřené křivky obemykající volný elektrický proud. V oblastech prostoru, kde lze považovat prostorové rozložení elektrického proudu za spojité (v makroskopickém smyslu), popsatelné hustotou elektrického proudu, lze Ampérův zákon přepsat do diferenciálního tvaru:
- .
V nestacionárním poli pak platí první Maxwellova rovnice, která je definičním vztahem pro intenzitu magnetického pole v soustavě SI:[1]
resp. v diferenciálním tvaru:
- .
kde je obsah plochy ohraničené křivkou a je elektrická indukce.
Vztah k magnetické indukci dostaneme ve tvaru:
- ,
kde je magnetizace charakterizující účinky vázaných elektrických proudů.
Intenzitu stacionárního magnetického pole vytvořeného lineárním vodičem protékaným proudem udává Biotův–Savartův zákon:
- ,
kde integrace probíhá přes všechny body křivky vodiče resp. pro spojitě rozložený proud s hustotou :
- ,
kde integrace probíhá přes všechny body oblasti protékané proudem.
Vzhledem k tomu, že intenzita magnetického pole je definována pomocí první Maxwellovy rovnice, vyplývají pro ni podobná omezení jako pro tuto rovnici. Polarizační proudy jsou započteny na pravé straně rovnice, naopak magnetizační na levé straně (skryté v intenzitě magnetického pole). Ve velmi rychle proměnném elektromagnetickém poli však nelze vázané proudy rozdělit na posuvné polarizační a uzavřené magnetizační proudy, neboť podstatné změny pole proběhnou za kratší čas, než je charakteristický čas pro uzavření magnetizačního proudu. V takovém případě se všechny vázané proudy jeví jako polarizační a magnetizaci, a tedy ani intenzitu magnetického pole, nelze rozumně definovat. I polarizace a elektrická indukce tím získávají odlišný charakter. Elektromagnetické pole se pak zpravidla popisuje pomocí tří vektorových veličin: intenzity elektrického pole, magnetické indukce a oné pozměněné elektrické indukce, pro které se formulují pozměněné Maxwellovy rovnice.[2]
K popisu magnetického pole se používá také intenzita magnetického pole. Tato historicky starší veličina vznikla ve fluidové teorii magnetismu jako obdoba intenzity elektrického pole, nahrazením náboje magnetickým množstvím. Skutečnou fyzikální souvislost s magnetickou indukcí lze zapsat vztahem:
- .
Ve vakuu jsou obě veličiny souhlasné a jejich velikosti a fyzikální rozměry se liší pouze o multiplikativní konstantu, permeabilita vakua. Rozdíl však je podstatný v látkovém prostředí. Intenzita magnetického pole popisuje magnetické pole, jako by bylo vytvářeno pouze volnými proudy.[pozn. 1] Diametrálně se pak obě veličiny liší v prostředích s permanentní magnetizací bez volných proudů, kdy mohou mít úplně opačný směr a pole jimi popsaná mají jiný charakter (vírové u indukce a zřídlové u intenzity). V elektrotechnických aplikacích je někdy praktické oba přístupy popisu pole kombinovat, např. popisovat vnější magnetické pole cívky s jádrem pomocí intenzity a pole uvnitř jádra pak pomocí indukce.
Z historických důvodů, od doby, kdy magnetismus byl vysvětlován fluidovou teorií, odpovídají pojmy a vztahy mezi intenzitou magnetického pole a magnetickou indukcí stacionárního magnetického pole obdobným vztahům z elektrostatiky mezi intenzitou elektrického pole a elektrickou indukcí. Tato analogie je pouze formální, nikoli fyzikální. Ve skutečnosti jsou základními vektory polí intenzita elektrického pole a magnetická indukce, popisující skutečné silové účinky celkového pole v prostředí. Intenzita magnetického pole je pak obdobná elektrické indukci, neboť obě odhlížejí od účinků dodatečných polí vzniklých v prostředí a popisují pole jako účinky pouze volných proudů resp. volných nábojů. Obě tyto veličiny tak doplňují popis polí v látkovém prostředí a jsou výhodné pro praktické výpočty vzhledem ke svému bezprostřednějšímu vztahu k makroskopickým zdrojům polí.[3][4] Dokládá to např. výše uvedený Biotův–Savartův zákon, který umožňuje výpočet magnetického pole elektrického proudu, aniž by byla nutná znalost magnetických vlastností prostředí.
Magnetická indukce
[editovat | editovat zdroj]| Magnetická indukce | |
|---|---|
| Název veličiny a její značka | Magnetická indukce B |
| Hlavní jednotka SI a její značka | tesla T |
| Definiční vztah | |
| Dle transformace složek | vektorová |
| Zařazení jednotky v soustavě SI | odvozená |
Magnetická indukce je vektorová fyzikální veličina, jejíž vektorový součin s proudovým elementem se rovná síle, kterou magnetické pole působí na tento element.[5] Vyjadřuje silové účinky magnetického pole na pohybující se částici s nábojem nebo magnetickým dipólovým momentem. Jednotkou je tesla, značka . Magnetická indukce není vektorem pravým, ale tzv. axiální vektor, protože její směr se nemění při prostorové inverzi souřadnic. Hodnota vektoru magnetické indukce obecně závisí na poloze v prostoru, takže tvoří vektorové pole. S magnetickou indukcí souvisí vektorová veličina intenzity magnetického pole, taktéž používaná k popisu magnetického pole, která však může mít v látkovém prostředí velmi odlišný charakter. Homogenní magnetické pole má magnetickou indukci 1 tesla, působí-li na přímý vodič s aktivní délkou 1 metr kolmý k indukčním čárám a protékaný stálým proudem 1 ampér silou 1 newton.
Pohybuje-li se bodový náboj rychlostí v daném bodě magnetického pole určeném polohovým vektorem po dráze délky , obecně na něj působí magnetická síla , jejíž velikost závisí kromě jiného i na směru pohybu náboje. Velikost magnetické indukce v bodě lze definovat jako velikost maximální (přes směr pohybu náboje) síly působící na tento náboj, která připadá na jednotkovou hodnotu . Směr vektoru je pak definován jako směr kolmý jak ke směru pohybu náboje tak k působící síle . Tímto je až na orientaci určena magnetická indukce v daném bodě . Orientace vektoru je tedy zvolena tak, aby platila uvedená rovnice. Vztah mezi orientací magnetické indukce a magnetické síly je proto dán výše uvedeným vektorovým součinem. Pro infinitezimální přírůstek síly dostaneme vztah:
- , neboť .
Integrací vztahu dostaneme:
- ,
kde je proud protékající vodičem zanedbatelného průřezu, je parametrická křivka odpovídající tvaru vodiče orientovaná ve směru proudu, přes kterou integrujeme a orientovaný element její délky. Tento vztah se nazývá Ampérův zákon pro sílu v magnetickém poli. V případě, že je magnetické pole homogenní a úsek vodiče v něm umístěný je přímý (rovný), lze tento zákon zjednodušit na tvar:
- , pak pro stacionární situaci platí: ,
kde je délka úseku vodiče.
Magnetický indukční tok
[editovat | editovat zdroj]
Magnetický indukční tok slouží pro kvantitativní popis sumárního působení magnetického pole s daným rozložením, například při jevu elektromagnetické indukce. Vyjadřuje úhrnný tok magnetické indukce procházející určitou souvislou plochou. Jednotkou je weber, . Při názorném zobrazení pomocí indukčních čar je mírou celkového počtu indukčních čar procházejících touto plochou.
Magnetický indukční tok vytvářený magnetickou indukcí na libovolně orientované ploše je definován:
- .
Je-li magnetické pole homogenní a plocha rovinná, pak platí:
- ,
kde je úhel, který svírá normálový vektor plochy s vektorem magnetické indukce.
Magnetický tok libovolnou uzavřenou plochou je nulový:
- ,
resp. v diferenciálním tvaru:
- ,
tyto vztahy jsou vyjádřením skutečnosti, že v přírodě nebyly pozorovány žádné magnetické náboje označované jako magnetické monopóly, které by byly zdrojem magnetického pole. Důsledkem neexistence magnetických monopólů je také skutečnost, že magnetické indukční čáry jsou vždy uzavřenými křivkami.
Magnetická indukce generovaná pouze volným uzavřeným elektrickým proudem je podle Biotova–Savartova zákona přímo úměrná velikosti tohoto proudu. Z toho plyne ve stacionárním případě obdobná úměrnost i pro magnetický indukční tok. Platí to i pro nejjednodušší případ rovinné smyčky tenkého vodiče protékaného proudem :
- ,
kde je indukčnost. Indukčnost je pomocí tohoto vztahu definována.[6] Magnetický indukční tok je vhodnou veličinou pro popis jevu elektromagnetické indukce. Ve smyčkách vodičů se v proměnném magnetickém poli indukují elektromotorická napětí:[7]
- .
Magnetická polarizace
[editovat | editovat zdroj]Magnetická polarizace představuje objemovou hustotu magnetického dipólového momentu. Jednotkou je tesla, . Coulombův magnetický dipólový moment byl zaveden na základě historických představ o magnetismu vyvolávaném magnetickými množstvími (obdoba nábojů) analogicky elektrickému dipólovému momentu. Od magnetizace se liší koeficientem rovným permeabilitě vakua v prostředí:
- ,
nebo ekvivalentně:[1]
- ,
vztah pro magnetickou indukci pak lze zapsat ve tvaru:
- .
Magnetický dipól
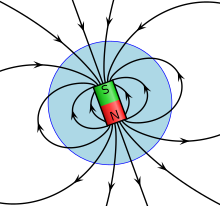
[editovat | editovat zdroj]Magnetický dipól je předmět, který kolem sebe vytváří magnetické pole podobné poli elektrického dipólu. Jako dipól můžeme chápat běžný permanentní magnet se severním a jižním pólem, odtud název dipól. Dipólový charakter má také pole vodivé smyčky, kterou protéká elektrický proud a (s omezenou přesností) i magnetické pole Země a některých dalších planet.
Dipólový moment
[editovat | editovat zdroj]Magnetický dipól je charakterizován vektorovou fyzikální veličinou, tj. magnetickým dipólovým momentem (analogicky je elektrický dipól popsán elektrickým dipólovým momentem), který můžeme určit ze vztahu:
- ,
kde je proud procházející smyčkou dipólu a je orientovaná plocha smyčkou dipólu ohraničená. Vektor je orientován kolmo k rovině smyčky dipólu a z rovnice je vidět, že stejný směr má i vektor dipólového momentu. Změní-li se směr proudu ve smyčce, obrátí se vektor na opačnou stranu.
Orientace ve vnějším poli
[editovat | editovat zdroj]Volný dipól vložený do vnějšího magnetického pole se vlivem magnetické síly natáčí tak, aby dipólový moment mířil stejným směrem jako magnetická indukce pole. Proto se například magnety volně položené na stůl blízko sebe zorientují souhlasně, čili opačnými póly k sobě. Ze stejného důvodu se železné piliny v prostoru kolem magnetu zorientují ve směru magnetických indukčních čar. Při souhlasné orientaci má totiž dipól nejmenší potenciální energii, kterou lze vyjádřit rovnicí:
- ,
kde značí skalární součin, je úhel mezi vektory a . Z tohoto vztahu lze určit také práci potřebnou k pootočení dipólu. Na dipól působí magnetická síla:
- ,
kde je operátor nabla. Tato síla má posuvné účinky. Způsobuje, že magnety se přitahují opačnými póly k sobě, zatímco souhlasné póly se odpuzují. Ze vztahu je ovšem vidět, že v homogenním poli je výsledná síla nulová a dipól se pouze natáčí. Otáčivé účinky vnějšího pole na dipól můžeme vyjádřit jako moment magnetické síly:
- ,
kde značí vektorový součin. Je vidět, že síla neotáčí dipól orientovaný souhlasně s polem, protože moment je nulový. V této orientaci má potenciální energie minimum, takže jde o stabilní rovnovážnou polohu. Moment je nulový i pro dipól orientovaný opačně, ovšem tato rovnováha je labilní (maximum potenciální energie).
Pole elementárního dipólu
[editovat | editovat zdroj]Jsou-li rozměry smyčky či magnetu výrazně menší než vzdálenost, v níž magnetické pole zkoumáme, můžeme místo skutečného dipólu uvažovat tzv. elementární dipól (též bodový dipól). Vektorový potenciál bodového dipólu s momentem umístěného v počátku souřadné soustavy je dán vztahem:
- ,
kde je polohový vektor a je permeabilita vakua. Potenciál má tedy směr kolmý na i (víří kolem osy dipólu) a velikost:
- .
Magnetická indukce, která charakterizuje silové účinky pole, je svázána s potenciálem rovnicí:
- .
Z ní lze po úpravách získat vztah pro indukci v místě dostatečně vzdáleném od dipólu:
- ,
kde je úhel mezi a , resp. jsou jednotkové vektory ve směru resp. . Velikost indukce ubývá se třetí mocninou vzdálenosti. V rovině „rovníku“ je první člen nulový, takže indukce má směr opačný k . Na ose dipólu má indukce směr shodný s dipólovým momentem.
Magnetický monopól
[editovat | editovat zdroj]Magnetický monopól je hypotetická elementární částice, která nese magnetický náboj. Existenci této částice předpovídá více teorií fyziky částic, zejména teorie velkého sjednocení a teorie superstrun. Z hlediska teorie by zdrojem magnetického pole nemusel být pouze elektrický proud, ale mohl by jím být také tzv. magnetický náboj, který by kolem sebe vytvářel magnetické pole podobným způsobem jako kolem sebe elektrický náboj vytváří elektrické pole. Tyto magnetické náboje (tzv. magnetické monopóly) však nebyly nikdy pozorovány a předpokládá se, že v přírodě neexistují. Navzdory vícero experimentům se jejich existence nepotvrdila, takže je stále možné, že magnetické monopóly neexistují. Byly ale prokázány kvazičástice, které se částečně jako magnetický monopól chovají, což zdvihlo určitou vlnu mediálního zájmu.[8]
Vznik magnetického pole
[editovat | editovat zdroj]Pohybující se elektrický náboj nejen podléhá silovým účinkům magnetického pole, ale také toto pole vytváří. Magnetické pole však nevzniká pouze při pohybu elektrického náboje, ale také při změně elektrického pole. Elektrické a magnetické pole jsou dvě tváře elektromagnetického pole a to je souhrnně popsáno Maxwellovými rovnicemi spolu s materiálovými vztahy. Ke vzniku magnetického pole se vztahují první a čtvrtá Maxwellova rovnice. První rovnice popisuje zdroje pole a čtvrtá rovnice vyjadřuje skutečnost, že neexistují žádné magnetické náboje a tedy, že magnetické pole je výhradně pole vírové. První Maxwellova rovnice však nepoužívá jako veličinu popisující magnetické pole magnetickou indukci, nýbrž intenzitu magnetického pole, která je s magnetickou indukcí spjata vztahem:
- ,
kde je permeabilita vakua a je magnetizace, vyjadřující příspěvek prostředí k výslednému magnetickému poli. Jednou z elementárních možností vzniku magnetického pole (v tomto případě nestacionárního) je pohyb bodového elektrického náboje konstantní rychlostí, takto vznikající magnetické pole lze vyjádřit vztahem:
- ,
kde je rychlost pohybu bodového náboje vůči bodu , je intenzita elektrického pole tohoto náboje v bodě , je permeabilita vakua a je permitivita vakua. Označíme-li velikost tohoto náboje a jeho polohu jako , potom elektrickou intenzitu vytvářenou nábojem v bodě vyjadřuje rovnice:
- .
Po dosazení této rovnice do výše uvedeného vztahu pro magnetickou indukci dostaneme takzvaný Biotův–Savartův zákon pro bodový náboj:
- .
Obdobným způsobem, jaký je použit výše na odvození vztahu pro magnetickou sílu působící na vodič s proudem, lze z Biotův–Savartova zákona pro bodový náboj odvodit Biotův–Savartův zákon v základní podobě:
- ,
kde je permeabilita prostředí, kterým může být vakuum nebo lineární homogenní magnetikum, je proud protékající vodičem zanedbatelného průřezu, jehož tvar (po zanedbání průřezu) tvoří křivku , které odpovídá parametrická křivka orientovaná ve směru protékajícího proudu.
Makroskopické magnetické pole může existovat ve vakuu i v látce. Magnetické pole působí na vodiče protékané elektrickým proudem, na nabitá tělesa, která se pohybují, ale také na látky, které jsou v klidu. Magnetické pole se popisuje pomocí magnetické indukce a intenzity magnetického pole.
Vznik točivého magnetického pole
[editovat | editovat zdroj]
Točivé magnetické pole je takové pole, které spojitě mění svůj směr působení ve smyslu rovnoměrného otáčivého pohybu vektoru magnetické indukce kolem své osy. Točivé magnetické pole lze mechanicky vytvořit rovnoměrným otáčením permanentního magnetu či elektromagnetu (cívky protékané stejnosměrným proudem) zvaného rotor kolem jeho osy, indukujícího elektrické napětí ve třech cívkách umístěných na statoru generátoru, vzájemně pootočených o 120°, tj. mechanická energie se mění v elektromagnetickou. Takto vytvořené točivé magnetické pole generované ve statoru motoru pak naopak roztáčí jeho rotor, tj. mění elektromagnetickou energii v mechanickou. Točivé elektomagnetické pole je hlavním důvodem přenosu elektrického výkonu právě trojfázovou soustavou.
Magnetické indukční čáry
[editovat | editovat zdroj]
Tvar pole lze popsat magnetickými indukčními čárami. Jsou to uzavřené neprotínající se orientované křivky, jejichž tečna v daném bodě má směr vektoru magnetické indukce a jejichž hustota (počet čar procházejících skrz jednotkový kolmý element plochy) je úměrná velikosti vektoru magnetické indukce. Volně otáčivá úzká magnetka (stejně jako zmagnetovaná podlouhlá železná pilina na obrázku vpravo) či cívka protékaná elektrickým proudem vložená do pole se tedy ustálí tak, že jejich osa bude tečnou k indukčním čárám magnetického pole v tomto bodě (za předpokladu, že jejich velikost není větší než oblast, ve které lze pole považovat za homogenní). Podle zvyklosti, vycházející z obdoby s magnetickým polem Země, se někdy oblast tělesa (magnetu), ze které směřuje vektor magnetické indukce ven z tělesa označuje jako severní pól (a značí anglickým N či méně často českým S) a oblast kde vektor magnetické indukce směřuje dovnitř tělesa jižní pól (a značí anglickým S či méně často českým J). Toto označení je založeno na zastaralé představě o magnetickém poli jako poli magnetických nábojů (monopólů).

Ampérovo pravidlo pravé ruky popisuje orientaci magnetických indukčních čar při průchodu elektrického proudu přímým vodičem, popřípadě cívkou. Je pojmenováno po André-Marie Ampèrovi.
Jestliže palec pravé ruky ukazuje směr elektrického proudu ve vodiči, pak pokrčené prsty ukazují orientaci magnetických indukčních čar.
Z tohoto pravidla lze snadno odvodit Ampérovo pravidlo pravé ruky pro cívku, které zní následovně:
Cívku uchopíme do pravé ruky tak, že ohnuté prsty ukazují směr elektrického proudu v jejích závitech. Odtažený palec pak ukazuje severní pól cívky.
Jiná, aplikovaná verze Ampérova pravidla pravé ruky praví: Když položíme na drát pravou ruku ve směru proudu, sever střelky se po zapnutí proudu odkloní ve směru palce. Napřed je ale dobré zorientovat obvod tak, aby proud tekl od jihu k severu.

Flemingovo pravidlo levé ruky používáme k určení směru magnetické síly, která působí na vodič v magnetickém poli. Je pojmenováno po J. A. Flemingovi. Flemingovo pravidlo levé ruky umožňuje určit směr síly, kterou působí vnější magnetické pole na vodič, který se v tomto poli nachází. Toto pravidlo říká, že pokud prsty ukazují směr proudu a indukční čáry vnějšího magnetického pole vstupují do dlaně, pak palec ukazuje směr síly, kterou působí vnější magnetické pole na vodič s proudem:
Položíme-li otevřenou dlaň levé ruky na vodič, kterým protéká proud, tak aby prsty ukazovaly směr proudu a indukční čáry vstupovaly do dlaně, odtažený palec ukazuje směr síly, kterou působí magnetické pole na vodič.
nebo:
Pokud prsty ukazují směr proudu a indukční čáry vnějšího magnetického pole vstupují do dlaně, pak palec ukazuje směr síly, kterou působí vnější magnetické pole na vodič s proudem.
Zobrazení magnetického pole
[editovat | editovat zdroj]Ke znázornění magnetického pole můžeme využít magnetické indukční čáry.[9] Magnetická indukční čára je vždy uzavřená křivka, jejíž tečna má v daném bodě směr osy malé magnetky umístěné v tomto bodě. U přímého vodiče tak pozorujeme soustředné kružnice se středem v místě průsečíku vodiče s rovinou na něj kolmou, ve které kružnice leží.[10]
Uvnitř cívky jsou magnetické indukční čáry navzájem rovnoběžné s osou cívky. Vně cívky je magnetické pole obdobné jako u tyčového magnetu. Magnetické indukční čáry zde vytváří uzavřené křivky vystupující z jednoho konce cívky (odpovídá severnímu pólu magnetu) a vstupují do opačného konce (jižního pólu).[10]
Díky tomu, že jsou magnetické indukční čáry uzavřené křivky, můžeme pro magnetické pole použít i označení pole vírové - neexistují totiž magnetické náboje, ze kterých by siločáry (tedy magnetické indukční čáry) začínaly a končily.[10]
Permanentní magnet
[editovat | editovat zdroj]Permanentní magnety mohou mít nejrůznější tvary. Silové účinky se projevují nejvíce na pólech magnetu (N a S). Rozpůlením tyčového magnetu vzniknou dva nové magnety s novými póly. Spojením více magnetů vznikne nový magnet se dvěma póly, přičemž silové účinky jednotlivých magnetů se sčítají. Magnetické indukční čáry vždy tvoří uzavřené křivky, procházející magnetem a vystupující u severního pólu do prostoru kolem magnetu, aby se do něj vrátily u jeho jižního pólu. Směr indukčních čar vyznačujeme vně magnetu od severního k jižnímu pólu (uvnitř magnetu od jižního k severnímu).[11]

Tyčový magnet
[editovat | editovat zdroj]Zobrazení indukčních magnetických čar tyčových magnetů pomocí železných pilin:



Přímý vodič
[editovat | editovat zdroj]Ve vodiči a v prostoru kolem vodiče protékaného proudem vzniká magnetické pole. Průchodem proudu vodičem vzniká magnetické pole, jehož magnetické indukční čáry mají tvar soustředných kružnic.[11]

Dlouhá cívka
[editovat | editovat zdroj]Magnetické pole v okolí cívky je tvořeno součtem magnetických polí jednotlivých závitů a podobá se magnetickému poli tyčového magnetu.[11]

Magnetické pole země
[editovat | editovat zdroj]Magnetické pole Země je indukované magnetické pole v určitém prostoru okolo Země. Značení pólů magnetů bylo odvozeno od pólů zeměkoule, která má také své magnetické pole (vytvářené otáčejícím se roztaveným železným jádrem Země).[11]
Historie
[editovat | editovat zdroj]
V přírodě lze nalézt určité látky, mezi kterými působí určité síly, které se označují jako magnetické síly. Tyto síly lze pozorovat i tehdy, když u nich nelze pozorovat žádný mikroskopický pohyb elektrických nábojů. Takové látky se označují jako magnetické látky. O tělesech, které vykazují magnetické vlastnosti, říkáme, že jsou zmagnetované, popř. je označujeme jako (permanentní) magnety. Tyto látky byly známy už ve starověku a bylo také známo působení (a existence) zemského magnetismu. Mnohé látky se mohou stát magnetickými vložením do magnetického pole – tento proces se označuje jako magnetizace.
Později bylo zjištěno, že podobné síly se objevují také v okolí vodiče, kterým protéká elektrický proud. Především na základě experimentů Ampèrových a Oerstedových pak byl zaveden pojem magnetického pole. Další výzkumy ukázaly úzkou vazbu mezi pohybem elektrického náboje a existencí magnetického pole.
Dalším krokem k pochopení magnetismu byla kompletní teorie elektromagnetického pole, která sjednocuje jevy elektrické a magnetické. Formuloval ji James Clerk Maxwell a je shrnuta v soustavě tzv. Maxwellových rovnic doplněných materiálovými vztahy. Z této teorie pak Albert Einstein vycházel při formulaci speciální teorie relativity. Ta chápe magnetické pole jako projev elektrického pole pohybujících se nabitých částic. S užitím relativistické kvantové teorie lze přibližně v tomto smyslu vysvětlit i pole permanentních magnetů.
Einstein v roce 1905 ukázal, že magnetické pole lze považovat za relativistickou část elektrického pole. Magnetické pole se totiž objevuje jako vedlejší produkt při Lorentzových transformacích souřadnic v přítomnosti elektrického pole. Lorentzovy transformace však nelze aplikovat na elektrické pole, pokud toto pole nepředpokládá existenci magnetického pole a jejich vzájemný vztah vyjádřený Maxwellovými rovnicemi (z tohoto hlediska lze tedy magnetické pole stěží považovat za vedlejší produkt elektrického pole). Pohybuje-li se elektrický náboj vzhledem k pozorovateli, pak elektrické pole v důsledku kontrakce délek a dilatace času není z hlediska pozorovatele sféricky symetrické. Jednou z částí Lorentzovy transformace je síla, působící pouze na pohybující se náboj. Právě tato část se označuje jako magnetické pole.
Poznámky
[editovat | editovat zdroj]- ↑ V tom se podobá elektrické indukci, popisující elektrické pole, jako by bylo vytvářeno pouze volnými náboji. Z historických důvodů jsou však názvy intenzita a indukce u elektrického a magnetického pole vzhledem k fyzikální podstatě opačné, umožňují však mnohé analogie ve vztazích pro lineární prostředí, využívané v technické praxi.
Reference
[editovat | editovat zdroj]- ↑ a b ČSN ISO 31-5 Veličiny a jednotky: Elektřina a magnetismus, Český normalizační institut, Praha 1994
- ↑ BREDOV, M. M.; RUMJANCEV, V. V.; TOPTYGIN, I. N. Klassičeskaja elektrodinamika. 1. vyd. Moskva: Nauka, 1985. 400 s. Část II, hlava I., § 2.2, s. 200–201. (rusky)
- ↑ SEDLÁK, Bedřich; ŠTOLL, Ivan. Elektřina a magnetismus. 1. vyd. Praha: Academia a Karolinum, 1993. 600 s. ISBN 80-200-0172-7. Kapitola 3.5.6, s. 236.
- ↑ HORÁK, Zdeněk; KRUPKA, František. Fyzika. Příručka pro vysoké školy technického směru. 3. vyd. Praha: SNTL/ALFA, 1981. 04-017-81. Kapitola 6.10.3, 6.11.7, s. 635, 657–9.
- ↑ ČSN EN 80000-6 Veličiny a jednotky - Část 6: Elektromagnetismus. Úřad pro technickou normalizaci, metrologii a státní zkušebnictví, Praha, leden 2009.
- ↑ ČSN ISO 31-5 Veličiny a jednotky. Část 5: Elektřina magnetismus. Položka 5-22.1. Český normalizační institut, 1995.
- ↑ Indukované elektrické napětí, eluc.kr-olomoucky.cz, ELUC.
- ↑ http://www.osel.cz/index.php?clanek=7436 - Přelomové pozorování magnetických monopólů ve kvantovém oblaku
- ↑ WPJ.CZ. Magnetické otazníky 17 – Co jsou indukční čáry, bipolární magnet a magnetická guma? | Unimagnet - Unimagnet.cz. www.unimagnet.cz [online]. [cit. 2021-11-23]. Dostupné online.
- ↑ a b c Magnetické pole – WikiSkripta. www.wikiskripta.eu [online]. [cit. 2021-11-23]. Dostupné online.
- ↑ a b c d Střední škola automobilní. www.skola-auto.cz [online]. [cit. 2021-11-23]. Dostupné online.
Související články
[editovat | editovat zdroj]- Magnetický moment
- Magnetizace (veličina)
- Magnetické pole planet
- Geomagnetické pole
- Elektromagnetické pole
- Elektrické pole
- Toroid
Externí odkazy
[editovat | editovat zdroj] Obrázky, zvuky či videa k tématu magnetické pole na Wikimedia Commons
Obrázky, zvuky či videa k tématu magnetické pole na Wikimedia Commons - P.B.Price, Evidence for detection of moving magnetic monopole
- B. Cabrera, First Results from a Superconductive Detector for Moving Magnetic Monopoles
- A. Caplin, Observation of an unexplained event from a magnetic monopole detector































































































