Logaritmus
Logaritmus kladného reálného čísla při základu () je takové reálné číslo
- , pro které platí .
V tomto vztahu se číslo a označuje jako základ logaritmu (báze), logaritmované číslo x se někdy označuje jako argument či numerus, y je pak logaritmem čísla x při základu a. Pro každé kladné číslo a kladný základ různý od jedné existuje právě jeden logaritmus, což je důsledkem vlastností exponenciální funkce-monotonie, spojitosti a oboru hodnot . Logaritmická funkce je funkce, která je inverzní k exponenciální funkci. Zvláštní význam mají logaritmy o základu 10 (dekadický logaritmus, zkráceně log nebo lg) a o základu e (Eulerovo číslo, přirozený logaritmus, zkráceně ln).

Původ
[editovat | editovat zdroj]Označení logaritmus pochází ze staré řečtiny, λόγος je zákon a ἀριθμός číslo.
Počátkem novověku, s rozvojem astronomie a geodézie a s potřebami námořní navigace, nesmírně vzrostla potřeba složitých výpočtů, zejména trigonometrických, a to na velký počet platných číslic. O myšlence nahradit násobení sčítáním se poprvé zmiňuje korespondence švýcarského matematika a hodináře Josta Bürgiho v roce 1588. Ten skutečně sestavil tabulky funkce sinus a brzy po roce 1600 i tabulky jejích logaritmů, které však publikoval až roku 1620 v Praze. O šest let dříve publikoval metodu logaritmů skotský matematik John Napier, který tak platí za jejich objevitele, a roku 1617 publikoval první tabulky desítkových ("briggsových") logaritmů Angličan Henry Briggs.
Logaritmy se tak staly základem pro ekonomické výpočty (úlohy na úročení, složené úročení, inflaci). Do 2. poloviny 20. století se proto používaly logaritmická pravítka a logaritmické tabulky, které byly nezbytnou pomůckou inženýrů, ekonomů, astronomů, geodetů, ale i námořních kapitánů a studentů, protože umožňovaly nahradit násobení a dělení prostým sčítáním a odčítáním. Každý středoškolák se učil zacházet se školními, pěti- nebo sedmimístnými tabulkami (k dispozici byly i tabulky s přesností na 10 a 14 platných číslic). Pro přibližné technické výpočty (na 3-4 platná místa) se od poloviny 19. století rozšířilo logaritmické pravítko, jehož používání bylo vyučováno ve školách. Teprve s příchodem sálových počítačů v 60. letech 20. století, kalkulaček v 80. letech 20. století a tabulkových procesorů na osobních počítačích v 90. letech 20. století vymizela potřeba usnadňovat (ruční) výpočty pomocí logaritmů (tabulky, logaritmické pravítko).
Intuitivní odvození
[editovat | editovat zdroj]Myšlenka logaritmu vznikla jako rozšíření myšlenky exponentu. Že 2 × 2 = 4 můžeme zapsat také jako 21 × 21 = 22 a místo 4 × 8 = 32 můžeme napsat 22 × 23 = 25. Exponent součinu je tedy součet exponentů obou součinitelů, takže při zvoleném základu (2) můžeme násobení převést na sčítání exponentů, zatím jen pro celé exponenty. Podobně můžeme zapsat i dělení: 32:4 = 25: 22 = 23, čili 8. Stejně 1/2 = 1:2 = 20:21 = 2−1 čili 0,5. Místo dělení stačí odečítat exponenty.
Číslo 2 jsme zvolili jako základ a místo „exponentu dvou“ můžeme psát log2. Můžeme tedy napsat, že log2 32 = 5, log2 8 = 3, log2 4 = 2, log2 1 = 0 a log2 0,5 = −1. Pro každé číslo x (kromě nuly) platí, že log2 2x = (log2 x) + 1, log2 4x = (log2 x) + 2. Protože 8 = 23, můžeme také psát 8 = 21 × 21 × 21 = 2(1+1+1) a 8 = 2(3x1), takže místo umocňování stačí exponent násobit a místo odmocnění exponent dělit.
Kdybychom místo dvojky zvolili základ 10 (desítkový logaritmus), můžeme psát log10 0,1 = −1, log10 1 = 0 (to platí pro každý základ), log10 100 = 2 atd. I tady bude platit, že log1010x = (log10 x) + 1, log10 100x = (log10 x) + 2.
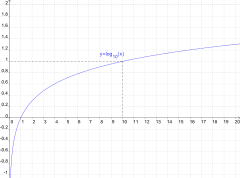
Dokud jsme mluvili o exponentech, mělo to smysl jen pro celá čísla. Když jsme ale zmínili, že místo odmocňování stačí exponent dělit, může vyjít i necelé číslo: druhou odmocninu z deseti bychom mohli zapsat jako 10(0,5). To je právě to, co dělá logaritmická funkce: pokud různé hodnoty výrazu zx vyneseme do grafu (viz obrázek), můžeme jimi proložit spojitou křivku – logaritmickou funkci, která má hodnotu pro všechna reálná x>0. Logaritmus čísla 3 bude někde mezi log101 a log1010, tedy reálné číslo někde mezi nulou a jedničkou. Z logaritmické tabulky můžeme zjistit, že log10 3 = 0,47712125472, takže číslo 3 můžeme zapsat jako 100,47712125472. I zde bude platit, že log10 10x = (log10 x) + 1, log10 0,1x = ( log10 x) - 1, že logaritmus součinu se rovná součtu logaritmů obou činitelů a logaritmus podílu se rovná rozdílu logaritmus dělence minus logaritmus dělitele. Logaritmus mocniny je násobek exponentu a logaritmu mocněnce. Logaritmus odmocniny je podíl logaritmu odmocněnce a odmocnitele.
Vlastnosti logaritmů
[editovat | editovat zdroj]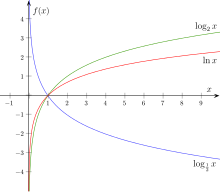
- (Logaritmus je inverzní funkcí k exponenciální funkci o stejném základu. Speciálně: )
- (Logaritmus součinu je součet logaritmů jednotlivých činitelů.)
- (Logaritmus podílu je rozdíl logaritmů čitatele a jmenovatele.)
- (tzn. ; logaritmus mocniny je roven exponent krát logaritmus základu.)
- (Formule umožňující vyčíslit logaritmus libovolného základu pomocí kalkulačky, případně logaritmických tabulek.)
Vlastnosti logaritmických funkcí
[editovat | editovat zdroj]Pro každou logaritmickou funkci platí:
- je monotónní, spojitá a má derivace všech řádů;
- pro a > 1 je rostoucí a ryze konkávní, pro a ∈ (0; 1) je klesající a ryze konvexní;
- (graf funkce prochází bodem [1;0]);
- osa y je asymptotou grafu.
Funkcionální rovnice
[editovat | editovat zdroj]Logaritmické funkce jsou právě ta spojitá (a nenulová) řešení funkcionální rovnice , která je tedy definuje.
Tato vlastnost byla základem použití logaritmů pro zjednodušení numerických výpočtů a vyjadřuje izomorfismus aditivní grupy reálných čísel a multiplikativní grupy kladných reálných čísel.
Logaritmus komplexního čísla
[editovat | editovat zdroj]Často je potřeba vypočítat přirozený logaritmus komplexního čísla. Platí:
Byl zde použit exponenciální tvar komplexního čísla. Proměnná udává absolutní hodnotu hodnotu komplexního čísla a udává argument (polární úhel goniometrického tvaru) komplexního čísla.
Máme-li tedy komplexní číslo, pak reálná část jeho logaritmu je rovna logaritmu absolutní hodnoty, zatímco imaginární udává argument. Je nutno uvést, že argument komplexního čísla není definován jednoznačně, může se lišit o celé násobky . Proto se někdy zavádí tzv. hlavní hodnota logaritmu , u které se většinou uvažují úhly z intervalu .
Pokud z definičního oboru odstraníme nekladnou reálnou poloosu, tak je logaritmus holomorfní funkce s derivací rovnou .
Využití
[editovat | editovat zdroj]Logaritmus je inverzní funkce k exponenciální funkci.
Neznámá v exponentu mocniny
[editovat | editovat zdroj]Logaritmování umožňuje najít neznámý exponent mocniny u úloh využívajících exponenciální funkci (např. složené úročení, radiokarbonová metoda datování) a řešit takové rovnice.
Příklad řešení rovnice
- obě strany rovnice můžeme zlogaritmovat:
- využijeme pravidlo pro práci s logaritmy:
- vyčíslíme výsledek:
Desítková soustava a logaritmus
[editovat | editovat zdroj]Kolik číslic bude mít mocnina daného čísla. Protože je naše číselná soustava desítková, vypočteme dekadický logaritmus zadané mocniny (z výsledku vyplývá, že číslo má celkem 31 cifer):
Zjednodušení výpočtů
[editovat | editovat zdroj]Pomocí výše uvedených rovností lze složitější operace převádět na jednodušší (násobení a dělení na sčítání a odčítání, mocnění a odmocniny na násobení a dělení), což se zvláště před rozšířením elektronických kalkulaček a počítačů využívalo při složitějších výpočtech prováděných ručně nebo mechanickými kalkulátory (které obvykle uměly jen sčítat). Pro usnadnění přepočtů existovaly logaritmické tabulky s předem vypočítanými hodnotami logaritmů, případně logaritmické pravítko, mechanická pomůcka pro výpočty pomocí logaritmů. Dnes patří tyto postupy do historie, ale jsou dobré cvičení pro pochopení toho, jak logaritmy fungují.
Příkladem využití logaritmů je výpočet pomocí logaritmických tabulek:
- Nejprve se výraz zlogaritmuje:
- Logaritmovaná čísla se upraví na semilogaritmický tvar (abychom hledali jen logaritmy čísel mezi 1 a 10, obsažené v tabulkách): atd.
- V tabulkách se vyhledají příslušné logaritmy (tabulky ovšem obsahují hodnoty jen na několik platných číslic):
- log 17300 ≅ 4,2380
- log 15478 ≅ 4,1897
- Vypočte se výsledný logaritmus: log x = 4,2380 + 2,0949 = 6,3329 = 6 + 0,3329
- Výsledek se odlogaritmuje, v tabulkách najdeme, že 0,3329 je log 2,1522, takže .
- Přesnější výsledek spočtený na běžné kalkulačce je 2 152 303, tzn. relativní chyba výsledku je asi 0,005 %).
Logaritmické pravítko
[editovat | editovat zdroj]Pro složitější výpočty bylo dříve místo kalkulaček používáno logaritmické pravítko (zhruba do 70. let 20. století), kde byla stupnice logaritmická, a tak bylo možné dvěma posuvnými stupnicemi snadno zjistit výsledek násobení (nahrazení součinu součtem). Logaritmické pravítko bylo tehdy používáno pro technické výpočty (např. v Programu Apollo pro první lety na Měsíc), pro geodetické výpočty, atd.
Logaritmická stupnice grafu
[editovat | editovat zdroj]Logaritmická stupnice je používána v grafech pro zdůraznění malých hodnot a zároveň potlačení příliš velkých hodnot. Graf poté také ukazuje procentuální změny (místo absolutní změny).
Odlišení mocninné a exponenciální funkce
[editovat | editovat zdroj]Pokud použijeme na svislou osu y logaritmické měřítko, lze jedním pohledem zjistit, zda zobrazená křivka představuje mocninnou nebo exponenciální funkci. Pokud se po zlogaritmování svislé osy stane z křivky přímka, šlo o exponenciální funkci. Bude-li nutné pro dosažení přímky zlogaritmovat i vodorovnou osu x, jde o mocninnou funkci. Z nutného postupu pro logaritmickou transformaci obou os (x a y) pro dosažení přímky lze odvodit předpis pro zobrazenou funkci.
Koncentrace roztoků
[editovat | editovat zdroj]Některé veličiny nabývají výrazného rozpětí hodnot, až několika řádů. Příkladem může být koncentrace kationtů H3O+ v roztoku:
| roztok | Kyselina octová | Pivo | Mléko | Mořská voda | Amoniak |
|---|---|---|---|---|---|
| koncentrace H3O+ | 0,0013 | 0,00003 | 0,0000003 | 0,00000001 | 0,000000000003 |
Je zřejmé, že při zobrazení těchto hodnot na číselné ose bude pivo přibližně 43× blíže k nule než ocet (0,0013/0,00003), mléko bude 100× blíže k nule než pivo (0,00003/0,0000003) a ostatní hodnoty také budou „namačkány“ v těsné blízkosti nuly. Přestože například koncentrace H3O+ v mléku je stále 100000× (o pět dekadických řádů) vyšší než ve čpavku.
V takovém případě je výhodnější místo samotné koncentrace zobrazovat její logaritmus, tedy volně řečeno „řád koncentrace“. Tabulka po zlogaritmování bude vypadat následovně.
| roztok | Kyselina octová | Pivo | Mléko | Mořská voda | Amoniak |
|---|---|---|---|---|---|
| log10(koncentrace H3O+) | −2,9 | −4,5 | −6,5 | −8 | −11,5 |
Je vidět, že takto upravené hodnoty jsou celkem rozumně rozloženy mezi −11,5 a nulou. Na závěr dodejme, že pH je definováno přibližně takto, pouze logaritmus koncentrace je uváděn bez znaménka. (Koncentrace je vždy menší nebo rovna 1, proto logaritmus koncentrace bude vždy menší nebo roven 0.)
Další využití logaritmů
[editovat | editovat zdroj]Logaritmy se objevují také v mnoha vědeckých oborech pro vyjádření závislosti na exponentu. Příkladem jsou jednotky decibel a neper, v chemii vyjadřování kyselosti roztoků pomocí pH a další. V případě lidského vnímání jde o aplikaci Weberova–Fechnerova zákona, který popisuje závislost lidské odezvy na fyzikální stimuly, tedy mění-li se fyzikální podněty působící na naše smysly řadou geometrickou, vnímáme jejich změnu řadou aritmetickou.
Hvězdná velikost
[editovat | editovat zdroj]Při vyjadřování hvězdné velikosti (magnitudo) je využívána logaritmická stupnice, která umožňuje zachovat subjektivně stanovené třídy jasnosti hvězd, jak je ve starověku definoval Hipparchos (2. století př. n. l.).
Zemětřesení
[editovat | editovat zdroj]Logaritmickou stupnici používají jednotky magnitudo pro měření míry zemětřesení (Richterova stupnice).
Speciální základy
[editovat | editovat zdroj]Desítkový logaritmus
[editovat | editovat zdroj]U logaritmu o základu 10 (nazývaného desítkový či dekadický logaritmus, příp. Briggsův podle Henryho Briggse) se ve značení vynechává základ a píše se jen prostě log x, někdy se používá také speciální značení lg x. Je třeba si však dát pozor: použité značení se může v různých odborných literaturách lišit. lg x se běžně využívá ve významu a ne .
Přirozený logaritmus
[editovat | editovat zdroj]Logaritmus o základu e () se označuje jako přirozený logaritmus (někdy také Napierův podle Johna Napiera) a značí se (logaritmus naturalis, latinsky přirozený logaritmus). Vznikl tak, že se hledal základ exponenciální funkce tak, aby tečnou této exponenciály v bodě A=(0,1) byla přímka . Odpovídající základ byl označen písmenem e a pojmenován Eulerovo číslo (podle Leonharda Eulera, který se podílel na objevu tohoto čísla).
Přirozený logaritmus - pravidlo výchozího stavu a změny (změna nemůže být menší než nula - logaritmus 1 je nula, z čehož plyne přirozený logaritmus o základně Eulerovy konstanty vymezuje právě takový průběh funkce (přesněji inverzní exponenciální funkce - obecně nazývané jako funkce logaritmická), kdy nemůže dojít k nižší hodnotě než výchozí stav.
Exponent této funkce při znázornění v kartézských souřadnicí je vlastně tečnou této funkce přirozeného logaritmu na základě Eulerovy konstanty - a tato tečna je vlastně další funkcí - funkcí nižšího řádu která již není exponenciální.
V rovnici by zápis tečny funkce přirozeného logaritmu (a současně exponent přirozeného logaritmu)
y = x + 1 (což je vlastně další, již neexponenciální funkce),
zatímco výchozí funkce pro přirozený logaritmus by měla v rovnici znít
y = e (exponent/argument x + 1).
Binární logaritmus
[editovat | editovat zdroj]Hlavně v informatice se objevuje logaritmus o základu dva (binární logaritmus), který je v příslušném kontextu někdy značen , případně .
Platí:
Např. při binárním vyhledávání v setříděném seznamu, který má n položek, je potřeba maximálně kroků k nalezení hledané hodnoty. Tato technika je totiž založena na půlení intervalů.
Iracionalita
[editovat | editovat zdroj]Dekadický logaritmus je racionální číslo právě pro racionální mocniny čísla 10, např.
Desítkové logaritmy přirozených čísel kromě mocnin 10, např.
jsou iracionální čísla, což je důsledkem základní věty aritmetiky.
Přirozené logaritmy všech přirozených čísel kromě 0 a 1, např.
jsou vesměs iracionální, což plyne z transcendence čísla e.
Taylorova řada pro logaritmus
[editovat | editovat zdroj]Pomocí vztahu pro Taylorův rozvoj, případně zintegrováním geometrické řady
(člen po členu) lze obdržet (Maclaurinův) rozvoj logaritmu do řady kolem bodu 1:
Tato řada má poloměr konvergence 1, navíc konverguje i pro krajní bod , kde obdržíme známou Leibnizovu řadu pro (konverguje však velmi pomalu):
Řadu pro logaritmus je možné vyčíslit i pro ryze imaginární číslo . Pak z předchozího vyplývá, že platí:
Stejně tak lze tento výraz vyjádřit pomocí řady:
Porovnáním imaginárních částí vznikne řada pro :
Dosazením vyjde řada pro Ludolfovo číslo:
Tato řada však bohužel také konverguje velmi pomalu.
Odkazy
[editovat | editovat zdroj]Související články
[editovat | editovat zdroj]Externí odkazy
[editovat | editovat zdroj] Obrázky, zvuky či videa k tématu logaritmus na Wikimedia Commons
Obrázky, zvuky či videa k tématu logaritmus na Wikimedia Commons  Slovníkové heslo logaritmus ve Wikislovníku
Slovníkové heslo logaritmus ve Wikislovníku- Logaritmus v encyklopedii MathWorld (anglicky)
- Logaritmické tabulky čísel od 1 000 000 do 9 999 999














![{\displaystyle \log _{b}{\sqrt[{n}]{a}}={\frac {1}{n}}\log _{b}a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f4535306976bd41cef42e5575a9a175f552c7a0)
















































