Exponenciální funkce

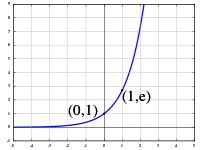
Exponenciální funkce je matematická funkce ve tvaru , kde je kladná reálná konstanta různá od , která je nazývána základ. Exponent je reálná nezávisle proměnná (argument), definici lze ovšem rozšířit na komplexní argumenty i na složitější objekty, zejména lineární operátory. Inverzní funkcí k exponenciální funkci je funkce logaritmus Křivku, která je grafem exponenciální funkce, nazýváme exponenciála a často je tak nazývána i sama exponenciální funkce.
Exponenciální funkce neustále zrychluje svůj růst, má tzv. exponenciální růst, což je běžně používaný pojem. Je však používán i pojem exponenciální pokles. V přírodě se exponenciální růst vyskytuje například u šíření virů (např. nástup epidemie chřipky, exponenciální pokles pak při jejím ústupu) nebo dělení buněk v ideálním prostředí (růst však není nekonečný, ale narazí dříve či později na limity prostředí). V ekonomii je exponenciální růst u složeného úročení nebo žádoucí průběh ukazatele, který například odpovídá zvyšování odbytu nově uváděného zboží na trh.
Charakteristika[editovat | editovat zdroj]
V oboru reálných čísel je exponenciální funkce pro (ostře) rostoucí, pro (ostře) klesající.
Pro exponenciální funkci platí exponenciální identita:
- ,
díky které je možné definovat hodnoty exponenciální funkce i pro jiné než celočíselné argumenty (viz část Definice článku Umocňování).
Derivací exponenciální funkce je opět exponenciální funkce vynásobená přirozeným logaritmem základu:
- .
Významnou roli má exponenciální funkce s takovým základem, že je přesně rovna své derivaci. Tímto základem je Eulerovo číslo a tuto funkci nazýváme přirozená exponenciální funkce. Zapisujeme ji také jako exp x, což umožňuje zápis v jednom řádku bez exponentů:
- .
Důležitou exponenciální funkcí je také dekadická exponenciální funkce, která má základ rovný deseti, tedy .[1]
Exponenciální funkci s obecným základem lze převést na základ pomocí vzorce .
Formální definice[editovat | editovat zdroj]

Exponenciální funkce ex může být charakterizována různými ekvivalentními způsoby. Zejména může být definována následující mocninnou řadou:
Méně často je ex definováno jako řešení y rovnice
- .
Lze ji definovat také následující limitou:
- .
Vlastnosti exponenciální funkce reálného argumentu[editovat | editovat zdroj]
V oboru reálných čísel pro každou exponenciální funkci () platí:
- je zdola omezená
- je prostá
- je spojitá v každém bodě, ale není stejnoměrně spojitá na celém
- pro a > 1 je rostoucí, pro a ∈ (0; 1) klesající
- (tedy graf exponenciální funkce prochází bodem [0;1])
- ve speciálním případě .
Exponenciála o základu e[editovat | editovat zdroj]
Často používaný základ exponenciální funkce je Eulerovo číslo , kdy ji nazýváme přirozená exponenciální funkce.
Funkce je až na násobek jediné řešení diferenciální rovnice
Funkce se obvykle definuje mocninnou řadou
která konverguje pro každé reálné i komplexní . Obecná exponenciální funkce se pak dá definovat jako
kde je přirozený logaritmus čísla .
Dosazením čistě imaginárního čísla do definice exponenciály dostáváme vztah .
Derivace a diferenciální rovnice[editovat | editovat zdroj]
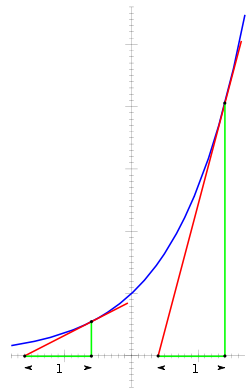
Důležitost exponenciální funkce v matematice a přírodních vědách pramení hlavně z vlastností její derivace, zejména:
Důkaz:
To znamená, že ex je svou vlastní derivací a tedy je jednoduchým příkladem pfaffovské funkce. Funkce tvaru cex (kde c je konstanta) jsou jediné funkce s touto vlastností (podle Picardovy–Lindelöfovy věty).
Tato vlastnost se dá vyjádřit i následujícími způsoby:
- Sklon grafu v libovolném bodě je hodnota funkce v tomto bodě.
- Tempo růstu funkce x je stejné jako hodnota funkce v bodě x.
- Funkce řeší diferenciální rovnici y′ = y.
- exp je pevný bod derivace.
Krom toho u diferencovatelné funkce f(x) používáme řetízkové pravidlo:
Vztah logaritmické a exponenciální funkce[editovat | editovat zdroj]
Exponenciální a logaritmická funkce jsou navzájem inverzní, tedy platí:
- , .
Grafy těchto funkcí jsou osově souměrné podle přímky .
Řetězové zlomky pro exponenciální funkci[editovat | editovat zdroj]
Řetězový zlomek pro ex lze získat prostřednictvím Eulerovy rovnosti:
Následující celkový řetězový zlomek pro ez konverguje mnohem rychleji:
nebo použitím substituce :
zvláštní případ pro z = 2:
Tento vzorec také konverguje, ale pomaleji, protože z > 2. Například:
Exponenciála operátorů[editovat | editovat zdroj]
Mocninná řada v definici exponenciály umožňuje definovat exponenciálu i mnohem komplikovanějších objektů, než jsou komplexní čísla, zejména matic a operátorů. Mocniny a součty operátorů, respektive matic, jsou dobře definované a příslušná řada konverguje.
Komplexní rovina[editovat | editovat zdroj]

Stejně jako v reálném případě, exponenciální funkce může být definována na komplexní rovině několika ekvivalentními formami. Jedna taková definice je ekvivalentní definicí mocninnou řadou, kde je reálná proměnná nahrazena komplexní:
Exponenciální funkce je periodická s imaginární periodou 2πi a může být psána jako
- ,
kde a a b jsou reálné hodnoty a kde na pravé straně se vyskytují reálné funkce, pokud je tento předpis použit jako definice (Eulerův vzorec). Tento vzorec propojuje exponenciální funkci s goniometrickými a hyperbolickými funkcemi.
Uvažujeme-li funkci definovanou na komplexní rovině, pak exponenciální funkce zachovává tyto vlastnosti:
pro všechny z a w.
Exponenciální funkce je celá funkce neboť je holomorfní na celé komplexní rovině. Každé komplexní číslo kromě 0 má při exponenciální funkci svůj vzor; to znamená, že 0 je lacunární hodnota exponenciální funkce. Ilustruje tedy malou Picardovu větu, že jakákoli nekonstantní celá funkce má ve svém obrazu až na jeden bod celou komplexní rovinu.
Rozšířením přirozeného logaritmu do komplexních čísel získáme komplexní logaritmus log z, což je vícehodnotová funkce.
Pak můžeme definovat obecnou mocninu:
pro všechna komplexní čísla z a w. To je také vícehodnotová funkce, a to i když z je reálné. Tento fakt je poněkud problematický, neboť vícehodnotové funkce log z a zw lze lehce zaměnit s jejich jednohodnotovými ekvivalenty dosazením reálného čísla za z. Pravidlo o násobení exponentů v případě pozitivních reálných čísel musí být upraveno pro vícehodnotový kontext:
- (ez) w
≠ ezw, ale spíše (ez) w
= e(z + 2πin)w vícehodnotový po celých číslech n.
Exponenciální funkce zobrazuje každou přímku v komplexní rovině na logaritmické spirály v komplexní rovině se středem v počátku. Existují dva zvláštní případy: když původní přímka je rovnoběžná s reálnou osou, výsledná spirála se nikdy neuzavírá do sebe; a když původní přímka je rovnoběžná s imaginární osou, výsledná spirála je kruh o nějakém poloměru.
- Exponenciální funkce na komplexní rovině
-
z = Re(ex + iy)
-
z = Im(ex + iy)
Odkazy[editovat | editovat zdroj]
Reference[editovat | editovat zdroj]
- ↑ HAVRLANT, Lukáš. Exponenciální funkce. Matematika po lopatě.
Související články[editovat | editovat zdroj]
Externí odkazy[editovat | editovat zdroj]
 Obrázky, zvuky či videa k tématu exponenciální funkce na Wikimedia Commons
Obrázky, zvuky či videa k tématu exponenciální funkce na Wikimedia Commons




















































