Pythagorova věta

Pythagorova věta: Součet obsahů čtverců nad odvěsnami (modrá plus červená plocha) se rovná obsahu čtverce nad přeponou pravoúhlého rovinného trojúhelníku (fialová plocha)

Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlých trojúhelníků v euklidovské rovině. Umožňuje dopočítat délku třetí strany takového trojúhelníku, pokud jsou známy délky dvou zbývajících stran.

Věta zní:

Obsah čtverce sestrojeného nad přeponou libovolného pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami (dvěma kratšími stranami).

Formálně Pythagorovu větu vyjadřuje rovnice

$c^{2}=a^{2}+b^{2}$,

kde $c$ označuje délku přepony pravoúhlého trojúhelníku a délky odvěsen jsou označeny $a$ a $b$.

Pythagorova věta v byzantském matematickém rukopisu (13./14. století), Vatikánská apoštolská knihovna

Historie

Věta byla pojmenována podle řeckého filosofa a matematika Pythagora, jenž ji v 6. století př. n. l. objevil pro Evropu, resp. starověkou Indii. Pravděpodobně však byla známa i v jiných starověkých civilizacích dávno předtím (v Babylonii, v Číně, v Egyptě).

Příklad použití

Obdélníkové náměstí má délky stran 30 a 40 metrů. Kolik metrů bude měřit cesta, která povede po úhlopříčce náměstí rovně z jednoho rohu do druhého?

Řešení: Představme si jeden ze dvou trojúhelníků, na něž cesta náměstí rozdělí.

Součet čtverců délek jeho odvěsen (stran náměstí) je 30² m² + 40² m² = 900 m² + 1600 m² = 2500 m².

Toto číslo se podle Pythagorovy věty zároveň rovná čtverci přepony trojúhelníku. Stačí je tedy odmocnit, a dostaneme délku přepony. Odmocnina z 2500 m² je 50 m, a to je hledaná délka úhlopříčné cesty.

Zobecnění Pythagorovy věty

Nahrazení čtverců jinými plošnými obrazci

Součet obsahů podobných obrazců nad odvěsnami se rovná obsahu jim podobného obrazce nad přeponou pravoúhlého rovinného trojúhelníku (zde pravidelné pětiúhelníky).

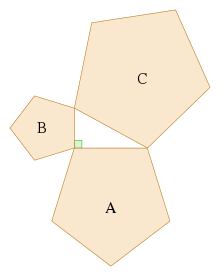
Čtverce lze ve formulaci věty zaměnit jakýmikoliv jinými obrazci (kružnicí, obdélníkem, trojúhelníkem, pětiúhelníkem) za předpokladu, že jsou si navzájem podobné a jejich rozměry jsou úměrné délce příslušné strany trojúhelníku. Součet obsahů těchto obrazců nad odvěsnami bude opět shodný s obsahem obrazce nad přeponou.

Vyplývá to z formulace původní věty se čtverci nad stranami trojúhelníku, protože obsah každého z obrazců je díky platnosti předpokladů úměrný obsahu čtverce nad danou stranou a konstanta úměrnosti $k$ je vždy táž díky vzájemné podobnosti obrazců i čtverců.

Zobecnění na tři obecné vektory v Hilbertově prostoru

Pythagorovu větu lze zobecnit na jakýkoliv vektorový prostor se skalárním součinem (Hilbertův prostor). Trojúhelníkem v tomto případě myslíme tři vektory a, b, c takové, že c = b - a a že a a b jsou na sebe kolmé. Pak platí podobný vztah mezi normami těchto vektorů, jako v případě rovinného trojúhelníku:

$\|\mathbf {a} \|^{2}+\|\mathbf {b} \|^{2}=\|\mathbf {c} \|^{2}$,

kde $\|\cdot \|$ značí normu na daném vektorovém prostoru.

Z této obecnější formulace lze odvodit i původní rovinnou verzi věty. Pokud rovinu chápeme jako 2-rozměrný Euklidův prostor s obyčejným skalárním součinem a v trojúhelníku ABC s pravým úhlem u vrcholu C označíme a = B - C, b = A - C a c = A - B (= b - a), plyne původní Pythagorova formulace ze vztahu norem vektorů, uvědomíme-li si, že v tomto případě je norma vektoru pouze délka odpovídající strany.

Zobecnění na více dimenzí

Větu lze zobecnit i na více než dvě dimenze. Například pokud umocníme délku tělesové úhlopříčky kvádru (např. cihly) na druhou, bude se toto číslo rovnat součtu čtverců délek všech tří rozměrů kvádru. Analogické vztahy platí i v euklidovských prostorech vyšších rozměrů.

Matematicky řečeno, je zde čtverec délky (normy) vektoru roven součtu čtverců jeho souřadnic v libovolné ortonormální bázi. Tuto představu lze zobecnit i na prostory nekonečné dimenze.

Kosinová věta – zobecnění na jiné než pravé úhly

Není-li úhel mezi stranami $a$ a $b$ pravý, je třeba jeho velikost γ zavést do vztahu v rámci dalšího sčítance:

$c^{2}=a^{2}+b^{2}-2ab\cos \gamma$,

což je formulace kosinové věty. Důkaz kosinové věty lze podat rozdělením trojúhelníku na dva pravoúhlé.

Důkazy Pythagorovy věty

Důkazů Pythagorovy věty existuje velmi mnoho (uvádí se, že až 300). Zde je několik z nich.

Důkaz č. 1

Pythagorova věta

Jedná se o grafický důkaz. Čtverec o straně $a+b$ lze složit dvěma způsoby (viz obrázek):

• ze 4 pravoúhlých trojúhelníků o délkách stran $a$, $b$, $c$ a dvou čtverců o délkách stran $a$ a $b$
• ze 4 pravoúhlých trojúhelníků o délkách stran $a$, $b$, $c$ a jednoho čtverce o straně c

Z rovnosti obsahu čtverce při obou způsobech složení pak plyne i Pythagorova věta.

Důkaz č. 2

Jde jen o zápis Důkazu č. 1 pomocí rovnic. Obsah celého čtverce lze vyjádřit dvěma způsoby (jen pravá část obrázku):

• Strana čtverce je složena ze stran trojúhelníku $a$ i $b$. Pro obsah tedy platí: $S=(a+b)\cdot (a+b)=(a+b)^{2}=a^{2}+2ab+b^{2}$

• Čtverec je tvořen 4 barevnými pravoúhlými trojúhelníky a bílým čtvercem se stranou $c$ uprostřed. Obsah celého čtverce je tedy součtem obsahu 4 pravoúhlých trojúhelníků ($4ab/2=2ab$) a bílého čtverce uprostřed se stranou $c$ ($c\cdot c=c^{2}$), tedy $\ S=2ab+c^{2}$

Protože se jedná o tentýž velký čtverec, musí se jeho obsah spočtený oběma způsoby rovnat, a tedy $\ a^{2}+2ab+b^{2}=2ab+c^{2}$, z čehož dostáváme tvrzení $\ a^{2}+b^{2}=c^{2}$.

Důkaz č. 3

Důkaz č. 3: podobnost trojúhelníků

Lze se snadno přesvědčit, že pokud jsou zeleně vyznačené úhly (úhel DCB a úhel DAC, který se rovná BAC) v obrázku vpravo shodné, jsou si trojúhelníky ABC, CBD a ACD navzájem podobné (velikosti jejich stran jsou ve stejném poměru, jejich úhly jsou stejně velké).

Grafická ilustrace rovnosti úhlů

→

Dílčí trojúhelníky, které vznikly rozdělením pravoúhlého trojúhelníku jeho výškou, je možno přeskupit a položit přes sebe. Protože všechny tři trojúhelníky mají stejné úhly a liší se jen velikostí, označujeme je za sobě podobné.

Z podobnosti dále vyplývá, že poměry jejich stran musejí být shodné. Z tohoto faktu vyšel i Pythagoras. Výpočet na sousedním obrázku ukazuje, jak jednoduchou úpravou dostáváme Pythagorovu větu.

Pythagorovu větu lze také dokázat pomocí kosinové věty, jelikož je Pythagorova věta jejím speciálním případem. Pokud tedy platí věta kosinová, platí i věta Pythagorova.

Algebraický důkaz podobnosti trojúhelníků

Součet úhlů trojúhelníku musí být 180°. Když je v každém z těchto tří trojúhelníků jeden úhel pravý (má 90°), tak to znamená, že i součet zbývajících dvou úhlů musí být 90°. V dílčích trojúhelnících známe vždy dva úhly, proto lze dopočítat i třetí.

Platí tedy:

1. BAC + ACB(90°) + CBA(CBD) = 180°
2. CBD + BDC(90°) + DCB = 180°
3. DAC + ACD + CDA(90°) = 180°

Z toho vyplývá, že:

1. BAC(DAC) + CBA(CBD) = 90°
2. CBD + DCB = 90°
3. DAC(BAC) + ACD = 90°

Z 1. a 3. rovnice vyplývá (BAC a DAC jsou si rovny!), že CBA(CBD) = ACD.

Pokud CBA (stejný jako CBD) dosadíme do 3. rovnice místo ACD, ze srovnání s 2. rovnicí

2. CBD + DCB = 90°

3. DAC + CBA (ACD, CBD) = 90°

pak vyplývá, že:

DCB = DAC

Trojúhelníky si jsou tedy podobné.

Důkaz č. 4

Popis stran v trojúhelníku pro důkaz pomocí Eukleidových vět

Tento důkaz využívá Eukleidových vět o odvěsnách:

$a^{2}=c\cdot c_{a}$

$b^{2}=c\cdot c_{b}$

Rovnice sečteme:

$a^{2}+b^{2}=c\cdot c_{a}+c\cdot c_{b}=c\cdot (c_{a}+c_{b})$

A dosadíme $c_{a}+c_{b}=c$:

$a^{2}+b^{2}=c^{2}$

Pythagorejská čísla

Související informace naleznete také v článku Pythagorejská trojice.

Pythagorejská čísla tvoří trojice přirozených čísel $a,b,c$ takových, že platí $a^{2}+b^{2}=c^{2}$. Jsou to tedy přirozená čísla vyhovující Pythagorově větě. Pythagorejská čísla jsou např. 3, 4 a 5. Pythagorejská čísla lze vytvořit podle následující věty:

Čísla $a,\ b,\ c$, vyjádřená ve tvaru $a=x^{2}-y^{2},\ b=2xy,\ c=x^{2}+y^{2}$ pro nějaká přirozená čísla $x,\ y$ s vlastností $x>y$, jsou pythagorejská.

Pro $x=2,\ y=1$ dostaneme trojici $a=3,\ b=4,\ c=5$.

Pro $x=3,\ y=1$ dostaneme trojici $a=8,\ b=6,\ c=10$.

Jak je zřejmé z výsledků pro první a druhý příklad, jedná se o vícenásobek (v uvedeném případě dvojnásobek) vypočtených hodnot, a tudíž jde o podobné trojúhelníky; proto uvedený způsob generování pythagorejských čísel není dokonalý. Navíc některé existující kombinace nejdou tímto způsobem vůbec vygenerovat.

Odkazy

Literatura

• MAOR, Eli. The Pythagorean Theorem: A 4,000-Year History. Princeton, New Jersey: ‎ Princeton University Press, 2010. ‎ 280 s. ISBN 978-0691148236. (anglicky) 

Externí odkazy

• Obrázky, zvuky či videa k tématu Pythagorova věta na Wikimedia Commons
• Martin Vinkler: Pythagorova věta, Eukleidovy věty, online

Autoritní data	BNE: XX4809534 BNF: cb11946942j (data) GND: 4176546-1 LCCN: sh85109374 NDL: 00934581

Portály: Matematika