Kužel

Tento článek potřebuje úpravy.

Můžete Wikipedii pomoci tím, že ho vylepšíte. Jak by měly články vypadat, popisují stránky Vzhled a styl, Encyklopedický styl a Odkazy.

Obecný kužel.

Rotační kužel (vlevo) a kosý kužel (vpravo).

Kužel je oblé těleso, které získáme jako průnik kuželového prostoru a rovinné vrstvy.

Část kuželové plochy, která tvoří povrch kužele je označována jako plášť kužele. Řez kuželového prostoru hraniční rovinou vrstvy se nazývá podstava. Plášť kužele a podstavu nazýváme společným názvem povrch kužele. Bod, ve kterém se rovinný řez kužele redukuje na bod, se označuje jako vrchol kužele. Kolmou vzdálenost mezi podstavou a vrcholem nazýváme výškou kužele. Vzdálenost mezi vrcholem a podstavou podél pláště nazýváme stranou kužele.

Je-li podstavou kužele kruh, pak jej označíme jako kruhový. Pokud kolmice spuštěná z vrcholu na rovinu podstavy prochází středem podstavy kruhového kužele, pak kužel označujeme jako rotační kužel nebo kolmý kruhový kužel. Pokud kruhový kužel není kolmý, pak jej označujeme jako kosý.

Kuželová plocha a prostor

Kuželový prostor.

Mějme jednoduchou uzavřenou křivku $k$, která leží v rovině. Body, které leží přímkách procházejících libovolným bodem křivky $k$ a bodem $V$ ležícím mimo rovinu křivky $k$ tvoří kuželovou plochu. Část prostoru ohraničená kuželovou plochou se nazývá kuželový prostor.

Kuželová plocha je množina bodů v prostoru, která vznikne z kužele tím, že odstraníme podstavu a každou úsečku pláště (tj. spojnici vrcholu kužele s bodem hranice podstavy) prodloužíme na přímku. Nejlepší představa je taková, že se jedná o dva středově souměrné (podle vrcholu kužele) kornouty jdoucí do nekonečna.

Rovnice

Kuželová plocha (kvadratický kužel) s vrcholem v počátku, která v rovině $z=c$ prochází elipsou $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (tzv. řídící křivka), má rovnici

$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=0$

Přímky, které tvoří povrch kužele se nazývají tvořící přímky.

Tato plocha je asymptotickou plochou (asymptotickým kuželem) hyperboloidů

$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=\pm 1$

Pro $a=b$ jde o rotační kužel s osou rotace $z$.

Kuželovou plochu s vrcholem v bodě $[x_0,y_0,z_0]$ je vždy možné vyjádřit rovnicí

$F\left(\frac{x-x_0}{z-z_0},\frac{y-y_0}{z-z_0}\right)=0$

Vlastnosti

Pro objem kužele platí

$V = \frac{1}{3} \cdot S_p \cdot v$,

kde $S_p$ je obsah podstavy a $v$ je výška kužele.

Rotační kužel

Rotační kužel.

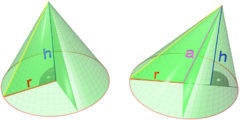
Rotační kužel je rotační těleso vzniklé otáčením pravoúhlého trojúhelníku v prostoru okolo jedné z odvěsen. Otáčením druhé odvěsny vznikne kruhová podstava kužele (někdy také nazývaná jako základna kužele), otáčením přepony pak kuželová plocha nebo jinak plášť kužele. Tento plášť je v podstatě „stočená“ kruhová výseč, jejíž úhel záleží na poměru výšky kužele a poloměru podstavy. Společný vrchol přepony a osy otáčení nazýváme vrchol kužele.

Vlastnosti

Označíme-li $r$ poloměr kruhové podstavy kužele a $h$ výšku kužele (t.j. vzdálenost vrcholu kužele od základny), pak lze vypočítat:

• poloměr pláště (tj. vzdálenost vrcholu kužele od hraniční kružnice podstavy neboli délku strany pláště) pomocí Pythagorovy věty jako

$s = \sqrt{r^2 + h^2} \,\!$

• objem kužele jako

$V = \frac{\pi r^2 h}{3} \,\!$

• povrch kužele jako součet obsahu podstavy $S_p = \pi r^2 \,\!$ a obsahu pláště $S_{pl} = \pi r s \,\!$

$S = S_p + S_{pl} = \pi r (r + s) \,\!$

• Symetrické vlastnosti
  • Kužel není středově souměrný.
  • Kužel je osově souměrný podle spojnice vrcholu kužele se středem podstavy.
  • Kužel je rovinově souměrný podle nekonečně mnoha rovin - rovinou souměrnosti je každá rovina, která v sobě obsahuje jeho osu (tj. vrchol a střed podstavy).

• V jistém smyslu je kužel „limitním případem“ posloupnosti pravidelných n-bokých jehlanů pro n jdoucí do nekonečna. To je ostatně vidět i ze vzorce pro objem, který je hodně podobný vzorci pro objem jehlanu.

Kuželosečky

Související informace naleznete v článku Kuželosečka.

Z geometrického pohledu jsou zajímavé řezy rotační kuželové plochy, tj. průniky této plochy s nějakou rovinou.

Singulární řezy kužele - pokud rovina řezu prochází vrcholem kužele, mohou nastat tři případy:

• průnikem je bod (vrchol kužele), pokud je úhel, který rovina řezu svírá s osou kužele, větší než úhel, který svírají přímky kuželové plochy s její osou
• průnikem je přímka ležící na kuželové ploše, pokud je úhel, který rovina řezu svírá s osou kužele rovný úhlu, který svírají přímky kuželové plochy s její osou
• průnikem jsou dvě přímky, které se protínají ve vrcholu kužele, pokud je úhel, který rovina řezu svírá s osou kužele, menší než úhel, který svírají přímky kuželové plochy s její osou (nebo v případě, kdy je rovina řezu rovnoběžná s osou kužele)

Regulární řezy kužele - pokud rovina řezu neprochází vrcholem kužele, mohou nastat čtyři případy:

• průnikem je kružnice, pokud je rovina řezu kolmá na osu kužele
• průnikem je elipsa, pokud je úhel, který rovina řezu svírá s osou kužele, větší než úhel, který svírají přímky kuželové plochy s její osou, ale rovina řezu není kolmá na osu kužele
• průnikem je parabola, pokud je úhel, který rovina řezu svírá s osou kužele rovný úhlu, který svírají přímky kuželové plochy s její osou
• průnikem je hyperbola, pokud je úhel, který rovina řezu svírá s osou kužele, menší než úhel, který svírají přímky kuželové plochy s její osou (nebo v případě, kdy je rovina řezu rovnoběžná s osou kužele)

To je důvod, proč jsou elipsa, parabola a hyperbola nazývány souhrnně kuželosečkami.

Související články

• Geometrický útvar
• Kvadratická plocha
• Oblá tělesa
• Mnohostěn
• Válec
• Jehlan
• Komolý kužel
• Elipsa
• Parabola
• Hyperbola