Homologická algebra
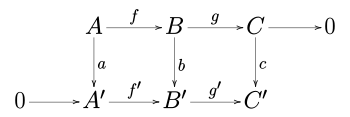
Homologická algebra je obor matematiky, který studuje homologii v obecném algebraickém prostředí. Jedná se o relativně mladou disciplínu, jejíž počátky lze vysledovat k výzkumům v kombinatorické topologii (předchůdci algebraické topologie) a abstraktní algebře (teorii modulů a syzygií) na konci 19. století, především Henriho Poincaré a Davida Hilberta.
Vývoj homologické algebry byl úzce spjat se vznikem teorie kategorií. Z většiny homologická algebra zkoumá homologické funktory a složité algebraické struktury, s nimiž souvisí. Jedním z velmi užitečných a poměrně rozšířených konceptů v matematice jsou řetězcové komplexy, které se dají studovat přes jejich homologii a kohomologii. Homologická algebra poskytuje prostředky k získávání informací obsažených v těchto komplexech a prezentuje je ve formě homologických invariant okruhů, modulů, topologických prostorů a dalších „hmatatelných“ matematických objektů. Mocným nástrojem s tímto účelem jsou spektrální sekvence.
Od samého počátku hrála homologická algebra obrovskou roli v algebraické topologii. Její vliv se postupně rozšířil a v současnosti zahrnuje komutativní algebru, algebraickou geometrii, algebraickou teorii čísel, teorii reprezentace, matematickou fyziku, algebry operátorů, komplexní analýzu a teorii parciálních diferenciálních rovnic. K-teorie je nezávislá disciplína, která čerpá z metod homologické algebry stejně jako nekomutativní geometrie Alaina Connese.
Historie homologické algebry[editovat | editovat zdroj]
Homologická algebra začala být zkoumána ve své nejzákladnější formě v 19. století jako odvětví topologie, ale ve 40. letech se stala nezávislým odvětvím jakožto studium objektů jako například Ext funktor a Tor funktor, mimo ostatní. [1]
Řetězcové komplexy a homologie[editovat | editovat zdroj]
Koncept řetězcových komplexů je v homologické algebře klíčový. Abstraktní řetězcový komplex je posloupnost abelovských grup spojených homomorfismy s tou vlastností, že složení dvou po sobě jdoucích zobrazení je nulové zobrazení:
Prvky z Cn se nazývají n-řetězce a homomorfismy dn se nazývají mezní zobrazení nebo diferenciály. Řetězcové grupy Cn mohou mít další strukturu; mohou to být například vektorové prostory nebo moduly nad daným okruhem R. Diferenciály musí tuto nadrámcovou strukturu zachovávat; musí to pak být například lineární mapy nebo homomorfismy R-modulů. Kvůli pohodlí notace omezme pozornost na abelovské grupy (přesněji na kategorii Ab abelovských grup); slavná věta Barryho Mitchella dokazuje, že všechny výsledky se dají zobecnit na jakoukoli abelovskou kategorii. Každý řetězcový komplex definuje dvě další sekvence abelovských grup: cykly a meze kde a označují jádro a obraz d. Vzhledem k tomu, že složení dvou po sobě jdoucích mezních map je nulové, jsou do sebe tyto množiny vloženy:
Podgrupy abelovských grup jsou automaticky normální, a proto můžeme definovat n-tou homologickou grupu Hn(C) jako podílovou grupu n-cyklů podle n-mezí:
Řetězcový komplex se nazývá acyklický nebo exaktní posloupnost, pokud jsou všechny jeho homologické grupy nulové.
Řetězcové komplexy hojně vznikají v algebře a algebraické topologii. Například jestliže X je topologický prostor, pak jsou singulární řetězce Cn(X) formální lineární kombinace spojitých map ze standardního n-simplexu do X; pokud je K simpliciální komplex, potom jsou simpliciální řetězce Cn(K) formální lineární kombinace n-simplexů z K; pokud je prezentace abelovské grupy A podle generátorů a relací, kde F je volná abelovská grupa překlenutá generátory a R je podgrupa relací, pak lze pomocí C1(A) = R, C0(A) = F, a Cn(A) = 0 pro všechna zbylá n definovat posloupnost abelovských grup. Ve všech těchto případech existují přirozené diferenciály dn, které z Cn dělají řetězcový komplex, jehož homologie odráží strukturu topologického prostoru X, simpliciálního komplexu K nebo abelovské grupy A. V případě topologických prostorů se dostáváme k pojmu singulární homologie, která hraje zásadní roli při zkoumání vlastností těchto prostorů, například variet.
Na filozofické úrovni nás homologická algebra učí, že jisté řetězcové komplexy přidružené k algebraickým nebo geometrickým objektům (topologickým prostorům, simpliciálním komplexům, R-modulům) o nich obsahují množství cenných algebraických informací, přičemž právě homologie je ten nejsnáze dostupný nástroj. Na technické úrovni poskytuje homologická algebra nástroje pro manipulaci s komplexy a získávání těchto informací. Zde jsou dva obecné příklady.
- Dva objekty X a Y jsou propojeny zobrazením f mezi nimi. Homologická algebra studuje vztah, způsobený mapou f, mezi řetězcovými komplexy spojenými s X a Y a jejich homologií. Toto je zobecněno na případ několika objektů a zobrazení, která je spojují. Homologická algebra studuje v jazyce teorie kategorií funktorové vlastnosti různých konstrukcí řetězcových komplexů a homologií těchto komplexů.
- Objekt X připouští více popisů (například jako topologický prostor nebo jako simpliciální komplex) nebo je komplex konstruován s použitím nějaké 'prezentace' X, která vyžaduje nekanonické volby. Je důležité znát vliv změny popisu X na řetězcové komplexy spojené s X. Ten komplex a jeho homologie jsou typicky vzhledem k prezentaci funktoriální, avšak homologie (ačkoli ne komplex sám) je ve skutečnosti nezávislá na zvolené prezentaci, je to invarianta prostoru X.
Standardní nástroje[editovat | editovat zdroj]
Exaktní posloupnosti[editovat | editovat zdroj]
V kontextu teorie grup, posloupnosti
grup a grupových homomorfismů se říká exatní, jestliže obraz (nebo obor hodnot) každého homomorfismu je shodný s jádrem následujícího:
Všimněme si, že taková posloupnost grup a homomorfismů může být konečná i nekonečná.
Podobná definice může být použita i pro některé jiné algebraické struktury. Například lze uvažovat exaktní posloupnost vektorových prostorů a lineárních map nebo modulů a homomorfismů modulů. Obecněji řečeno, koncept exaktní posloupnosti má smysl v každé kategorii s jádry a kojádry.
Krátká exaktní posloupnost[editovat | editovat zdroj]
Nejběžnějším typem exaktní posloupnost je krátká exaktní posloupnost. To je exaktní posloupnost podoby
kde ƒ je monomorfismus a g je epimorfismus. V tomto případě, A je podobjekt B, a odpovídající podíl je izomorfní k C:
(kde ).
Krátkou exaktní posloupnost abelovských grup lze také zapsat jako exaktní sekvenci s pěti členy:
kde 0 představuje nulový objekt, jako je triviální grupa nebo 0rozměrný vektorový prostor. Umístění těchto 0 nutí ƒ být monomorfismem a g epimorfismem (viz níže).
Dlouhá exaktní posloupnost[editovat | editovat zdroj]
Dlouhá exaktní posloupnost je exaktní posloupnost indexovaná přirozenými čísly.
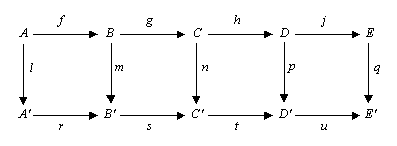
Lemma pěti[editovat | editovat zdroj]
Uvažujme následující komutativní diagram v jakékoliv abelovské kategorii (jako je kategorie abelovských grup nebo kategorie vektorových prostorů nad daným polem) nebo v kategorii grup.
Lemma pěti říká, že pokud jsou řádky exaktní, m a p jsou izomorfismy, l je epimorfismus a q je monomorfismus, pak je n také izomorfismus.
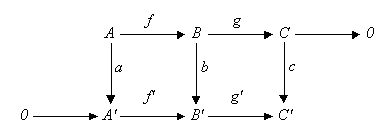
Hadí lemma[editovat | editovat zdroj]
V abelovské kategorii (jako je kategorie abelovských grup nebo kategorie vektorových prostorů nad daným polem) uvažujme komutativní diagram:
kde řádky jsou exaktní posloupnosti a 0 je nulový objekt. Pak existuje exaktní posloupnost vztahující jádra a kojádra z a, b a c:
Pokud je navíc f monomorfismus, pak je i monomorfismus, a pokud je g epimorfismus, pak je taktéž i
Abelovské kategorie[editovat | editovat zdroj]
V matematice je abelova kategorie taková kategorie, v níž se dají sčítat morfismy i objekty a v níž existují jádra a kojádra s žádoucími vlastnostmi. Motivačním příkladem abelovské kategorie je kategorie abelovských grup Ab. Teorie vznikla v předběžném pokusu sjednotit několik kohomologických teorií Alexandera Grothendiecka. Abelovské kategorie jsou velmi stabilní kategorie, například jsou regulární a splňují hadí lemma. Třída abelovských kategorií je uzavřena pod několika kategorickými konstrukcemi, například kategorie řetězcových komplexů z abelovské kategorie nebo kategorie funktorů z malé kategorie do abelovské kategorie je také abelovská. Tyto vlastnosti je v homologické algebře i mimo ni nevyhnutelně podbízejí; tato teorie má hlavní aplikace v algebraické geometrii, kohomologii a čisté teorii kategorií. Abelovské kategorie jsou pojmenovány po Nielsi Henriku Abelovi.
Přesněji, kategorie je abelovská, právě když
- má nulový objekt
- má všechny binární součiny a binární kosoučiny
- má všechna jádra a kojádra
- všechny monomorfismy a epimorfismy jsou normální
Ext funktor[editovat | editovat zdroj]
Nechť R je okruh a nechť ModR je kategorie modulů nad R. Nechť B je v ModR a dejme T(B) = HomR(A, B), pro pevně dané A v ModR. Toto je levý exaktní funktor, a tak má pravé odvozené funktory RnT. Funktor Ext je definován podle
To lze vypočítat tak, že pro jakýkoliv injektivní rozklad:
se spočte:
Poté je (RnT)(B) homologie tohoto komplexu. Všimněme si, že HomR(A, B) není v tom komplexu zahrnut.
Alternativně jej lze definovat pomocí funktoru G(A) = HomR(A, B). Pro pevně daný modul B to je kontravariantní levý exaktní funktor, a tedy dostaneme pravé odvozené funktory RnG a můžeme definovat:
To lze vypočítat výběrem libovolného projektivního rozkladu:
k němuž duálně spočteme:
Poté je (RnG)(A) homologie tohoto komplexu. Znovu si všimněme, že HomR(A, B) je vynechán.
Tyto dvě konstrukce, jak se ukáže, podávají izomorfní výsledky, a proto mohou být obě k výpočtu Ext funktoru použity.
Tor funktor[editovat | editovat zdroj]
Předpokládejme, že R je okruh, a označme R-Mod kategorii levých R-modulů a Mod-R kategorii pravých R-modulů (pokud je R komutativní, obě kategorie splývají). Uvažujme pevně daný modul B v R-Mod. Pro A v Mod-R nastavme T(A) = A ⊗R B. Pak T je pravý exaktní funktor z Mod-R do kategorie abelovských grup Ab (v případě, že je R komutativní, jedná se o pravý exaktní funktor z Mod-R do Mod-R) a jsou pro něj definovány jeho levé odvozené funktory LnT. Stanovujeme:
tj. vezmeme projektivní rozklad:
a odstraníme člen A a roztenzorujeme ten projektivní rozklad spolu s B, abychom získali komplex:
u nějž určíme homologii (všimněme si, že A ⊗R B zde opět nefiguruje; poslední šipka je nulové zobrazení).
Spektrální posloupnost[editovat | editovat zdroj]
Mějme abelovskou kategorii, jako je například kategorie modulů nad okruhem. Spektrální posloupnost je volba nezáporného celého čísla r0 a souboru tří sekvencí:
- pro všechna celá čísla r ≥ r0 máme objekt Er - nazvaný list (jako list papír) nebo někdy také strana nebo člen
- endomorfismy dr : Er → Er splňující dr o dr = 0, nazývané mezní mapy nebo diferenciály
- isomorfismy Er+1 spolu s H(Er), což je homologie Er vzhledem k dr

Tyto dvojsložkové spektrální posloupnosti mají obrovské množství dat na sledování, ale existuje obecná vizualizační technika, která ukazuje strukturu spektrální sekvence jasněji. Máme tři indexy: r, p a q. U každého r si představme, že máme list milimetrového papíru. Na tomto listu budeme brát p jako horizontální směr a q jako vertikální směr. V každém mřížovém bodě máme objekt
Je velmi běžné brát n = p + q jakožto další přirozený index ve spektrální sekvenci. n vede diagonálně, ze severozápadu k jihovýchodu, přes každý list. V homologickém případě mají diferenciály dvojstupeň (−r, r − 1), takže snižují n o jedna. V kohomologickém případě se n o jednu zvyšuje. Když je r nula, diferenciál posouvá objekty o jeden prostor dolů nebo nahoru. Podobně se chovají diferenciály na řetězcovém komplexu. Když je r jedna, diferenciál přesune objekty o jeden prostor doleva nebo doprava. Když je r dva, diferenciál pohybuje objekty stejně jako rytířův pohyb v šachu. Pro vyšší r se diferenciál chová jako zobecněný rytířský pohyb.
Odvozený funktor[editovat | editovat zdroj]
Předpokládejme, že jsme dostali kovariantní levý exaktní funktor F : A → B mezi dvěma abelovskými kategoriemi A a B. Je-li 0 → A → B → C → 0 krátká exaktní posloupnost v A, pak aplikováním F získáme exaktní posloupnost 0 → F(A) → F(B) → F(C) a lze se ptát, jak v této sekvenci pokračovat vpravo, abychom vytvořili dlouhou exaktní posloupnost. Přísně vzato je tato otázka špatně postavená, protože vždy existuje mnoho různých způsobů, jak v dané exaktní sekvenci vpravo pokračovat. Ukazuje se však, že (pokud je A dostatečně „pěkná“) existuje jeden kanonický postup, jak pokračovat - určen pravými funktory odvozenými od F. Pro každé i ≥ 1 existuje funktor RiF : A → B a výše uvedená sekvence pokračuje takto: 0 → F(A) → F(B) → F(C) → R1F(A) → R1F(B) → R1F(C) → R2F(A) → R2F(B) →... . Z toho vidíme, že F je exaktní funktor právě tehdy, když R1F = 0; v jistém smyslu tak odvozené funktory F měří “jak daleko” je F od přesnosti.
Funktorialita[editovat | editovat zdroj]
Spojitá mapa topologických prostorů dává vzniknout homomorfismu mezi jejich n-tými homologickými grupami pro všechna n. Tento základní poznatek z algebraické topologie nachází přirozené vysvětlení prostřednictvím určitých vlastností řetězcových komplexů. Protože je běžné studovat několik topologických prostorů současně, v homologické algebře se často současně zkoumá více řetězcových komplexů.
Morfismus mezi dvěma řetězcovými komplexy, je rodina homomorfismů abelovských grup které komutují s diferenciály v tom smyslu, že pro všechna n. Morfismus řetězcových komplexů dává vzniknout morfismu jejich homologických grup, skládajících se z homomorfismů pro všechna n. Morfismus F se nazývá kvazi-isomorfismus, pokud dává vzniknout isomorfismu na n-té homologii pro všechna n.
Mnoho konstrukcí řetězcových komplexů vznikajících v algebře a geometrii, včetně singulární homologie, má následující vlastnost funktoriality: jestliže dva objekty X a Y jsou spojeny mapou f, pak přidružené řetězcové komplexy jsou spojeny morfismem a navíc složení map f : X → Y a g : Y → Z vyvolává morfismus který se shoduje s kompozicí Z toho vyplývá, že homologické grupy jsou také funktoriální, takže morfismy mezi algebraickými nebo topologickými objekty dávají vzniknout kompatibilním mapám mezi jejich homologií.
Následující definice vychází z typické situace v algebře a topologii. Trojice skládající se ze tří řetězcových komplexů a dvou morfismů mezi nimi se nazývá eexaktní trojice, nebo krátká exaktní posloupnost komplexů a zapisuje se:
pokud pro libovolné n je posloupnost
krátká exaktní posloupnost abelovských grup. Podle definice to znamená, že fn je prosté, gn je surjekce a im fn = ker gn. Jedna z nejzákladnějších vět homologické algebry, někdy známá jako zig-zag lemma, uvádí, že v tomto případě existuje dlouhá exaktní posloupnost v homologii:
kde homologické grupy pro L, M, N a cyklicky následují za sebou, a δn jsou určité homomorfismy určené podle f a g, zvané spojovací homomorfismy. Topologické projevy této věty zahrnují Mayerovu-Vietorisovu sekvenci a dlouhou exaktní posloupnost pro relativní homologii.
Základní aspekty[editovat | editovat zdroj]
Teorie kohomologie byly definovány pro mnoho různých objektů, jako jsou topologické prostory, svazky, grupy, okruhy, Lieovy algebry a C*-algebry. Studium moderní algebraické geometrie by bylo téměř nemyslitelné bez svazkové kohomologie.
V homologické algebře je koncept exaktní posloupnost exaktní; mohou být použity k provádění skutečných výpočtů. Klasickým nástrojem homologické algebry je odvozený funktor; nejzákladnější příklady jsou funktory Ext a Tor.
S ohledem na různorodý soubor aplikací bylo přirozené snažit se obsáhnout všechny tyto případy jednotně. Než se tato oblast ustálila, bylo o sjednocení několik pokusů. Přibližná historie může být uvedena následovně:
- Cartan-Eilenberg: Ve své knize z roku 1956 "Homological algebra" tito autoři použili projektivní a injektivní rozklad modulů.
- Tôhoku: Přístup v oslavovaném dokumentu Alexandera Grothendiecka, který se objevil ve druhé sérii Tohoku Mathematical Journal v roce 1957, používající koncept abelovské kategorie (zahrnutí svazků abelovských grup).
- Odvozená kategorie Grothendiecka a Verdiera. Odvozené kategorie se datují k Verdierově dizertační práci z roku 1967. Jde o příklady triangulovaných kategorií používaných v řadě moderních teorií.
Tyto pak od vypočitatelnosti přešly k obecnosti.
Výpočetní perlík par excellence je spektrální posloupnost; tyto posloupnosti jsou nezbytné v postupech Cartana-Eilenberga a Tohoku, kde jsou potřebné například pro výpočet odvozených funktorů složenin dvou funktorů. Spektrální posloupnosti jsou méně důležité v přístupu pomocí odvozené kategorie, ale stále hrají roli vždy, když jsou nezbytné konkrétní výpočty.
Byly pokusy přijít s "nekomutativní" teorií, která rozšíří první kohomologii jako torzory (důležité v Galoisově kohomologii).
Odkazy[editovat | editovat zdroj]
Reference[editovat | editovat zdroj]
V tomto článku byl použit překlad textu z článku Homological algebra na anglické Wikipedii.
- ↑ History of Homological Algebra, by Chuck Weibel, pp.797-836 in the book The History of Topology, ed. I.M. James, Elsevier, 1999
Literatura[editovat | editovat zdroj]
- Henri Cartan, Samuel Eilenberg, Homological algebra. With an appendix by David A. Buchsbaum. Reprint of the 1956 original. Princeton Landmarks in Mathematics. Princeton University Press, Princeton, NJ, 1999. xvi+390 pp. ISBN 0-691-04991-2
- Alexander Grothendieck, Sur quelques points d'algèbre homologique. Tôhoku Math. J. (2) 9, 1957, 119–221
- Saunders Mac Lane, Homology. Reprint of the 1975 edition. Classics in Mathematics. Springer-Verlag, Berlin, 1995. x+422 pp. ISBN 3-540-58662-8
- Peter Hilton; Stammbach, U. A course in homological algebra. Second edition. Graduate Texts in Mathematics, 4. Springer-Verlag, New York, 1997. xii+364 pp. ISBN 0-387-94823-6
- Gelfand, Sergei I.; Yuri Manin, Methods of homological algebra. Translated from Russian 1988 edition. Second edition. Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2003. xx+372 pp. ISBN 3-540-43583-2
- Gelfand, Sergei I.; Yuri Manin, Homological algebra. Translated from the 1989 Russian original by the authors. Reprint of the original English edition from the series Encyclopaedia of Mathematical Sciences (Algebra, V, Encyclopaedia Math. Sci., 38, Springer, Berlin, 1994). Springer-Verlag, Berlin, 1999. iv+222 pp. ISBN 3-540-65378-3
- WEIBEL, Charles A. An introduction to homological algebra. [s.l.]: Cambridge University Press, 1994. (Cambridge Studies in Advanced Mathematics; sv. 38). ISBN 978-0-521-55987-4. OCLC 36131259
Externí odkazy[editovat | editovat zdroj]
 Obrázky, zvuky či videa k tématu homologická algebra na Wikimedia Commons
Obrázky, zvuky či videa k tématu homologická algebra na Wikimedia Commons