Teserakt

Teserakt (8-nadstěn)
Typ	Pravidelný polychoron
Nadstěn	8 (4.4.4)
Stěn	24 {4}
Hran	32
Vrcholů	16
Uspořádání vrcholů	4 (4.4.4) (tetraedr)
Schläfliho symbol	{4,3,3}
Grupa symetrie	grupa [3,3,4]
Duální těleso	16-nadstěn
Vlastnosti	konvexní

V geometrii je teserakt čtyřrozměrnou analogií krychle, jde tedy o speciální variantu nadkrychle pro d=4. Více odborně by mohl být teserakt definován jako pravidelný konvexní čtyřúhelník s osmi krychlovými nadstěnami. Předpokládá se, že slovo teserakt vymyslel Charles Howard Hinton.

Geometrie

Standardní teserakt je v Euklidovském prostoru dán jako konvexní obal bodů (±1, ±1, ±1, ±1).

Objem a obsah teseraktu

Následující vzorce udávají, jaký je objem teseraktu, a jeho k-rozměrné povrchy (což je vždy obsah k-rozměrné stěny krát počet těchto stěn) v závislosti na hraně a.

$V_{4D}=a^4\,$

$S_{3D}=8\ a^3\,$

$S_{2D}=24\ a^2\,$

$S_{1D}=32\ a\,$

Poloměr vepsané koule je

$\rho=\frac{a}{2}\,$

a poloměr koule opsané je

$r=a\,$

Vícerozměrná geometrická tělesa

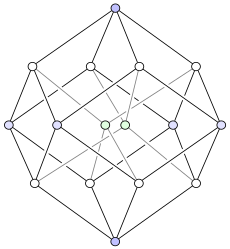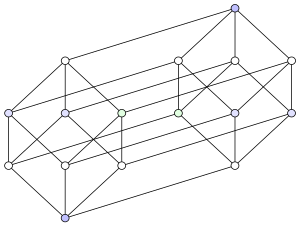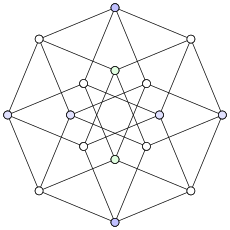
d=2	trojúhelník	čtverec	šestiúhelník	pětiúhelník
d=3	jehlan	krychle, oktaedr	krychloktaedr, kosočtevečný dvanáctistěn	dvanáctistěn, dvacetistěn
d=4	5-nadstěn	teserakt, 16-nadstěn	24-nadstěn	120-nadstěn,600-nadstěn
d=5	5-simplex	penterakt, 5-ortoplex
d=6	6-simplex	hexerakt, 6-ortoplex
d=7	7-simplex	hepterakt, 7-ortoplex
d=8	8-simplex	okterakt, 8-ortoplex
d=9	9-simplex	ennerakt, 9-ortoplex
d=10	10-simplex	dekerakt, 10-ortoplex
d=11	11-simplex	hendekerakt, 11-ortoplex
d=12	12-simplex	dodekerakt, 12-ortoplex
d=13	13-simplex	triskaidekerakt, 13-ortoplex
d=14	14-simplex	tetradekerakt, 14-ortoplex
d=15	15-simplex	pentadekerakt, 15-ortoplex
d=16	16-simplex	hexadekerakt, 16-ortoplex
d=17	17-simplex	heptadekerakt, 17-ortoplex
d=18	18-simplex	oktadekerakt, 18-ortoplex
d=19	19-simplex	ennedekerakt, 19-ortoplex
d=20	20-simplex	ikosarakt, 20-ortoplex

Externí odkazy

• HyperSolids je open source program pro Macintosh (Mac OS X a vyšší).
• Hypercube 98 Program pro Windows zobrazující animovanou 4D hyperkrychli vytvořený Rudy Ruckerem.
• Rozvinutý tvar 4D krychle obsahuje 5× + 17× obrázek