Teorie VSEPR
Teorie VSEPR, plným názvem Valence Shell Electron Pair Repulsion (odpuzování elektronových párů valenční sféry), je model užívaný v chemii k předpovídání geometrie molekul na základě počtu a druhu elektronových párů obklopujících centrální atomy. Je také označován jako Gillespieho-Nyholmova teorie, podle hlavních tvůrců.
Teorie VSEPR je založena na předpokladu, že vazebné i nevazebné elektrony, obklopující atom, se navzájem odpuzují, a proto se snaží zaujmout takové uspořádání, aby byly co nejdále od sebe, čímž určují geometrii molekuly. Gillespie zdůraznil, že odpuzování dané Pauliho vylučovacím principem je pro určování geometrie významnějším faktorem než elektrostatické odpuzování.[1]
Teorie VSEPR je založena spíše na pozorovatelné elektronové hustotě než na vlnové funkci, proto nesouvisí s hybridizací orbitalů, i když obě teorie řeší tvar molekul.[2]
Historie
[editovat | editovat zdroj]Myšlenku, že může existovat vztah mezi geometrií molekuly a počtem valenčních elektronů (jak vazebných, tak i nevazebných), publikoval poprvé v roce 1939 Ryutaro Tsuchida[3] a nezávisle na něm ji v roce 1940 prezentovali Nevil Sidgwick a Herbert Powell z Oxfordské univerzity.[4] V roce 1957 teorii zpřesnili a rozšířili Ronald Gillespie a Ronald Sydney Nyholm z University College London, takže umožňovala výběr mezi různými geometriemi.[5][6]
V posledních letech byla teorie VSEPR kritizována jako zastaralý model, jak z hlediska vědecké přesnosti, tak i z pedagogického úhlu pohledu.[7] Např. u ekvivalentních nevazebných elektronových párů vody a karbonylových sloučenin nejsou uvažovány rozdíly v symetrii (σ vs. π) molekulových orbitalů, a tyto rozdíly jsou někdy v chemii významné. Také neexistují důkazy, ať už výpočetní nebo experimentální, o větší objemnosti nevazebného páru oproti vazebnému. Nicméně, teorie VSEPR věrně popisuje vlastnosti a distribuci elektronů v jednoduchých molekulách, proto je stále vyučována.
Základní přehled
[editovat | editovat zdroj]Teorie VSEPR se využívá pro předpověď uspořádání elektronových párů okolo nevodíkových atomů v molekule, především v jednoduchých a symetrických molekulách, kde jsou tyto centrální atomy vázány ke dvěma a více atomům. Geometrie těchto atomů a uspořádání jejich nevazebných elektronových párů pak určují geometrii zbytku molekuly.
Počet elektronových párů ve valenční slupce centrálního atomu zjistíme nakreslením Lewisova strukturního vzorce molekuly. Teorie VSEPR uvažuje dvojnou a trojnou vazbu jako jednovazebnou skupinu.[8] Součet počtu atomů vázaných k centrálnímu atomu a nevazebných elektronových párů se označuje jako sterické číslo centrálního atomu.
Velikost odpuzování
[editovat | editovat zdroj]Celková geometrie je zpřesňována rozlišením mezi vazebnými a nevazebnými elektronovými páry. Vazebný elektronový pár sdílený v sigma-vazbě s přilehlým atomem leží dále od centrálního atomu než nevazebný pár tohoto atomu, který je blízko kladně nabitého jádra. Teorie VSEPR proto uvažuje odpuzování způsobené nevazebným elektronovým párem za silnější než odpuzování vazebným elektronovým párem. Pokud jsou v molekule dvě interakce s různou velikostí odpuzování, VSEPR předpovídá takovou strukturu, kde bude nevazebný pár umístěn tak, aby odpuzování bylo co nejmenší. Odpuzování dvojice nevazebný pár-nevazebný pár (np-np) je považováno za silnější než nevazebný pár-vazebný pár (np-vp), které je silnější než odpuzování vazebný pár-vazebný pár (vp-vp). Tyto rozdíly pak umožňují určit správnou geometrii, pokud existuje více neekvivalentních pozic.[8] Například, pokud centrální atom obklopuje pět elektronových párů, bude mít molekula tvar trigonální bipyramidy. V tomto uspořádání jsou dva páry v axiální poloze a tři páry v ekvatoriální poloze. Elektronový pár v axiální poloze interaguje s třemi páry, které s ním svírají úhel 90°. Čtvrtý pár pak svírá úhel 180°, jeho interakce s posuzovaným párem je nejslabší. Naproti tomu, elektronový pár v ekvatoriální pozici interaguje s dvěma páry pod úhlem 90° a zbylé dva s ním svírají úhel 120°. Repulze od bližších párů (úhel 90°) je silnější, proto budou nevazebné elektronové páry obsazovat ekvatoriální pozice.[9]
Rozdíl mezi vazebným a nevazebným elektronovým párem lze využít k vysvětlení odchylek od ideální geometrie. Např, v molekule vody jsou čtyři elektronové páry, dva vazebné a dva nevazebné. Výchozím tvarem pro tento počet elektronových párů je tetraedr, v kterém je úhel mezi elektronovými páry 109,5°. Vzhledem k silnější repulzi od nevazebných elektronových párů, dojde k deformaci vazebného úhlu HOH na hodnotu 104,5°.
Toto pravidlo lze ještě rozšířit dvěma dalšími pravidly:
- Bentovo pravidlo: Vazebný elektronový pár s více elektropozitivním ligandem způsobuje větší odpuzování. Tímto lze vysvětlit proč Cl v PClF4 preferuje ekvatoriální pozici a proč je vazebný úhel v OF2 (103,8°) menší než ve vodě (104,5°). Nevazebné páry jsou posuzovány jako speciální případ, kdy má ligand nejvyšší možnou elektropozitivitu.
- Vazba vyššího řádu odpuzuje silněji než vazba nižšího řádu. Tím lze vysvětlit, proč je vazebný úhel O=C-Cl ve fosgenu (124,1°) větší než úhel Cl-C-Cl (111,8°), i když je chlor elektropozitivnější než kyslík.
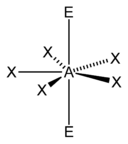
Metoda AXE
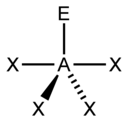
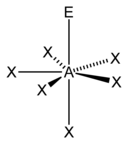
[editovat | editovat zdroj]Metoda AXE se běžně používá pro počítání elektronových párů v teorii VSEPR. Písmeno A představuje centrální atom, X je ligand (atomy vázané k A). Písmeno E reprezentuje počet nevazebných elektronových párů, které náleží centrálnímu atomu molekuly. Součet X a E se označuje jako sterické číslo.
V závislosti na počtu vazebných a nevazebných elektronových párů, dokáže teorie VSEPR předpovědět tvar molekuly, jak je shrnuto v tabulce.
| Sterické číslo |
Geometrie molekuly[10] 0 nevazebných párů |
Geometrie molekuly[10] 1 nevazebný pár |
Geometrie molekuly[10] 2 nevazebné páry |
Geometrie molekuly[10] 3 nevazebné páry |
|---|---|---|---|---|
| 2 | ||||
| 3 |  |
 |
||
| 4 | 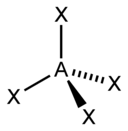 |
 |
 |
|
| 5 |  |
 |
 |
 3 ) |
| 6 | 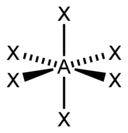 |
 |
 |
|
| 7 |  |
 5 )[11] |
 5 )[12] |
|
| 8 |  8 )[9] |
|||
| 9 | s třemi přidanými vrcholy (ReH 2- 9 )[12] |
| Typ molekuly |
Tvar[10] | Uspořádání elektronových párů[10] včetně nevazebných párů, ty jsou zobrazeny žlutě |
Geometrie[8] bez nevazebných párů |
Příklady |
|---|---|---|---|---|
| AX2E0 | Lineární | BeCl2, HgCl2, CO2 | ||
| AX2E1 | Lomený | 
|

|
NO - 2 , SO2, O3, CCl2 |
| AX2E2 | Lomený | 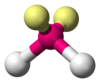
|

|
H2O, OF2 |
| AX2E3 | Lineární | 
|
XeF2, I - 3 , XeCl2 | |
| AX3E0 | Trigonálně planární | 
|

|
BF3, CO 2- 3 , NO - 3 , SO3 |
| AX3E1 | Trigonální pyramida | 
|

|
NH3, PCl3 |
| AX3E2 | Tvar T | 
|

|
ClF3, BrF3 |
| AX4E0 | Tetraedr | 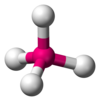
|

|
CH4, PO 3- 4 , SO 2- 4 , ClO - 4 , XeO4 |
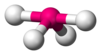
| AX4E1 | Houpačka | 
|
|
SF4 |
| AX4E2 | Čtverec | 
|

|
XeF4 |
| AX5E0 | Trigonální bipyramida | 
|

|
PCl5 |
| AX5E1 | Čtvercová pyramida | 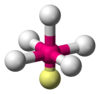
|

|
ClF5, BrF5, XeOF4 |
| AX5E2 | Pětiúhelník | 
|

|
XeF - 5 |
| AX6E0 | Oktaedr | 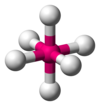
|

|
SF6, WCl6 |
| AX6E1 | Pentagonalní pyramida | 
|

|
XeOF - 5 , IOF 2- 5 |
| AX7E0 | Pentagonalní bipyramida | 
|

|
IF7 |
| AX8E0 | Tetragonální antiprizma | 
|

|
IF - 8 , ZrF 4- 8 , ReF - 8 |
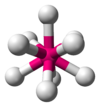
| AX9E0 | Trojboký hranol s třemi přidanými vrcholy |
|

|
ReH 2- 9 [12] |
Reference
[editovat | editovat zdroj]V tomto článku byl použit překlad textu z článku VSEPR theory na anglické Wikipedii.
Literatura
[editovat | editovat zdroj]- KLIKORKA, Jiří; HÁJEK, Bohumil; VOTINSKÝ, Jiří. Obecná a anorganická chemie. 2. vyd. Praha: SNTL 592 s.
Reference
[editovat | editovat zdroj]- ↑ GILLESPIE, Ronald J. Fifty years of the VSEPR model. Coordination Chemistry Reviews. 2008-07-01, roč. 252, čís. 12–14, s. 1315–1327. Dostupné online [cit. 2018-12-29]. ISSN 0010-8545. DOI 10.1016/j.ccr.2007.07.007. (anglicky)
- ↑ GILLESPIE, Ronald J. Teaching Molecular Geometry with the VSEPR Model. Journal of Chemical Education. 2004-03-01, roč. 81, čís. 3, s. 298. Dostupné online [cit. 2018-02-09]. ISSN 0021-9584. DOI 10.1021/ed081p298.
- ↑ TSUCHIDA, Ryutaro. A New Simple Theory of Valency. NIPPON KAGAKU KAISHI. 1939, roč. 60, čís. 3, s. 245–256. Dostupné online [cit. 2018-02-09]. ISSN 0369-4208. DOI 10.1246/nikkashi1921.60.245. (japonsky)
- ↑ SIDGWICK, Nevil V.; POWELL, Herbert M. Bakerian Lecture: Stereochemical types and valency groups. Proc. R. Soc. Lond. A. 1940-10-09, roč. 176, čís. 965, s. 153–180. Dostupné online [cit. 2018-02-09]. ISSN 0080-4630. DOI 10.1098/rspa.1940.0084. (anglicky)
- ↑ GILLESPIE, Ronald J.; NYHOLM, Ronald S. Inorganic stereochemistry. Quarterly Reviews, Chemical Society. 1957-01-01, roč. 11, čís. 4. Dostupné online [cit. 2018-02-09]. ISSN 0009-2681. DOI 10.1039/qr9571100339. (anglicky)
- ↑ GILLESPIE, Ronald J. The electron-pair repulsion model for molecular geometry. Journal of Chemical Education. 1970-01-01, roč. 47, čís. 1, s. 18. Dostupné online [cit. 2018-02-09]. ISSN 0021-9584. DOI 10.1021/ed047p18.
- ↑ CLAUSS, Allen D.; NELSEN, Stephen F.; AYOUB, Mohamed; MOORE, John W.; LANDIS, Clark R.; WEINHOLD, Frank. Rabbit-ears hybrids, VSEPR sterics, and other orbital anachronisms. Chem. Educ. Res. Pract.. 2014-10-08, roč. 15, čís. 4, s. 417–434. Dostupné online [cit. 2018-02-09]. ISSN 1756-1108. DOI 10.1039/c4rp00057a. (anglicky)
- ↑ a b c PETRUCCI, Ralph H.; HARWOOD, William S.; HERRING, Geofrey F. General chemistry : principles and modern applications.. 8. vyd. Upper Saddle River, N.J.: Prentice Hall, 2002. 1 volume (various pagings) s. Dostupné online. ISBN 0130143294. OCLC 46872308
- ↑ a b MIESSLER, Gary L.; TARR, Donald A. Inorganic chemistry. 2. vyd. Upper Saddle River, N.J.: Prentice Hall, 1991. xiii, 642 pages s. Dostupné online. ISBN 0138418918. OCLC 39379369
- ↑ a b c d e f PETRUCCI, Ralph H.; HARWOOD, William S.; HERRING, Geofrey F. General chemistry : principles and modern applications.. 8. vyd. Upper Saddle River, N.J.: Prentice Hall, 2002. 1 volume (various pagings) s. Dostupné online. ISBN 0130143294. OCLC 46872308 S. 413–414.
- ↑ BARAN, Enrique J. Mean amplitudes of vibration of the pentagonal pyramidal XeOF -
5 and IOF 2-
5 anions. Journal of Fluorine Chemistry. Roč. 101, čís. 1, s. 61–63. Dostupné online [cit. 2018-02-16]. DOI 10.1016/s0022-1139(99)00194-3. - ↑ a b c HOUSECROFT, Catherine E.; SHARPE, Alan G. Anorganická chemie. 1. vyd. Praha: Vysoká škola chemicko-technologická v Praze, 2014. 1152 s. ISBN 9788070808726. OCLC 894846634 S. 313–314.
