Optický hranol

Tento článek pojednává o optice. O geometrii pojednává článek hranol.

Rozklad světla hranolem

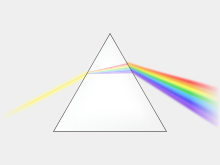
Optický hranol je opticky průhledné těleso s dvěma rovinnými stěnami, které lámou světlo. Světlo při průchodu hranolem mění směr šíření rozkladem (disperzí) a úplným odrazem.

Hranolu využil i Isaac Newton ke zjištění podstaty světla. Při experimentu, kdy umístil za sebe dva trojúhelníkové skleněné hranoly, jež se spojovaly základnami, první hranol rozložil bílé světlo na duhové spektrum, druhý rozložené barvy opětovně sloučil zpět. Díky tomuto pokusu si Newton uvědomil, že bílé světlo není ve své podstatě čisté, jak tvrdil Aristoteles, ale že obsahuje směs všech druhů barev.

Lom světla optickým hranolem

Lom hranolem.

Při průchodu optickým hranolem se světelný paprsek láme dvakrát. Paprsek, který vystupuje z hranolu je od vstupujícího paprsku odchýlen o úhel $\delta$. Tato odchylka je závislá na úhlu dopadu $\alpha_1$, indexu lomu materiálu hranolu a na úhlu $\omega$, který se nazývá lámavý. Tento úhel je sevřen tzv. lámavými stěnami hranolu.

Z obrázku a podle Snellova zákona budou platit vztahy

$\sin\alpha_1 = n\,\sin\beta_1$

$\sin\alpha_2 = n\,\sin\beta_2$

kde $n$ označuje index lomu hranolu. Pro odchylku $\delta$ platí

$\delta = (\alpha_1-\beta_1) - (\alpha_2-\beta_2) = \alpha_1-\alpha_2-\omega$,

neboť platí $\omega=\beta_1-\beta_2$.

Pro malý lámavý úhel $\omega$ jsou malé také úhly $\alpha_1$ a $\alpha_2$. Takový hranol se nazývá optický klín. Pro optický klín mají předchozí rovnice přibližný tvar $\alpha_1=n\beta_1$ a $\alpha_2=n\beta_2$, což umožňuje psát

$\delta = (n-1)\omega$

Pro malý lámavý úhel $\omega$ tedy odchylka $\delta$ nezávisí na úhlu dopadu $\alpha_1$.

Při větších lámavých úhlech však nelze nahradit sinus přímo jeho úhlem. Pokud vyjádříme odchylku $\delta$ jako funkci úhlu lomu $\beta_1$, dostaneme vztah

$\delta = \arcsin(n\,\sin\beta_1) - \arcsin\left[n\,\sin(\beta_1-\omega)\right]-\omega$

Derivací tohoto vztahu podle úhlu lomu $\beta_1$ určíme extrémy, tzn.

$\frac{\mathrm{d}\delta}{\mathrm{d}\beta_1} = \frac{n\,\cos\beta_1}{\sqrt{1-n^2\sin^2\beta_1}} - \frac{n\,\cos(\beta_1-\omega)}{\sqrt{1 - n^2\sin^2(\beta_1-\omega)}} = 0$

Odtud po úpravě získáme podmínku

$(n^2-1)[\sin^2\beta_1-\sin^2(\beta_1-\omega)] = (n^2-1)\sin\omega\,\sin(2\beta_1-\omega) = 0$

Z této podmínky vyplývá, že odchylka $\delta$ má nejmenší hodnotu pro $2\beta_1=\omega$, což podle předchozích vztahů znamená, že nejmenší odchylka se objeví pro

$\beta_1 = \frac{\omega}{2}=-\beta_2\;,\alpha_2=-\alpha_1$

Minimální odchylku tedy získáme tehdy, pokud je paprsek procházející hranolem kolmý k ose souměrnosti lámavého úhlu $\omega$.

Pří minimální odchylce $\delta_m$ bude platit vztah $\alpha_1=\frac{\omega+\delta_m}{2}$. Použitím předchozích vztahů lze pak určit

$\sin\frac{\omega+\delta_m}{2} = n\,\sin\frac{\omega}{2}$

Tento vztah lze využít pro určení indexu lomu materiálu hranolu.

Totální reflexe na hranolu.

U hranolů lze často pozorovat totální reflexi. Tento jev je často využíván např. k převrácení obrazu v dalekohledu apod.

Na hranolu lze také demonstrovat disperzi světla.

Využití

Optické hranoly jsou také používány v optických přístrojích místo klasických zrcadel - využívá se k tomu totálního odrazu a hranoly jsou výhodné pro svou prakticky neomezenou životnost(stříbrná vrstva zaručující funkci zrcadla se sloupe, zmatní, u hranolu není nic, co by mohlo takto přijít k úhoně).

Související články

• Lom světla
• Snellův zákon
• Index lomu
• Hranol