Riemannův součet
Riemannův součet je v matematice určitým druhem aproximace hodnoty určitého integrálu konečným součtem. Je pojmenovaný po německém matematikovi Bernhardu Riemannovi, který žil v devatenáctém století. K jeho nejobvyklejším aplikacím patří aproximace plochy pod grafem funkce, ale umožňuje také další aproximace, např. délky křivek.
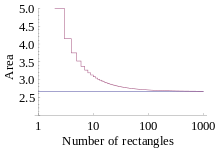
Pro výpočet Riemannova součtu se oblast rozdělí na vhodné tvary (obdélníky, lichoběžníky, plochy omezené obloukem paraboly nebo kubické funkce), jejichž plochu umíme spočítat, a které dohromady ohraničují geometrický útvar, který se blíží útvaru, jehož plocha má být určena. Sečtením plochy všech dílčích útvarů získáme numerickou aproximaci určitého integrálu i když základní věta integrálního počtu neumožňuje nalézt analytické řešení.
Protože oblast vyplněná malými tvary obvykle nemá přesně stejný tvar jako oblast, jejíž plochu máme určit, Riemannův součet nebude přesně rovný velikosti původní plochy. Chybu však lze zmenšovat jemnějším rozdělením oblasti používáním stále menších tvarů. Při tomto zjemňování se součet blíží k Riemannovu integrálu.
Definice[editovat | editovat zdroj]
Nechť je funkce definovaná na uzavřeném intervalu reálných čísel a
- ,
je dělení tohoto intervalu, tj.
- .
Riemannův součet funkce f na intervalu I s dělením P pak definujeme výrazem
kde a [1]. Jaký bod intervalu se použije jako , není důležité, protože hodnoty se blíží k nule, stejně jako rozdíl mezi jakýmikoli dvěma body v intervalu. To je působeno tím, že volba v intervalu je libovolná a tak pro jakoukoli danou funkci f definovanou na intervalu I a pevné dělení P, můžeme vytvářet různé Riemannovy součty v závislosti na tom, jak je zvolen bod , pokud platí .
Některé speciální typy Riemannových součtů[editovat | editovat zdroj]
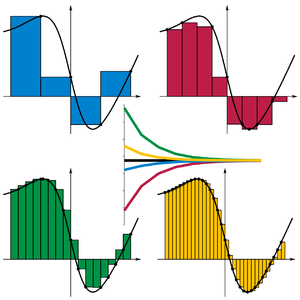
Pro různé volby dostáváme různé typy Riemannových součtů:
- Pokud pro všechna i, pak S se nazývá levý Riemannův součet.[2][3]
- Pokud pro všechna i, pak S se nazývá pravý Riemannův součet.[2][3]
- Pokud pro všechna i, pak S se nazývá nebo středový Riemannův součet (anglicky midpoint rule).[2][3]
- Pokud (tj. supremum funkce f na intervalu ), pak S je horní Riemannův součet nebo horní Darbouxův součet.
- Pokud (tj. infimum funkce f na intervalu ), pak S je dolní Riemannův součet nebo dolní Darbouxův součet.
Všechny tyto volby patří k nejjednodušším metodám numerické integrace. Zhruba řečeno, funkce je Riemannovsky integrovatelná, pokud všechny Riemannovy součty při „zjemňování“ dělení konvergují ke stejné hodnotě.
Průměr levých a pravých Riemannových součtů představuje nejjednodušší z mnoha způsobů aproximace integrálu pomocí vážených průměrů; tento konkrétně se nazývá lichoběžníková metoda. Ke složitějším patří Simpsonova metoda a Newtonovy–Cotesovy vzorce.
Hodnota jakéhokoli Riemannova součtu na daném dělení (tj. pro jakoukoli volbu mezi a ) leží mezi dolním a horním Darbouxovým součtem. Ty jsou základem Darbouxova integrálu, který je ekvivalentní s Riemannovým integrálem.
Metody[editovat | editovat zdroj]
Pro podrobnější rozbor čtyř metod Riemannovy sumace použijeme dělení intervalu na stejné díly. Interval rozdělíme na n podintervalů, každý délky
Body dělení budou
Levý Riemannův součet[editovat | editovat zdroj]
U levého Riemannova součtu aproximujeme hodnotu funkce její hodnotou v levém koncovém bodě. Dostaneme několik obdélníků s základnou velikosti Δx a výškami f(a + iΔx). Celková plocha bude
Levý Riemannův součet přeceňuje skutečnou hodnotu, jestliže f je monotonně klesající na tomto intervalu a podceňuje ji, jestliže funkce je monotonně rostoucí.
Pravý Riemannův součet[editovat | editovat zdroj]

Pokud hodnotu f budeme aproximovat hodnotou v pravém koncovém bodě intervalu, dostáváme obdélníky se základnou Δx a výškami f(a + i Δx). Celková plocha bude
Pokud je f monotonně klesající, pak pravý Riemannův součet skutečnou hodnotu podceňuje; pokud je monotonně rostoucí, pak ji přeceňuje. Chyba součtu bude
- ,
kde je maximální hodnota absolutní hodnoty (derivace f) na daném intervalu.
Středový součet[editovat | editovat zdroj]

Approximace f ve středu intervalů dává pro první interval f(a + Δx/2), pro další f(a + 3Δx/2), atd., až po f(b − Δx/2). Sečtení oblastí dává
- .
Chyba tohoto vzorce bude
- ,
kde je maximální hodnota absolutní hodnoty (druhé derivace f) na daném intervalu.
Lichoběžníková metoda[editovat | editovat zdroj]

V tomto případě jsou hodnoty funkce f na intervalu aproximovány průměrem hodnot v levém a pravém koncovém bodě. Pro výpočet použijeme vzorec pro výpočet plochy lichoběžníka s rovnoběžnými stranami b1, b2 a výškou h:
Celková plocha bude
což je mimochodem průměr levých a pravých součtů této funkce.
Chyba tohoto vzorce je
kde je maximální hodnota absolutní hodnoty .
Riemannův integrál[editovat | editovat zdroj]
Pokud se zabýváme jednorozměrnými Riemannovými součty na intervalu , zjistíme, že pro některé funkce se při zmenšování maximální velikosti dělení k nule (tj. když se limita normy dělení blíží k nule) budou všechny Riemannovy součty konvergovat ke stejné hodnotě. Tuto limitní hodnotu, pokud existuje, nazveme určitým Riemannovým integrálem příslušné funkce na intervalu , tj.
Pokud se maximální velikost dělení zmenšuje k nule, počet podintervalů roste k nekonečnu. Pro každé konečné dělení je Riemannův součet vždy aproximací limitní hodnoty, a tato aproximace se zlepšuje při zjemňování dělení. Následující animace ukazuje, jak zjemňování dělení (při zmenšování velikosti maximálního prvku dělení) lépe aproximuje „plochu“ pod křivkou:
-
Levý součet
-
Pravý součet
-
Středový součet
Protože se předpokládá, že červená funkce je hladká funkce, všechny tři Riemannovy součty budou konvergovat ke stejné hodnotě, když se počet podintervalů blíží k nekonečnu.
Příklad[editovat | editovat zdroj]

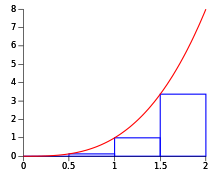
Plochu pod křivkou y = x2 mezi 0 a 2 můžeme v našem příkladě procedurálně vypočítat Riemannovou metodou.
Interval nejprve rozdělíme na n podintervalů, každý o šířce ; což jsou šířky Riemannových obdélníků (zde „boxů“). Protože chceme vypočítat pravý Riemannův součet, posloupnost x-ových souřadnic boxů bude , a tedy posloupnost výšek boxů bude . Při tom platí, že a .
Obsah každého okna bude a proto n-tý pravý Riemannův součet bude
Když uvažujeme limitní případ n → ∞, můžeme dojít k závěru, že se zvětšujícím se počtem boxů se aproximace přibližují skutečné velikosti plochy pod křivkou. Tudíž:
Tato metoda souhlasí s určitým integrálem spočítaným mechaničtějším způsobem:
Protože funkce je na intervalu spojitá a monotonně rostoucí, pravý Riemannův součet přeceňuje integrál o největší hodnotu (zatímco levý Riemannův součet podceňuje integrál o největší hodnotu). Tento fakt, který je intuitivně jasný z diagramů, ukazuje jak povaha funkce určuje, jak přesně integrál je odhadnutý. I když jsou jednoduché, pravý a levý Riemannův součet jsou často méně přesné než pokročilejší techniky odhadu integrálu jako je např. lichoběžníková metoda nebo Simpsonova metoda.
K funkci z tohoto příkladu je snadné nalézt primitivní funkci, takže odhadování integrálu Riemannovými součty je spíše akademické cvičení; ne ke všem funkcím je však možné najít primitivní funkci, takže odhadování jejich integrálů sumací je důležité i prakticky.
Vícerozměrné součty[editovat | editovat zdroj]
Základní myšlenkou za Riemannovým součtem je „rozdělit“ interval na části, znásobit „velikost“ každé části určitou reprezentací hodnoty, kterou funkce nabývá na této části a všechny tyto součiny sečíst. To lze zobecnit tím, že povolíme Riemannovy součty pro funkce na více než jednorozměrném oboru.
Intuitivně je snadné porozumět procesu dělení intervalu, ale technické detaily, jak integrační obor rozdělit, jsou mnohem složitější než v jednorozměrném případě a týkají se aspektů geometrického tvaru integračního oboru[4].
Dvourozměrný případ[editovat | editovat zdroj]
Ve dvourozměrném případě je třeba integrační obor rozdělit na buňky takové, že . Pro každou buňku v dvojrozměrném prostoru pak její „plochu“ označíme [5]. Riemannův součet je
kde .
Trojrozměrný případ[editovat | editovat zdroj]
Ve trojrozměrném prostoru je obvyklé pro integrační obor používat písmeno , takže pro dělení platí , kde je „objem“ buňky indexované . Trojrozměrný Riemannův součet pak lze zapsat jako[6]
kde .
Libovolný počet rozměrů[editovat | editovat zdroj]
K vícerozměrným Riemannovým součtům přejedeme podobně jako od jednorozměrného k dvoj- nebo trojrozměrným součtům. Pro libovolný počet rozměrů n lze Riemannův součet zapsat jako
kde je nějaký bod v n-rozměrné buňce , která má n-rozměrný objem .
Zobecnění[editovat | editovat zdroj]
Velmi obecně lze Riemannovy součty zapsat vztahem
kde je libovolný bod obsažený v prvku dělení a je míra na podkladové množině. Zhruba řečeno, míra je funkce, které udává „velikost“ množiny, v tomto případě velikost množiny ; v jednorozměrném prostoru bývá míra interpretována jako délka intervalu, ve dvourozměrném prostoru jako plocha, v trojrozměrném prostoru jako objem, atd.
Odkazy[editovat | editovat zdroj]
Reference[editovat | editovat zdroj]
V tomto článku byl použit překlad textu z článku Riemann sum na anglické Wikipedii.
- ↑ HUGHES-HALLETT, Deborah; MCCULLUM, William G. Calculus. 4. vyd. [s.l.]: Wiley, 2005. S. 252. (mezi mnoha ekvivalentními variacemi této definice se tento odkaz nejvíce podobá zde uvedené definici.)
- ↑ a b c HUGHES-HALLETT, Deborah; MCCULLUM, William G. Calculus. 4. vyd. [s.l.]: Wiley, 2005. S. 340.
- ↑ a b c OSTEBEE, Arnold; ZORN, Paul. Calculus from Graphical, Numerical, and Symbolic Points of View. 2. vyd. [s.l.]: [s.n.], 2002. Dostupné online. S. M-33.
- ↑ SWOKOWSKI, Earl W. Calculus with Analytic Geometry. 2. vyd. Boston, MA: Prindle, Weber & Schmidt, 1979. Dostupné online. ISBN 0-87150-268-2. S. 821–822.
- ↑ OSTEBEE, Arnold; ZORN, Paul. Calculus from Graphical, Numerical, and Symbolic Points of View. 2. vyd. [s.l.]: [s.n.], 2002. Dostupné online. S. M-34.
- ↑ SWOKOWSKI, Earl W. Calculus s Analytic Geometry. 2. vyd. Boston, MA: Prindle, Weber & Schmidt, 1979. Dostupné online. ISBN 0-87150-268-2. S. 857–858.
Související články[editovat | editovat zdroj]
- Primitivní funkce
- Lebesgueův integrál
- Eulerova metoda a středová metoda, příbuzné metody pro řešení diferenciálních rovnic
- Riemannův integrál, limita Riemannových součtů, pro nekonečně jemné dělení
- Lichoběžníková metoda, numerická metoda založená na použití průměru z levého a pravého Riemannova součtu
- Simpsonova metoda, výkonná numerická metoda účinnější než základní Riemannův součet i lichoběžníková metoda
Externí odkazy[editovat | editovat zdroj]
- Riemannův součet v encyklopedii MathWorld (anglicky)
- Simulace ukazující konvergenci Riemannových součtů
- Vícerozměrný Riemannův integrál a Fubiniova věta materiál k přednášce Martina Klazara, podle 11. kapitoly knihy V. A. Zoricha, Mathematical Analysis II, Springer, 2004

























![{\displaystyle \Delta x\left[f(a)+f(a+\Delta x)+f(a+2\,\Delta x)+\cdots +f(b-\Delta x)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d39698586a053c8cb0750eb693c4f4f824634fc9)
![{\displaystyle \Delta x\left[f(a+\Delta x)+f(a+2\,\Delta x)+\cdots +f(b)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b62a3d74a79890847931dae31aec437b8fe38fbf)



![{\displaystyle \Delta x\left[f(a+{\tfrac {\Delta x}{2}})+f(a+{\tfrac {3\,\Delta x}{2}})+\cdots +f(b-{\tfrac {\Delta x}{2}})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d3f332318381b31a3e68e5e8900e7f4964c0a9e)




![{\displaystyle {\tfrac {1}{2}}\,\Delta x\left[f(a)+2f(a+\Delta x)+2f(a+2\,\Delta x)+2f(a+3\,\Delta x)+\cdots +f(b)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50854a88e6c67f444995d39a8455cefaf2e64dbd)