Lichoběžníková metoda

Lichoběžníková metoda je technika používaná v matematice pro přibližný numerický výpočet určitého integrálu
- .
Jejím principem je aproximace plochy pod grafem funkce lichoběžníkem a použitím jeho plochy jako přibližné hodnoty určitého integrálu funkce na intervalu :
- .
Lichoběžníkovou metodu můžeme považovat za výsledek získaný průměrováním levého a pravého Riemannova součtu a někdy se lichoběžníková metoda takto definuje. Pro získání přesnějšího výsledku se obvykle integrační interval rozděluje na podintervaly, pro každý se spočítá plocha lichoběžníka a výsledky se sečtou. V praxi se „integrováním lichoběžníkovou metodou“ zpravidla myslí tato „zřetězená“ (nebo „kompozitní“) lichoběžníková metoda. Jestliže je dělení intervalu takové, že a je délka -tého podintervalu (tj. ), pak
- .
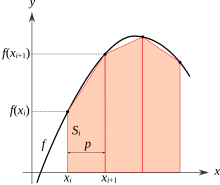
Pro jemnější dělení intervalu bude aproximace přesnější. Často se používá pravidelné dělení, které umožňuje vzorec pro výpočet dále zjednodušit.
Protože se jedná o pouze o aproximaci hodnoty určitého integrálu, je důležité, že na základě vlastností integrované funkce lze určit maximální chybu vypočítané hodnoty.
Historie[editovat | editovat zdroj]
V roce 2016 vyšel článek, který uvádí, že lichoběžníkovou metodu používali již před rokem 50 před naším letopočtem Babyloňané pro výpočet polohy planety Jupiter na ekliptice integrováním její rychlosti.[1]
Numerická implementace[editovat | editovat zdroj]
Nerovnoměrné dělení intervalu[editovat | editovat zdroj]
Je-li dělení intervalu nerovnoměrné, můžeme použít vzorec
Rovnoměrné dělení[editovat | editovat zdroj]
Je-li integrační interval rozdělený na stejně velkých podintervalů, je možné vzorec pro výpočet zjednodušit. Pokud
dostaneme vzorec
Analýza chyb[editovat | editovat zdroj]

Chyba kompozitní lichoběžníkové metody je rozdíl mezi skutečnou hodnotou integrálu a numerickým výsledkem:
Existuje číslo ξ mezi a a b takové, že[2]
To znamená, že pokud je integrand konvexní funkce (a tedy má kladnou druhou derivaci), pak lichoběžníková metoda přeceňuje skutečnou hodnotu (chyba je záporná). To je dobře vidět na kresbě: lichoběžníky pokrývají celou plochu pod křivkou a přesahují ji. Naopak u konkávní funkce dává výpočet menší hodnotu, protože se nepočítá celá plocha pod křivkou. Pokud integrační interval obsahuje inflexní bod, je těžší chybu identifikovat.
Asymptotický odhad chyby pro N → ∞ je
Další členy tohoto odhadu chyby jsou dané Eulerovým–Maclaurinovým sumačním vzorcem.
Pro analýzu chyb lze použít několika technik, mezi něž patří:[3]
- Fourierova řada
- Residuový počet
- Eulerův–Maclaurinův sumační vzorec:[4][5]
- Polynomiální interpolace:[6]
Udává se, že rychlost konvergence lichoběžníkové metody lze používat jako definici třídy hladkosti funkcí.[7]
Důkaz[editovat | editovat zdroj]
Předpokládejme, že a .
Nechť je funkce taková, že je chyba lichoběžníkové metody na jednom z intervalů, . Pak
a
Nyní předpokládejme, že což platí, pokud je dostatečně hladká. Odtud dostáváme
což je ekvivalentní s nebo
Protože a ,
a
Při použití těchto výsledků dostáváme
a
Pokud položíme , dostaneme
Sečtením všech částečných chyb dostáváme
přičemž platí
a
takže
Celková chyba je tedy omezena výrazem
Periodické funkce[editovat | editovat zdroj]
Pro periodické funkce lichoběžníková metoda konverguje velmi rychle. Je to jednoduchý důsledek Eulerova–Maclaurinova sumačního vzorce, který říká, že pokud funkce je -krát spojitě derivovatelná s periodou , pak
kde a je periodické rozšíření -tého Bernoulliho polynomu.[8] U periodických funkcí se derivace v koncových bodech vyruší a jak je patrné ze vzorce, chyba je řádu .
Funkce s jedním vrcholem[editovat | editovat zdroj]
Podobný efekt jako u periodických funkcí se projevuje u funkcí s jedním vrcholem, jako je například Gaussova funkce, exponenciálně modifikovaná Gaussova funkce nebo další funkce, které mají v integračních mezích derivace, které lze zanedbat.[9] Pro výpočet integrálu gaussovské funkce lichoběžníkovou metodou s 1% přesností stačí použít pouze čtyři body.[10] Simpsonovo pravidlo vyžaduje pro dosažení stejné přesnosti 1,8krát více bodů.[10][11]
Přes určité úsilí rozšířit Eulerův–Maclaurinův sumační vzorec na více dimenzí,[12] k přímočařejšímu důkazu velmi rychlé konvergence lichoběžníkové metody v prostorech s mnoha rozměry stačí omezit problém na konvergenci Fourierovy řady. Tímto způsobem lze ukázat, že pokud je periodická na -rozměrném prostoru s spojitými derivacemi, bude rychlost konvergence . Při velmi vysokém počtu dimenzí je integrace Monte-Carlo pravděpodobně lepší volbou, ale pro dvou nebo trojrozměrný případ je efektivní rovnoměrné vzorkování. Toho se využívá při výpočtech ve fyzice pevné fáze, kde rovnoměrné vzorkování přes primitivní buňky v převrácená mřížce je známé jako Monkhorstova-Packova integrace.[13]
„Drsné“ funkce[editovat | editovat zdroj]
U funkcí, které nemají spojitou druhou derivaci, nelze použít výše uvedený odhad chyby. Pro málo hladké funkce je však možné odvodit jiná omezení chyby, která však typicky svědčí, že při zvyšování počtu bodů , v nichž se počítá hodnota integrované funkce je konvergence pomalejší než výše uvedené . Je zajímavé, že v tomto případě má lichoběžníková metoda často ostřejší meze při stejném počtu vyhodnocování funkce než Simpsonovo pravidlo.[14]
Použitelnost a alternativy[editovat | editovat zdroj]
Lichoběžníková metoda patří do skupiny metod pro numerickou integraci nazývaných Newtonovy–Cotesovy vzorce, z nichž Riemannův součet se podobá lichoběžníkovému pravidlu. Jiným členem této skupiny je Simpsonovo pravidlo, které pro funkce mající dvě spojité derivace konverguje obecně rychleji než lichoběžníková metoda, existují však výjimky; u některých tříd méně hladkých funkcí (splňujících slabší podmínky hladkosti) lichoběžníková metoda konverguje obecně rychleji než Simpsonova metoda.[14]
Lichoběžníková metoda je obvykle velmi přesná při integraci periodických funkcí na intervalu shodném s jejich periodou, který lze analyzovat různými způsoby.[7][11] Podobný efekt existuje u funkcí s jedním vrcholem.[10][11]
Metody s nestejně vzdálenými body, jako je Gaussovo kvadraturní pravidlo a Clenshawova–Curtisova kvadratura, jsou však obecně mnohem přesnější pro neperiodické funkce; Clenshawovu–Curtisovu kvadraturu lze považovat za substituci, kterou lze vyjádřit libovolný integrál pomocí periodických integrálů, pro které je lichoběžníková metoda přesnější.
Odkazy[editovat | editovat zdroj]
Poznámky[editovat | editovat zdroj]
- ↑ OSSENDRIJVER, Mathieu. Ancient Babylonian astronomers calculated Jupiter's position from the area under a time-velocity graph. Science. 2016-01-29, roč. 351, čís. 6272, s. 482–484. Dostupné online. DOI 10.1126/science.aad8085. PMID 26823423.
- ↑ Atkinson 1989, equation (5.1.7).
- ↑ Weideman 2002, p. 23, section 2.
- ↑ Atkinson 1989, equation (5.1.9).
- ↑ Atkinson 1989, s. 285.
- ↑ Faires 2011, s. 194.
- ↑ a b Rahman a Schmeisser 1990.
- ↑ KRESS, Rainer, 1998. Numerical Analysis. Svazek 181. [s.l.]: Springer-Verlag. (Graduate Texts in Mathematics).
- ↑ GOODWIN, E. T., 1949. The evaluation of integrals of the form. Mathematical Proceedings of the Cambridge Philosophical Society. Roč. 45, čís. 2, s. 241–245. ISSN 1469-8064. DOI 10.1017/S0305004100024786. (anglicky)
- ↑ a b c KALAMBET, Yuri; KOZMIN, Yuri; SAMOKHIN, Andrey, 2018. Comparison of integration rules in the case of very narrow chromatographic peaks. Chemometrics and Intelligent Laboratory Systems. Roč. 179, s. 22–30. ISSN 0169-7439. DOI 10.1016/j.chemolab.2018.06.001.
- ↑ a b c Weideman 2002.
- ↑ Euler-Maclaurin Summation Formula for Multiple Sums [online]. math.stackexchange.com. Dostupné online.
- ↑ THOMPSON, Nick. Numerical Integration over Brillouin Zones [online]. bandgap.io [cit. 2017-12-19]. Dostupné online.[nedostupný zdroj]
- ↑ a b Cruz-Uribe a Neugebauer 2002.
Reference[editovat | editovat zdroj]
V tomto článku byl použit překlad textu z článku Trapezoidal rule na anglické Wikipedii.
- ATKINSON, Kendall E., 1989. An Introduction to Numerical Analysis. 2. vyd. New York: John Wiley & Sons. ISBN 978-0-471-50023-0.
- RAHMAN, Qazi I.; SCHMEISSER, Gerhard. Characterization of the speed of convergence of the trapezoidal rule. Numerische Mathematik. Prosinec 1990, roč. 57, čís. 1, s. 123–138. ISSN 0945-3245. DOI 10.1007/BF01386402.
- BURDEN, Richard L.; FAIRES, J. Douglas, 2000. Numerical Analysis. 7. vyd. [s.l.]: Brooks/Cole. Dostupné online. ISBN 978-0-534-38216-2.
- WEIDEMAN, J. A. C. Numerical Integration of Periodic Functions: A Few Examples. The American Mathematical Monthly. Leden 2002, roč. 109, čís. 1, s. 21–36. DOI 10.2307/2695765. JSTOR 2695765.
- CRUZ-URIBE, D.; NEUGEBAUER, C. J., 2002. Sharp Error Bounds for the Trapezoidal Rule and Simpson's Rule. Journal of Inequalities in Pure and Applied Mathematics. Roč. 3, čís. 4. Dostupné online.
Související články[editovat | editovat zdroj]
- Gaussovo kvadraturní pravidlo
- Newtonovy–Cotesovy vzorce
- Riemannův součet
- Rombergova metoda
- Simpsonovo pravidlo
- Volterrova integrální rovnice#Numerické řešení pomocí lichoběžníkové metody
Externí odkazy[editovat | editovat zdroj]
 Obrázky, zvuky či videa k tématu lichoběžníková metoda na Wikimedia Commons
Obrázky, zvuky či videa k tématu lichoběžníková metoda na Wikimedia Commons  Kniha en:A-level Mathematics/OCR/C2/Integration#Trapezium_Rule ve Wikiknihách
Kniha en:A-level Mathematics/OCR/C2/Integration#Trapezium_Rule ve Wikiknihách- Trapezium formula. I.P. Mysovskikh – Lichoběžníková metoda v Encyclopedia of Mathematics, ed. M. Hazewinkel
- Notes on the convergence of trapezoidal-rule quadrature Archivováno 9. 2. 2021 na Wayback Machine. – poznámky ke konvergenci výpočtů integrálů lichoběžníkovou metodou
- An implementation of trapezoidal quadrature provided by Boost.Math – implementace kvadratury lichoběžníkovou metod z Boost.Math




















![{\displaystyle {\text{chyba}}=\int _{a}^{b}f(x)\,dx-{\frac {b-a}{N}}\left[{f(a)+f(b) \over 2}+\sum _{k=1}^{N-1}f\left(a+k{\frac {b-a}{N}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd4e23608cad1d376b4719ba0e12070684e6cb6c)

![{\displaystyle {\text{chyba}}=-{\frac {(b-a)^{2}}{12N^{2}}}{\big [}f'(b)-f'(a){\big ]}+O(N^{-3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e857d4aa8d8a4e80d4308b4f364ab5d26d226857)


![{\displaystyle g_{k}(t)={\frac {1}{2}}t[f(a_{k})+f(a_{k}+t)]-\int _{a_{k}}^{a_{k}+t}f(x)dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8ee2c1a6e60c5c3e4f0abcefee8df43cfc4be80)


![{\displaystyle {dg_{k} \over dt}={1 \over 2}[f(a_{k})+f(a_{k}+t)]+{1 \over 2}t\cdot f'(a_{k}+t)-f(a_{k}+t),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0340ea2941deffa7beed8c8595a4aaf897d797bd)














![{\displaystyle \sum _{k=1}^{N}g_{k}(h)={\frac {b-a}{N}}\left[{f(a)+f(b) \over 2}+\sum _{k=1}^{N-1}f\left(a+k{\frac {b-a}{N}}\right)\right]-\int _{a}^{b}f(x)dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99801ff97304978cf8907920a96c7c8e777d9b84)


![{\displaystyle -{\frac {f''(\xi )h^{3}N}{12}}\leq {\frac {b-a}{N}}\left[{f(a)+f(b) \over 2}+\sum _{k=1}^{N-1}f\left(a+k{\frac {b-a}{N}}\right)\right]-\int _{a}^{b}f(x)dx\leq {\frac {f''(\xi )h^{3}N}{12}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2f3d6ee982441634a1ba4a23b22400f4f8f532e)
![{\displaystyle {\text{chyba}}=\int _{a}^{b}f(x)dx-{\frac {b-a}{N}}\left[{f(a)+f(b) \over 2}+\sum _{k=1}^{N-1}f\left(a+k{\frac {b-a}{N}}\right)\right]={\frac {f''(\xi )h^{3}N}{12}}={\frac {f''(\xi )(b-a)^{3}}{12N^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a2576cedaeac41d6b9981e855f6e8d84c461797)








