Umělá neuronová síť

Příklad neuronové sítě: vstup, skrytá vrstva, výstup

Umělá neuronová síť, anglicky Artificial Neural Network či jen Neural Network (ANN, NN), je jeden z výpočetních modelů používaných v oblasti umělé inteligence, podoblasti anglicky tzv. Soft Computing (spolu s evolučními algoritmy a fuzzy logikou). Vzorem je chování neuronů v mozku, od toho je odvozen i název, v současnosti se však princip neuronových sítí od původního zamýšleného napodobení neuronů liší.

Umělá neuronová síť je struktura určená pro distribuované paralelní zpracování dat. Skládá se z umělých (formálních) neuronů, jejichž volným předobrazem je biologický neuron. Neurony jsou vzájemně propojeny synaptickými vazbami a navzájem si předávají signály a transformují je pomocí aktivačních přenosových funkcí. Neuron má libovolný počet vstupů, ale pouze jeden výstup.

Využití

Neuronové sítě se používají mimo jiné pro rozpoznávání obrazů (např. ve formě pixelů) či akustických (např. rozpoznávání řeči) nebo elektrických (např. EKG, EEG) signálů, dále ke klasifikaci, kompresi či segmentaci dat, k predikci vývoje časových řad (např. burzovních indexů), k analýze psaného textu či k filtrování spamu. V lékařství slouží k diagnostice onemocnění či k prohlubování znalostí o fungování informačních systémů (nervových soustav) živých organismů. Například Grossbergova síť vznikla původně jako simulace fyziologického modelu rozpoznávání vzorů na sítnici lidského oka.

Historie

První umělé neurony byly vytvořeny Warrenem McCullochem a Walterem Pittsem v roce 1943. Tyto neurony fungovaly tak, že byl jejich výstup 0 nebo 1 v závislosti na tom, jestli vážená suma vstupních signálů překročila prahovou hranici, nebo ne. Jejich teorie byla, že takový neuron v principu spočte jakoukoli aritmetickou či logickou funkci. Tehdy však nebyla vypracována žádná tréninková metoda.

V padesátých letech přišel Frank Rosenblatt s perceptrony, které doprovázela již i učící pravidla. Perceptrony využíval k rozpoznávání vzorů. Mimo to dokázal, že pokud existují váhy, které zadaný problém řeší, pak k nim učící pravidlo konverguje.

Počáteční nadšení však uvadlo, když se zjištilo, že takovýto perceptron umí řešit pouze lineárně separovatelné úlohy. Frank Rosenblatt se sice snažil model upravit a rozšířit, ale nedařilo se mu to a tak až do osmdesátých let přestal být o perceptrony a neuronové sítě zájem.

V 80. letech došlo k vývoji vícevrstvých perceptronových sítí s asociačními pravidly, schopných aproximovat libovolnou vektorovou funkci, díky čemuž nastala nová vlna zájmu o neuronové sítě, který později částečně upadl kvůli neschopnosti učit sítě o větším počtu vrstev. Až okolo roku 2010 opět došlo k renesanci neuronových síti díky objevu hloubkového učení.

Nejužívanější způsob učení neuronových síti je algoritmus zpětného šíření chyby. Podle různých zdrojů byly základy algoritmu zpětného šíření chyby v kontextu teorie řízení odvozeny z principů dynamického programování; konkrétně se na tom podíleli Henry J. Kelley v roce 1960 a Arthur E. Bryson v roce 1961. Roku 1962 publikoval Stuart Dreyfus jednodušší odvození pomocí řetězového pravidla. Vladimir Vapnik cituje ve své knize o support vector machines článek z roku 1963. V roce 1969 Bryson a Yu-Chi Ho algoritmus popsali jako vícestupňovou optimalizaci dynamických systémů.

V roce 1970 Seppo Linnainmaa publikoval obecnou metodu automatického derivování (AD) diskrétních sítí vnořených diferencovatelných funkcí. Jedná se o moderní variantu metody zpětného šíření chyby, která je efektivní i v řídkých sítích.

V roce 1973 Stuart Dreyfus pomocí zpětného šíření chyby upravoval parametry řídicích systémů úměrně jejich chybovým gradientům. Paul Werbos zmínil možnost uplatnění tohoto principu na umělé neuronové sítě roku 1974 a v roce 1982 tak učinil způsobem, který se používá nyní. O čtyři roky později David E. Rumelhart, Geoffrey E. Hinton a Ronald J. Williams experimentálně prokázali, že tato metoda může vést k užitečným interním reprezentacím vstupních dat v hlubších vrstvách neuronových sítí, což je základem hlubokého učení. V roce 1993 byl Eric A. Wan první, kdo vyhrál pomocí backpropagace mezinárodní soutěž v modelování dat.

V současnosti se neuronové sítě převážně užívají v úlohách zpracování přirozeného jazyka v rámci tzv. jazykových modelů jako např. Word2Vec či Transformer a v úlohách počítačového vidění v rámci tzv. konvolučních neuronových sítí.

Model umělého neuronu

Je popsána celá řada modelů neuronů. Od těch velmi jednoduchých používajících skokové přenosové funkce (perceptron) až po velmi složité popisující každý detail chování neuronu živého organismu, jako např. Hindmarshův–Roseův model neuronu.

Model umělého neuronu s funkcí S

Jedním z nejpoužívanějších je model popsaný McCullochem a Pittsem:

$y=f(\sum _{i=1}^{N}(w_{i}{}x_{i}{})-\vartheta )$

kde:

• $x_{i}{}$ jsou vstupy neuronu
• $w_{i}{}$ jsou synaptické váhy
• $\vartheta$ je práh neuronu
• $f$ je aktivační funkce neuronu
• $y$ je výstup neuronu

Velikost vah $w_{i}{}$ vyjadřuje uložení zkušeností do synapsí neuronu. Čím je vyšší hodnota, tím je daný vstup důležitější. V biologickém neuronu práh $\vartheta$ označuje prahovou hodnotu aktivace neuronu. Tzn. je-li $\sum _{i=1}^{N}(w_{i}{}x_{i}{})$ menší než práh, je neuron pasivní (inhibovaný) a je-li $\sum _{i=1}^{N}(w_{i}{}x_{i}{})$ větší než práh, je neuron aktivní (excitovaný).

Aktivační funkce neuronu

Aktivační (přenosová) funkce neuronu v umělých neuronových sítích definuje výstup neuronu při zadání sady vstupů neuronu. Nelineární aktivační funkce umožňují neuronovým sítím řešit nelineární problémy. Klasická nelineární aktivační funkce je sigmoida (logistická funkce) o parametrech strmosti (určující šířku pásma citlivosti neuronu na svůj aktivační potenciál) a prahové hodnoty (určující posunutí počátku funkce) spolu s jejími limitními tvary jako je linearita pro strmost blížící se nule resp. ostrá nelinearita (skoková funkce) pro strmost blížící se nekonečnu:

$f(x)={1 \over (1+e^{-p(x-\vartheta )})}$, tj. $\lim _{p\rightarrow 0}f(x)={1 \over 2}$ resp. $\lim _{p\rightarrow \infty }f(x)=0$ pro $x<0$ a $\lim _{p\rightarrow \infty }f(x)=1$ pro $x>0$

Aktivační funkce. V levém sloupci sigmoida spolu se svými limitními případy, v pravém sloupci možné transformace dat přiváděných na vstupní resp. výstupní neurony.

Volbou aktivační funkce neuronů vstupní resp. výstupní vrstvy neuronové sítě můžeme určit způsob transformace dat na síť přiváděných:

• Sigmoida: $f(x)=(1+e^{-p(x-\vartheta )})^{-1}$ - z ad 1) a ad 2) (viz níže) plyne $p={\ln 0,95-\ln 0,05 \over 3\sigma }\cong {1 \over \sigma }$

ad 1) z $0,95=(1+e^{-3p\sigma })^{-1}$ plyne $e^{-3p\sigma }={0,05 \over 0,95}$

ad 2) z $0,05=(1+e^{3p\sigma })^{-1}$ plyne $e^{3p\sigma }={0,95 \over 0,05}$

• Gaussova křivka: $g(x)=e^{-p(x-\vartheta )^{2}}$ - z $0,05=e^{-p6\sigma ^{2}}$ plyne $p=-{\ln 0,05 \over 6\sigma ^{2}}\cong {1 \over 2\sigma ^{2}}$

• Mexický klobouk: $h(x)=-\sigma ^{2}g''(x)$ - uvedené transformaci resp. její nezáporné části odpovídají různá pásma citlivosti.

Parametry uvedených transformací mají následující význam:

ϑ – střední hodnota dat přiváděných na daný neuron z trénovací množiny

σ – směrodatná odchylka dat přiváděných na daný neuron z trénovací množiny

Kromě uvedených aktivačních funkcí se užívají ještě jejich různé modifikace:

• Identita – linearita modifikovaná posunutím středu symetrie do počátku
• Hyperbolická tangenta – rozšíření oboru hodnot sigmoidy na interval od -1 do +1
• ReLU – složení ostré linearity (vlevo od počátku) s identitou (vpravo od počátku)
• Radiální báze – Gaussova křivka resp. Mexický klobouk

Architektury sítě

Příklady architektury neuronových sítí: rekurentní autoasociativní paměť RAM, samorganizující síť SOM, vícevrstvý perceptron MLP.

Podle způsobů propojení neuronů existuje více různých architektur neuronových sítí, neurony se řadí do jednotlivých vrstev umístěných nad sebou:

Dopředná neuronová síť:

• Lineární heteroasociativní paměť – dvouvrstvá síť
• Perceptron – pouze jeden neuron
• Vícevrstvý perceptron – libovolný počet skrytých vrstev (minimálně třívrstvá síť)
• Samoorganizující síť – dvouvrstvá síť

Rekurentní neuronová síť:

• Lineární autoasociativní paměť – jednovrstvá síť
• Nelineární autoasociativní paměť (Hopfieldova) – jednovrstvá síť
• Nelineární heteroasociativní paměť (Bidirektní) – dvouvrstvá síť
• Grossbergova či ART dvouvrstvá síť spojitého času

Učení sítě

Cílem učení neuronové sítě je nastavit síť tak, aby dávala co nejpřesnější výsledky. V biologických sítích jsou zkušenosti uloženy v synapsích. V umělých neuronových sítích jsou zkušenosti uloženy v jejich matematickém ekvivalentu – váhách vazeb neuronů. Učení neuronové sítě rozlišujeme na učení s učitelem (supervised learning) a učení bez učitele (unsupervised learning). Fáze učení neuronové sítě bývá nazývána adaptivní, fáze vybavování po naučení neuronové sítě bývá nazývána aktivní. Adaptace vah vázajících neurony závisí na jejich stavech aktivace. V případě učení s učitelem jsou stavy výstupních neuronů sítě aktivovány na ně přiloženým vnějším stimulem (výrokem učitele), v případě učení bez učitele si stavy výstupních neuronů síť nastaví v závislosti na stavech vstupních neuronů sama, a to pomocí aktivní dynamiky sítě, tj. každý krok adaptivní dynamiky je proložen průběhem dynamiky aktivní.

Učení s učitelem

Při učení s učitelem trénovací data sestávají ze vstupních objektů (vektorů jejich parametrů, tj. nezávisle proměnných) a jejich požadovaných výstupních ohodnocení, tj. závisle proměnných (obecně také ve tvaru vektorů), tj. výroků učitele o objektu. Podobně jako v biologických sítích je zde využita zpětná vazba. Neuronové síti je předložen vzor. Na základě aktuálního nastavení sítě je zjištěn aktuální výsledek. Ten porovnáme s vyžadovaným výsledkem a určíme chybu. Poté spočítáme nutnou korekci (dle typu neuronové sítě) a upravíme hodnoty vah tak, abychom snížili hodnotu chyby. Toto opakujeme až do dosažení námi stanovené povolené chyby. Poté je síť adaptována. Naučená funkce sítě pak dokáže odhadovat výstupní ohodnocení každého vstupního objektu, i neobsaženého v trénovacích datech, tj. musí umět zobecnit (generalizovat) souvislost mezi vstupy a výstupy danou příklady obsaženými v trénovacích datech. U neuronových sítí se učení s učitelem užívá vícevrstvého perceptronu.

Pozn.: Pokud se vstupní objekty shodují s požadovanými výstupními ohodnoceními, mluvíme o tzv. samoučení (self-supervised learning), tj. síť (např. autoenkodér) se pak učí tzv. autoasociativní fuknkci.

Rozdíl mezi učením s učitelem (učitel označí, zda je objekt čtverec či trojúhelník) a bez učitele (síť podobné objekty nashlukuje, aniž by věděla jak se značí)

Učení bez učitele

Na rozdíl od učení s učitelem při učení bez učitele nejsou v trénovacích datech vstupní objekty provázané s jejich ohodnocením, tj. schází výrok učitele a učení bez učitele tedy vykazuje samoorganizaci sítě, která zachycuje vstupní vzory jako hustotu pravděpodobnosti. Během učení bez učitele si stavy výstupních neuronů síť nastaví sama v závislosti na stavech vstupních neuronů, nevyhodnocujeme tedy správnost výsledku, síť si vstupní vzory sama třídí přizpůsobením své konfigurace. Vzory třídí do skupin a reaguje dle jejich typického zástupce. U neuronových sítí se učení bez učitele užívá u kompetičních sítí, které si výrok učitele nahrazují tzv. laterální inhibicí.

Pozn.: Kombinaci učení s učitelem a učení bez učitele označujeme jako semi-supervised learning.

Míra změn vah po jednotlivých vrstvách, daná tlumením zpětného šíření chyby, tj. první tři vrstvy se neučí prakticky vůbec, smysluplně se učí pouze poslední tři.

Hluboké učení

Hluboké učení je učení neuronových sítí s velkou hloubkou. Hloubkou sítě se myslí počet vrstev neuronů, které jsou propojeny tak, že výstup jedné vrstvy je vstupem vrstvy následující. U hlubokého učení se hloubka sítě nachází často v řádech desítek a více vrstev. Pro odhad parametrů sítě (trénování) se obvykle používá algoritmus zpětného šíření chyby. Trénování probíhá ve dvou fázích, tj. nejprve předučení sítě dopředným směrem např. pomocí autoenkodérů (samoučení) a poté doučení sítě zpětným směrem (učení s učitelem), eliminuje se tak tlumení zpětného šíření chyby. Metodologie hlubokého učení se prosadila kolem roku 2010 jako základní možnost pro řešení složitých problémů strojového učení jako je klasifikace obrazů, mluvené či psané řeči nebo překlady z jednoho přirozeného jazyka do jiného.

Model synaptické vazby ohodnocené vahou w mezi vstupním a výstupním neuronem s úrovní aktivace x a y.

Hebbovské učení

Hebbův princip učení je způsob určování vah vzájemných orientovaných vazeb mezi umělými neurony jako ukládání úrovně aktivace vstupního neuronu vážené úrovní aktivace výstupního neuronu do váhy vazby mezi vstupním a výstupním neuronem. Váha vazby mezi oběma neurony se pak zvyšuje, pokud se oba neurony aktivují synchronně, a snižuje, pokud se aktivují asynchronně. Neurony, které jsou buď oba pozitivně aktivní současně nebo oba negativně aktivní současně, mají silné pozitivní váhy vzájemné vazby, zatímco ty, které jsou současně opačně aktivní, mají silné negativní váhy vzájemné vazby. Hebbovské učení se užívá u asociativních pamětí, jako je např. Hopfieldova či bidirektní síť.

Přeučení

Přeučení je stav, kdy je systém příliš přizpůsoben množině trénovacích dat, ale nemá schopnost generalizace a selhává na validační množině dat, tj. vykazuje sice minimální chybu na tréninkové množině, ale na validační množině vykazuje zcela chybné výsledky. To se může stát např. při malém rozsahu trénovací množiny nebo pokud je síť příliš mohutná (např. příliš mnoho neuronů skrytých vrstev resp. počet skrytých vrstev v síti). Řešením je zvětšení počtu prvků trénovací množiny, snížení mohutnosti sítě nebo snížení počtu parametrů hodnoceného objektu, které v důsledku snižuje složitost učené funkce sítě. Krajním řešením je předčasné ukončení učení (průběžné sledování chyby na validační množině a konec učení ve chvíli, kdy se chyba na této množině dostane do svého minima).

Trénovací data

Data určená pro učení neuronové sítě se skládají ze vstupních vektorů dat a v případě učení s učitelem z odpovídajících vstupních vektorů dat. Pro správné naučení neuronové sítě je obvykle potřeba dostatečně reprezentativní množství trénovacích dat. Neuronová síť aproximuje funkci, která ze vstupního vektoru vypočítá výstupní vektor a podle rozdílu od správného výstupního vektoru upraví své vnitřní parametry. Tento proces se opakuje, dokud není systém dostatečně naučen. Při učení se používají trénovací data, validační data či testovací data. Tato data mají být disjunktní. Pomocí trénovacích dat probíhá vlastní učení, podle chování na validačních datech se kontroluje přeučování a na testovacích datech se určuje úspěšnost chování naučené sítě na nových, neznámých datech. Trénovací data se tedy dle způsobu užití dělí do tří skupin:

• Trénovací množina je sada dat, ve které učící algoritmus nachází určitý vztah mezi vstupy a výstupy, tj. provádí jejich regresní analýzu.

• Validační množina je sada dat, která se používají pro případnou úpravu parametrů učení ve snaze vyhnout se jeho přeučení. Systém je správně naučený tehdy, jestliže se shodnou úspěšností vyhodnocuje trénovací množinu i validační množinu. Pokud má vyhodnocení trénovací množiny výrazně vyšší úspěšnost, je systém přeučený.

• Testovací množina je sada dat, která se používají pro ověření kvality naučeného systému.

V případě učení bez učitele se trénovací data skládají pouze ze vstupních vektorů dat obsažených v trénovací množině.

Algoritmus zpětného šíření chyby

Gradientní sestup - vpravo nahoře naznačeno uváznutí v lokálním minimu

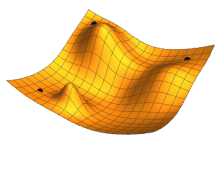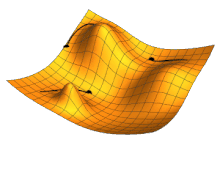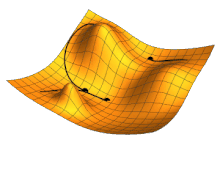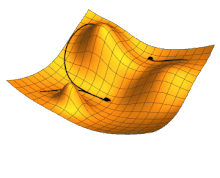
Algoritmus zpětného šíření chyby (Error backpropagation algorithm) je typická metoda učení umělých neuronových sítí. Používá se u vícevrstvých sítí při učení s učitelem, tedy pokud je na množině příkladů použitých k učení vždy znám požadovaný výsledek. Zpětné šíření chyby je založeno na metodě gradientního sestupu.

Kvalita naučení umělé neuronové sítě je popsána chybovou funkcí, nejčastěji kvadratickou chybou:

$E\;=\;{\frac {1}{2}}\sum \limits _{j=1}^{N}\sum \limits _{i=1}^{n}(z_{ij}-y_{ij})^{2}\;=\;\sum \limits _{j=1}^{N}E_{j}$, pak $\Delta w\;=\;-\alpha {\partial E_{j} \over \partial w}$

$E$ – chyba

$N$ – počet vzorů předložených síti

$n$ – počet neuronů výstupní vrstvy

$z_{ij}$ – požadovaný výstup daného neuronu a daného vzorku

$y_{ij}$ – vypočítaný výstup daného neuronu a daného vzorku

$\Delta w$ – vektor přírůstků vah gradientního kroku

$\alpha$ – velikost gradientního kroku

Zpětné šíření chyby

Jeden sestupný gradientní krok pak může vypadat následovně:

$w_{ij}\left(T\right)=w_{ij}\left(T-1\right)+\alpha \ y_{i}\left(T\right)\ g_{j}(x_{j}(T))+\mu \ \Delta w_{ij}\left(T-1\right)$

${\vartheta }_{i}\left(T\right)={\vartheta }_{i}\left(T-1\right)+\alpha \ g_{i}(x_{i}(T))+\mu \ \Delta {\vartheta }_{i}\left(T-1\right)$

$p_{i}\left(T\right)=p_{i}\left(T-1\right)+\alpha \ x_{i}\left(T\right)\ g_{i}(x_{i}(T))+\mu \ \Delta p_{i}\left(T-1\right)$

$g_{k}(x_{k})=p_{k}y_{k}(1-y_{k})(z_{k}-y_{k})\ \ \ \ \ g_{i}(x_{i})=p_{i}y_{i}\left(1-y_{i}\right)\sum _{j}{g_{j}(x_{j})\ w_{ij}}$

$k\in V_{M},j\in V_{L},i\in V_{L-1},L\in \left\{2,\dots ,M\right\},T\in \left\{1,\dots ,N\right\}$

$x_{i}$ – potenciál i-tého neuronu

$y_{i}$ – skutečný stav i-tého neuronu

$z_{i}$ – požadovaný stav i-tého neuronu

$g_{i}$ – adaptační funkce i-tého neuronu

$p_{i}$ – strmost aktivační funkce i-tého neuronu

$\vartheta _{i}$ – práh i-tého neuronu

$w_{ij}$ – váha vazby i-tého neuronu s j-tým neuronem

$\alpha$ – velikost gradientního sestupného kroku

$\mu$ – míra setrvačnosti gradientního sestupu

$V_{L}$ – populace neuronů L-té vrstvy

$M$ – počet vrstev sítě

$\Delta$ – předcházející přírůstek příslušné proměnné

Cílem učení je minimalizovat chybovou funkci závislou na vstupních vahách neuronů, přičemž gradientní sestup obecně najde pouze lokální minimum, proto se do gradientního sestupu zavádí jistá jeho setrvačnost, spočívající v míře respektování směru jeho minulého sestupného kroku, tj. k aktuálnímu gradientu se připočte minulý gradient a aktuální sestupný krok se provede ve směru jejich součtu. Tato deformace gradientního sestupu pak umožní vyklouznutí z mělkého lokálního minima. Učení neuronové sítě spočívá ve změně vah vstupů neuronů. Algoritmus zpětného šíření chyby v každém kroku postupuje v následujících třech fázích:

• Aplikují se učící vzory a pro každý vzor se postupně směrem vpřed napočítají výstupy (vstupní signál se sítí šíří směrem dopředu).
• Napočítané výstupy se porovnají s požadovanými výstupy, tj. spočte se chyba, jak byla popsána výše.
• Na základě spočtené chyby se počítají hodnoty adaptačních funkcí ve směru od poslední vrstvy k první vrstvě (pro výpočet hodnoty adaptačních funkcí podřazené vrstvy již musí být vypočteny hodnoty adaptačních funkcí nadřazené vrstvy), tj. spočítá se gradient chybové funkce, na základě kterého se provede sestupný gradientní krok, tj. upraví se vstupní váhy neuronů tak, že klesne hodnota chyby. Výpočet tedy postupuje zpětně od výstupní vrstvy až po vstupní vrstvu (odtud zpětné šíření chyby), váhy se mění podle jejich vlivu na chybu.

Odkazy

Související články

• Modulární neuronová síť
• Elmanova Jordanova neuronová síť
• Polynomiální neuronová síť

Externí odkazy

• Obrázky, zvuky či videa k tématu umělá neuronová síť na Wikimedia Commons
• Umělá neuronová síť v České terminologické databázi knihovnictví a informační vědy (TDKIV)
• Předpovídání pomocí neuronové sítě – včetně Java appletu pro experimenty s předpovídáním funkce

Autoritní data	NKC: ph115443 TDKIV: 000000120 GND: 4226127-2 LCCN: sh90001937 LNB: 000053170 NDL: 01165604 NLI: 987007551192405171

Portály: Informační věda a knihovnictví