Coriolisova síla


Coriolisova síla je setrvačná síla působící na tělesa, která se pohybují v rotující neinerciální vztažné soustavě tak, že se mění jejich vzdálenost od osy otáčení. Coriolisova síla má směr kolmý ke spojnici těleso – osa otáčení a způsobuje stáčení trajektorie tělesa proti směru otáčení soustavy (v případě pohybu tělesa od středu otáčení. Pokud se těleso pohybuje směrem ke středu otáčení, působí síla ve směru otáčení. Například na těleso padající volným pádem nad rovníkem působí Coriolisova síla směrem k východu, tedy po směru otáčení). Patří mezi zdánlivé síly (nekoná práci). Je pojmenována po Gaspardu Gustavu de Coriolisovi, který se silami v rotujících soustavách zabýval v 19. století. Ovšem tento koncept již roku 1651 popsal i Giovanni Battista Riccioli.[1]
Působení Coriolisovy síly se označuje jako Coriolisův efekt. Jedná se o viditelné odchylování přímočaře se pohybujících objektů od přímého směru, pokud je pozorujeme z neinerciální vztažné soustavy. Na Zeměkouli se jakákoliv hmota díky rotaci Země, pohybující se ve směru poledníků, odklání na severní polokouli doprava, na jižní polokouli pak doleva. Významné a jasně viditelné jsou projevy Coriolisovy síly v meteorologii. Na severní polokouli se otáčejí tlakové níže vždy doleva a tlakové výše doprava, na jižní přesně opačně. Coriolisova síla má vliv i na mořské proudy.
Výpočet[editovat | editovat zdroj]
Vektorový vztah pro Coriolisovo zrychlení (zrychlení částice v rotujícím systému) je
neboli (po vynásobení hmotností) vztah pro Coriolisovu sílu
kde Fc je Coriolisova síla, m je hmotnost tělesa, v je vektor rychlosti tělesa v neinerciální vztažné soustavě, ω je vektor úhlové rychlosti otáčení soustavy a označuje vektorový součin. Velikost Coriolisovy síly spočteme jako
kde je úhel sevřený mezi vektorem úhlové rychlosti a vektorem rychlosti.
Ze vzorce vyplývá, že Coriolisova síla je kolmá na směr pohybu tělesa a na osu otáčení. Pro její směr platí:
- pokud je vektor rychlosti rovnoběžný s osou otáčení, Coriolisova síla je nulová
- pokud vektor rychlosti směřuje kolmo k ose otáčení, Coriolisova síla působí ve směru rotace
- pokud vektor rychlosti směřuje kolmo od osy otáčení, Coriolisova síla působí proti směru rotace
- pokud vektor rychlosti směřuje po směru otáčení, Coriolisova síla působí směrem od osy
- pokud vektor rychlosti směřuje proti směru otáčení, Coriolisova síla působí směrem k ose
Pokud bychom uvažovali určité místo na Zemi o zeměpisné šířce a soustavu souřadnic, jejíž osa x směřuje na východ, osa y na sever a osa z směrem vzhůru, potom úhlovou rychlost, rychlost tělesa a Coriolisovu sílu vypočítáme jako:
Díky vertikální složce Coriolisovy síly jsou tělesa v pohybu na východ odchylovány nahoru (nadlehčovány), v pohybu na západ jsou odchylovány dolů. Tento jev je známý jako Eötvösův efekt. V praxi není jev příliš pozorovatelný, protože je zanedbatelný v porovnání s působením gravitace a tlaku. Zjednodušením předchozích vztahů na horizontální rovinu je (uvažujeme vz = 0):
- kde se nazývá Coriolisův parametr.
Příčiny[editovat | editovat zdroj]
Coriolisův efekt existuje jen v rotující vztažné soustavě. Neodpovídá žádnému skutečnému zrychlení nebo síle, ale pouze jeho zdání z pohledu rotujícího vztažného systému.
Projev Coriolisovy síly na objektu v pohybu může být interpretován jako součet dvou stejně velkých efektů s různými příčinami:
- První příčina je změna rychlosti tělesa v čase. Neměnná rychlost (v inerciální vztažné soustavě, kde platí běžné fyzikální zákony) představuje dvě různé rychlosti ve dvou různých okamžicích z pohledu rotující soustavy. Zrychlení, které se projevuje, je úměrné úhlové rychlosti vztažné soustavy (rychlost, s jakou mění osy souřadnic svou polohu) a rychlosti tělesa. Odtud vztah . Znaménko minus je dáno definicí vektorového součinu (pravidlo pravé ruky) a znaménkovou konvencí vektoru úhlové rychlosti.
- Druhá příčina je změna rychlosti v prostoru. Různé body rotující soustavy mají různé rychlosti (z pohledu inerciální vztažné soustavy). Aby se objekt pohyboval po přímé dráze, musí mít určité zrychlení, které způsobuje od jednoho bodu k druhému změnu rychlosti stejnou, jaká je změna rychlosti ve vztažné soustavě. Tento efekt je úměrný úhlové rychlosti (která určuje relativní rychlost dvou různých bodů rotující vztažné soustavy) a rychlosti tělesa kolmo na osu rotace (která určuje, jak rychle se těleso pohybuje mezi těmito body). Odtud opět vztah .
Co Coriolisův efekt není[editovat | editovat zdroj]
- Coriolisova síla není důsledek zakřivení Země, pouze její rotace. Nicméně velikost Coriolisovy síly je závislá na zeměpisné šířce a tato závislost je způsobená tvarem Země.
- To, že pohyb balistických střel a družic zakreslený na běžných mapách světa zdánlivě opisuje zakřivenou trajektorii, je zapříčiněno především sférickým tvarem Země. Nejkratší vzdálenost mezi dvěma body na zemském povrchu obvykle není na takových mapách rovná úsečka. Každá dvourozměrná mapa nevyhnutelně zkresluje zakřivený (trojrozměrný) zemský povrch. Typicky (například v běžně používaném Mercatorovu zobrazení) se zkreslení zvyšuje v blízkosti pólů. Zakřivení trajektorie by se na mapách objevilo i kdyby se Země neotáčela. Coriolisův efekt se na balistických raketách pochopitelně projevuje, ale na mapách je mnohem méně zřetelný než zkreslení použitého zobrazení.
- Coriolisova síla by neměla být zaměňována s odstředivou silou. V rotující soustavě vždy působí na těleso (pokud jej nemůžeme považovat za hmotný bod ležící na ose otáčení) odstředivá síla, ať už je v pohybu nebo ne. Vznik Coriolisova efektu vyžaduje, aby se těleso pohybovalo relativně k rotující soustavě rychlostí, jejíž vektor v není rovnoběžný s osou otáčení. Zvláště pokud v leží na tečně ke kružnici se středem na ose otáčení, která je na ní kolmá, vektor Coriolisovy síly je rovnoběžný s vektorem odstředivé síly. V takovém případě lze uvažovat rotující vztažnou soustavu s jinou úhlovou rychlostí, kde rychlost v je nulová a Coriolisova síla taktéž.
- Není pravda, že se v důsledku Coriolisova efektu voda vypouštěná z vany nebo umyvadla stáčí vždy v jednom směru na severní polokouli a v opačném směru na jižní polokouli.[2][3] Ve skutečnosti je působení Coriolisovy síly o několik řádů menší než různé náhodné vlivy (například tvar nádoby, počáteční proudění vody) a jev je měřitelný pouze v laboratorních podmínkách. Prvně tento jev publikoval Ottokar Tumlirz roku 1908. Pověru rozšířily i některé televizní seriály (například Akta X[4], Simpsonovi). Navíc se toto nesprávné tvrzení objevilo v několika vědeckých programech a publikacích.[5] Jedná se tak o vědecký mýtus.
Demonstrace Coriolisova efektu[editovat | editovat zdroj]

K demonstraci působení Coriolisovy síly lze použít mělkou otočnou plochu s parabolickým dnem. V nádobě s rovným dnem by setrvačnost vytlačila tělesa na okraj rotující nádoby, avšak pokud má nádoba správný parabolický tvar a otáčí se správnou rychlostí, potom složka gravitační síly ve směru tečny k parabole je v rovnováze s dostředivou silou nutnou k zachování rychlosti a poloměru zakřivení plochy. To umožňuje pozorovat působení Coriolisovy síly izolovaně.

Kotouče odřízlé z válce suchého ledu se pohybují po povrchu nádoby téměř bez tření, takže jejich pohyb ovlivňuje pouze Coriolisova síla. Kamera připevněná k otočné nádobě rotuje společně s ní a zachycuje pohyb z pohledu rotující soustavy. Protože se soustava otočí několikrát za minutu (na rozdíl od Země, která se otočí jednou za den), Coriolisova síla je mnohem větší a lépe se pozoruje v krátkém čase a na malém prostoru.
Působení Coriolisovy síly lze též názorně a snadno doložit pomocí Foucaultova kyvadla, které bylo prvním jasně viditelným důkazem rotace Země.
Coriolisova síla v meteorologii[editovat | editovat zdroj]

Mezi nejdůležitějších projevy Coriolisovy síly patří dynamika oceánu a atmosféry. V meteorologii je vhodné používat rotující vztažnou soustavu, kde Země zůstává nehybná. Proto se zavádí zdánlivá odstředivá a Coriolisova síla. Nicméně odstředivá síla je vyrušená díky tvaru Země – ustálil se jako rotační elipsoid tak, aby gravitační a odstředivá síla byly v rovnováze. Proto pouze Coriolisova síla má zřetelný dopad na výpočty.
Proudění v okolí tlakové níže[editovat | editovat zdroj]
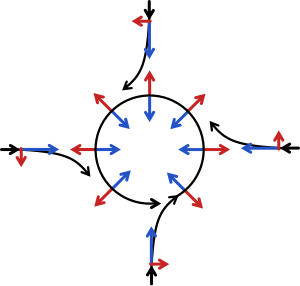
Pokud v atmosféře vznikne tlaková níže, vzduch proudí směrem k ní, ale Coriolisova síla jej odchyluje ve směru kolmém na rychlost. Systém se dostane do rovnováhy ve vířivém pohybu. Protiváhu ke Coriolisově síle, jež působí směrem od tlakové níže, tvoří síla způsobená rozdílem tlaku.
Místo aby vzduch proudil přímo do tlakové níže, ve velkém měřítku má atmosféra a oceán sklon pohybovat se kolmo ke směru poklesu tlaku. Jev je známý jako geostrofický vítr. Na planetě, která se neotáčí, by tekutiny proudily po nejkratší možné dráze tak, aby vyrovnaly rozdíly v tlaku. Za povšimnutí stojí, že geostrofická rovnováha se velmi liší od „setrvačných pohybů“, což vysvětluje proč jsou cyklóny ve středních zeměpisných šířkách o řád větší, než by způsobilo samotné setrvačné proudění.
Způsob, jakým se proudění odklání, a směr pohybu se nazývá Buys-Ballotovo pravidlo. Na severní polokouli směřuje pohyb okolo tlakové níže proti směru hodinových ručiček. Na jižní polokouli směřuje po směru ručiček; dynamika otáčení je zde zrcadlový odraz severu. Cyklóny se nevytváří na rovníku, protože v tamějších oblastech je Coriolisův parametr příliš malý.
Další vlivy na Zemi[editovat | editovat zdroj]
Coriolisův efekt ve velkém měřítku velmi ovlivňuje oceánské a atmosférické proudy, což vede ke vzniku jevů, jako je například tryskové proudění (jet stream). Takové jevy jsou v geostrofické rovnováze, což znamená, že Coriolisova síla a síla působící díky gradientu tlaku jsou v rovnováze. Coriolisův efekt také zodpovídá za šíření mnoha druhů vln v oceánu i atmosféře včetně Rossbyho vln a Kelvinovy vlny.[zdroj?]
Další projevy Coriolisovy síly[editovat | editovat zdroj]
Coriolisův průtokoměr[editovat | editovat zdroj]
Coriolisův průtokoměr je přístroj na měření hmotnostního průtoku kapaliny trubicí a její hustoty. Princip přístroje, který představila v roce 1977 společnost Micro Motion, je založený na rezonančním kmitání trubice, kterou kapalina protéká. Vibrace poskytují rotující soustavu, ve které se projevuje Coriolisův efekt. Coriolisovy průtokoměry jsou velmi přesné a jejich měření nezávisí na dalších vlastnostech kapaliny.[6] Tyto průtokoměry se používají k měření průtoku odebraných pohonných hmot na čerpacích stanicích.
Molekulová fyzika[editovat | editovat zdroj]
Ve víceatomových molekulách se pohyb popisuje pomocí rotace molekuly a kmitů atomů okolo jejich rovnovážných poloh. Výsledkem kmitů je pohyb atomů relativní k rotující vztažné soustavě molekuly. Proto zde vystupuje Coriolisova síla a odchyluje pohyb atomů ve směru kolmém k původním kmitům.
Balistika[editovat | editovat zdroj]
Coriolisův efekt má význam ve vnější balistice při výpočtu trajektorie střel dlouhého doletu. Nejznámější příklad z historie je Pařížské dělo, jež používali Němci za první světové války k ostřelování Paříže ze vzdálenosti 120 km. Coriolisova síla hraje roli téměř ve všech dnešních výpočtech trajektorie střely. Efekt je třeba brát v úvahu i při střelbě z odstřelovací pušky dlouhého dosahu.
Zvířata[editovat | editovat zdroj]

Dvoukřídlí (diptera) a motýli (Lepidoptera) využívají Coriolisovu sílu při letu: kyvadélka u dvoukřídlých, respektive tykadla u motýlů rychle kmitají a hmyz je využívá jako vibrační gyroskopy. V tomto případě Coriolisův efekt nesouvisí s rotací Země.
Existuje též teorie, která zdůvodňuje sklon delfínů ke kroužení na levou, respektive pravou stranu, když spí. Proti této teorii je též řada námitek.[7] Přesto může jít o pohyb po tzv. inerciálních kružnicích.
Lidé[editovat | editovat zdroj]
Vliv Coriolisovy síly lze pozorovat i na tvaru oděvu u tance dervišů.[8]
Vodní toky[editovat | editovat zdroj]
Řeky tekoucí na severní polokouli vymílají více pravý břeh, řeky tekoucí na jižní polokouli pak břeh levý.[9] V důsledku toho řeky v měkkém podloží vytvářejí meandry.[zdroj?] Zjevné je to při pohledu na tvar sibiřských řek.[zdroj?]
Odkazy[editovat | editovat zdroj]
Reference[editovat | editovat zdroj]
V tomto článku byl použit překlad textu z článku Coriolis effect na anglické Wikipedii.
- ↑ CAMPBELL, Macgregor. Coriolis-like effect found 184 years before Coriolis. newscientist.com [online]. 2011-01-14 [cit. 2021-10-16]. Dostupné online. (anglicky)
- ↑ SHAPIRO, Ascher. Film Notes for Vorticity [online]. [cit. 2010-02-04]. S. 5, 6. Dostupné online. (anglicky)
- ↑ SHAPIRO, Ascher H. Bath-Tub Vortex. S. 1080–1081. Nature [online]. 1962-12-15. Roč. 196, čís. 4859, s. 1080–1081. Dostupné online. DOI 10.1038/1961080b0. (anglicky)
- ↑ Emery, C. Eugene, Jr. 'X-Files' coriolis error leaves viewers wondering. Encyclopedia.com [online]. 1995-01-05 [cit. 2007-09-16]. Dostupné online. (anglicky)
- ↑ Bad Coriolis [online]. [cit. 2007-12-22]. Dostupné online. (anglicky)
- ↑ ORLÍKOVÁ, Soňa. Měření průtoku tekutin - principy průtokoměrů [online]. [cit. 2007-12-22]. Dostupné v archivu pořízeném dne 2008-11-03.
- ↑ PETR, Jaroslav. Delfíni – pravotočiví a levotočiví. OSEL. 2004-09-24. Dostupné online [cit. 2007-12-22].
- ↑ A Whirling Dervish puts physicists in a spin. phys.org [online]. 2013-11-26. Dostupné online. (anglicky)
- ↑ HOUSER, Pavel. Jak se točí víry a jaký břeh podemílají řeky?. scienceworld.cz [online]. 2001-07-30. Dostupné online.
Související články[editovat | editovat zdroj]
- Buys-Ballotovo pravidlo
- Dynamika
- Eötvösův efekt
- Foucaultovo kyvadlo
- Gustave Gaspard de Coriolis
- Mechanika
- Rossbyho číslo
Externí odkazy[editovat | editovat zdroj]
 Obrázky, zvuky či videa k tématu Coriolisova síla na Wikimedia Commons
Obrázky, zvuky či videa k tématu Coriolisova síla na Wikimedia Commons  Galerie Coriolisova síla na Wikimedia Commons
Galerie Coriolisova síla na Wikimedia Commons- REICHL, Jaroslav; VŠETIČKA, Martin. Coriolisova síla. Encyklopedie fyziky [online]. 1995-01-05 [cit. 2007-09-16]. Dostupné online.
- ev. Coriolisovy průtokoměry Micro Motion společnosti Emerson. Automatizace. 2004-09-24, roč. 49, čís. 9. Dostupné online [cit. 2007-12-22].
- BEZDĚK, Alexej; KOVAŘÍK, Fanda. Coriolisova síla. Torricelliho pokus. Brnkačka [online]. [cit. 2007-12-22]. Dostupné online.














