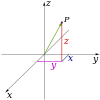Sférická soustava souřadnic

Sférická soustava souřadnic (kulová soustava souřadnic) je soustava souřadnic v prostoru, u které jedna souřadnice (označovaná $r$) udává vzdálenost bodu od počátku souřadnic, druhá souřadnice (označovaná $\varphi$) udává úhel odklonu průvodiče bodu od osy $x$ a třetí souřadnice (označovaná $\theta$) úhel mezi průvodičem a osou $z$.

Sférická soustava souřadnic je vhodná v případech takových problémů, které mají sférickou symetrii. Tyto mají zpravidla ve sférických souřadnicích podstatně jednodušší tvar.

Bod ve sférické soustavě souřadnic.

Transformace sférických souřadnic na kartézské:

$x = r \sin{\theta} \cos{\varphi}$

$y = r \sin{\theta} \sin{\varphi}$

$z = r \cos{\theta}\,$

Převod kartézských souřadnic na sférické:

$r = \sqrt{x^2 + y^2 + z^2},$

$\varphi = \operatorname{arctg2}(y,x),$

$\theta = \arccos\left(\frac{z}{r}\right),$

kde arctg2(x,y) je zobecnění funkce arkus tangens. Úhly volíme v rozsahu $0\leq\theta\leq\pi$ a $0\leq\varphi<2\pi$.

Délka infinitesimální úsečky se spočte jako

$\mathrm{d}s^2=\mathrm{d}r^2+r^2\mathrm{d}\theta^2 + r^2 \sin^2 \theta\ \mathrm{d}\varphi^2.$

Objem infinitesimálního elementu prostoru spočteme jako

$\mathrm{d}V=r^2 \left|\sin\theta\right|\mathrm{d}r\,\mathrm{d}\varphi\,\mathrm{d}\theta,$

takže celkový objem spočteme integrací tohoto výrazu přes danou oblast vyjádřenou ve sférických souřadnicích.