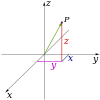Kartézská soustava souřadnic

Body v rovinné kartézské soustavě souřadnic

Kartézská soustava souřadnic je taková soustava souřadnic, u které jsou souřadnicové osy vzájemně kolmé přímky, které se protínají v jednom bodě – počátku soustavy souřadnic. Jednotka se obvykle volí na všech osách stejně velká. Jednotlivé souřadnice polohy tělesa je možno dostat jako kolmé průměty polohy k jednotlivým osám.

V prostoru má kartézská soustava souřadnic 3 vzájemně kolmé osy (běžně označované x, y, z), v rovině 2 kolmé osy (x, y).

Historie

Soustava je pojmenována podle francouzského matematika a filozofa Reného Descarta (1596–1650), latinsky Cartesius (proto „kartézská“), který se zasloužil (kromě jiného) o propojení algebry a eukleidovské geometrie. Nezávisle na něm byly souřadnice objeveny i matematikem Pierrem de Fermatem, který také uvažoval ve třech dimenzích, svůj objev ale nepublikoval. Ještě před Descartem a Fermatem používal konstrukce podobné kartézským souřadnicím filozof a teolog Mikuláš Oresme († 1382), profesor pařížské univerzity.

Pravotočivá a levotočivá soustava prostorových kartézských souřadnic

Pravidlo pravé ruky

Porovnání pravidel pravé a levé ruky

Představte si, že v místě, kde stojíte, je počátek prostorové kartézské soustavy. Osa x nechť směřuje vpravo, osa y nechť směřuje vpřed (směrem, kterým se díváte) a osa z nechť směřuje vzhůru. Taková soustava se nazývá pravotočivá souřadná soustava (v angličtině right handed).

Určení, zda je soustava pravotočivá či levotočivá, usnadňuje pravidlo pravé ruky.

Zaměníme-li osy x a y, získáme souřadnicovou soustavu levotočivou (v angličtině left handed). Příklad pravotočivé soustavy je na obrázku.

Obvykle se pracuje s pravotočivou souřadnicovou soustavou.

Definice

Číselná osa

Nejjednodušší kartézskou soustavou je číselná osa. Jedinou souřadnicí každého bodu je jeho vzdálenost od počátku. Zápis je jednoduchý – například A=[0] nebo L=[−5]. Je potřeba brát ohled na znaménko.

Dvě dimenze – rovina

V rovině tvoří kartézskou soustavu dvě vzájemně kolmé osy, které se protínají v počátku. Souřadnicemi bodu jsou jeho vzdálenosti od osy y (souřadnice x, vodorovná, abscisa) a od osy x (souřadnice y, svislá, ordináta). V obrázku jsou zakresleny čtyři body se svými souřadnicemi, které se obvykle zapisují ve tvaru (x, y), dají se tedy chápat také jako vektory, orientované úsečky spojující počátek s body. Délka vektoru čili vzdálenost bodu od počátku se vypočte pomocí Pythagorovy věty.

V matematice, fyzice a strojírenství je první osa obvykle definována nebo znázorněna jako vodorovná a orientovaná doprava a druhá osa je svislá, orientovaná směrem vzhůru. Počátek je často označen jako 0 a dvě souřadnice jsou často označeny písmeny X a Y nebo x a y. Osy pak mohou být označovány jako osa X a osa Y. Výběr písmen pochází z původní konvence, kdy se má použít druhá část abecedy pro značení neznámých hodnot, zatímco první část abecedy k značení hodnot známých. Ve vztahu k osám x,y je poloha libovolného bodu v dvourozměrném prostoru dána uspořádanou dvojicí reálných čísel, přičemž každé číslo udává vzdálenost tohoto bodu od počtu jednotek měřených podél dané osy. Souřadnice jsou obvykle psány jako dvě čísla v závorkách A=[a₁;a₂] – bod A [souřadnice na ose x, souřadnice na ose y].

Obě osy rozdělí rovinu na čtyři pravé úhly, oblasti nazvané kvadranty. Kvadrant může být pojmenován nebo číslován různými způsoby, ale kvadrant, kde jsou všechny souřadnice kladné, se obvykle nazývá první kvadrant.

Bod v prostorové pravotočivé kartézské soustavě souřadnic

Dalším široce používaným souřadnicovým systémem je polární souřadnicový systém, kde hraje roli vzdálenost od počátku a úhel.

Tři dimenze

V (třírozměrném) eukleidovském prostoru tvoří kartézskou soustavu souřadnic tří navzájem kolmé osy, protínající se v počátku [0,0,0]. Stejně jako v dvojrozměrném případě se každá osa stává číselnou čárou. Pro libovolný bod prostoru se jedná o rovinu, která je kolmá ke každé ose souřadnic v konkrétním místě. Kartézskými souřadnicemi jsou tři čísla ve zvoleném pořadí.

Neexistují standardní názvy souřadnic ve třech osách (někdy se však používají výrazy abscisa, ordináta a aplikáta). Souřadnice jsou často označeny písmeny X, Y, Z (nebo x, y, z). Pak se podle toho mohou označovat roviny XY, YZ a XZ.

V matematice a fyzice jsou první dvě osy často definovány nebo zobrazovány jako horizontální, přičemž třetí osa směřuje nahoru. V takovém případě může být třetí souřadnice označována jako výška/nadmořská výška.

Bod v třírozměrném prostoru značíme A=[a₁;a₂;a₃]. Místo písmene A můžeme vybrat jakékoli písmeno. Například bod K ležící na souřadnicích [1;2;3]. Souřadnice bodu jsou jeho vzdálenosti od tří rovin, které se protínají v osách x, y, z.

Kvadranty a oktanty

Čtyři kvadranty v kartézské soustavě souřadnic

Osy dvojrozměrného kartezského systému rozdělují rovinu na čtyři nekonečné oblasti tzv. kvadranty, které jsou ohraničeny ze stran poloosami. Kvadranty se značí římskými číslicemi a proti směru hodinových ručiček, začíná se od pravého horního ("severovýchodního") kvadrantu, viz obrázek napravo.

V každém z kvadrantů je x,y kladné nebo záporné: I (+, +), II (−, +), III (−, −) a IV (+, −).

Podobné rozdělení je i u trojrozměrného systému, prostor se ovšem dělí do osmi částí – oktantů. Označení určitého oktantu tvoří znaménka tří souřadnic, např. (+ + +) nebo (− + −). Zobecnění kvadrantu a oktantu na libovolný počet rozměrů je anglicky orthant a platí pro něj obdobný systém označení.

Externí odkazy

• Obrázky, zvuky či videa k tématu kartézská soustava souřadnic na Wikimedia Commons
• Kartézská soustava souřadnic na Mathworld
• Nástroj k výkladu souřadnic
• Interaktivní transformátor souřadnic

Autoritní data	PSH: 2932 GND: 4370913-8

Portály: Matematika