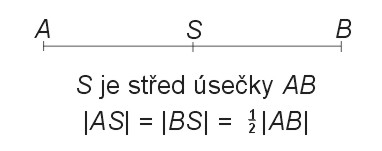Úsečka

Úsečka je část přímky mezi dvěma body.

Určující body úsečky se nazývají krajní body úsečky.

Značení

Úsečka se znázorňuje rovnou čarou mezi jejími krajními body, zapisuje se pomocí svých krajních bodů, případně malým písmenem.

Vlastnosti

Velikost úsečky neboli délka úsečky se většinou zapisuje pomocí dvou svislých čar (rovné závorky), např. $|AB|$.

Střed úsečky je bod, který leží na úsečce a jehož vzdálenost od obou krajních bodů je stejná.

Osa úsečky je přímka kolmá k úsečce procházející jejím středem. Všechny body na ose úsečky mají od obou krajních bodů stejnou vzdálenost.

Úsečka je středově souměrná podle svého středu. Úsečka je osově souměrná, má dvě osy souměrnosti: jedna osa souměrnosti je osa úsečky, druhou osou souměrnosti je přímka, na níž úsečka leží.

V některých případech bývá bod považován za úsečku s nulovou délkou.

Úsečka jako průnik dvou polopřímek.

Úsečku lze také považovat za průnik dvou opačných polopřímek.

Související články

• Matematika
• Geometrie
• Lineární geometrické útvary
• Přímka
• Interval
• Hypocykloida

Externí odkazy

• Obrázky, zvuky či videa k tématu úsečka ve Wikimedia Commons
• Slovníkové heslo úsečka ve Wikislovníku