Rovnoběžník Rovnoběžník (latinsky parallelogrammum , někdy též r(h)omboid ; ve starší české literatuře kosodélník ) je čtyřúhelník , jehož protilehlé strany jsou rovnoběžné .
Protější strany rovnoběžníku jsou shodné (mají stejnou délku) :
a
=
|
A
B
|
=
|
C
D
|
=
c
,
d
=
|
A
D
|
=
|
B
C
|
=
b
.
{\displaystyle a=|AB|=|CD|=c,\qquad d=|AD|=|BC|=b.}
Protější úhly rovnoběžníku jsou shodné. Součet velikostí vnitřních úhlů čtyřúhelníku je 360°, součet dvou sousedních úhlů je 180°.
Velikost protilehlých úhlů má stejnou velikost, platí
α
=
∠
D
A
B
=
∠
B
C
D
=
γ
,
β
=
∠
A
B
C
=
∠
C
D
A
=
δ
.
{\displaystyle \alpha =\angle DAB=\angle BCD=\gamma ,\qquad \beta =\angle ABC=\angle CDA=\delta .}
středem souměrnosti . Úhlopříčka rozděluje rovnoběžník na dva shodné trojúhelníky.
Úhlopříčky rovnoběžníku se vzájemně půlí. Délky úhlopříček se počítají podle vzorce:
e
=
|
A
C
|
=
a
2
+
d
2
+
2
a
d
cos
α
=
(
a
+
h
a
cotg
α
)
2
+
h
a
2
,
{\displaystyle e=|AC|={\sqrt {a^{2}+d^{2}+2ad\cos \alpha }}={\sqrt {(a+h_{a}{\mbox{cotg}}\,\alpha )^{2}+h_{a}^{2}}}\,,}
f
=
|
B
D
|
=
a
2
+
d
2
−
2
a
d
cos
α
=
(
a
−
h
a
cotg
α
)
2
+
h
a
2
.
{\displaystyle f=|BD|={\sqrt {a^{2}+d^{2}-2ad\cos \alpha }}={\sqrt {(a-h_{a}{\mbox{cotg}}\,\alpha )^{2}+h_{a}^{2}}}\,.}
Rovnoběžník je středově souměrný , středem souměrnosti je průsečík jeho úhlopříček.
Shrnutí vlastností čtyřúhelníků. [1]
ROVNOBĚŽNÍKY
čtverec obdélník kosočtverec kosodélník
všechny strany jsou stejně dlouhé
sousední strany mají různé délky
všechny strany jsou stejně dlouhé
sousední strany mají různé délky
všechny vnitřní úhly jsou pravé
žádný vnitřní úhel není pravý
úhlopříčky se navzájem půlí
úhlopříčky mají stejnou délku
úhlopříčky mají různé délky
úhlopříčky jsou k sobě kolmé
úhlopříčky nejsou k sobě kolmé
úhlopříčky jsou k sobě kolmé
úhlopříčky nejsou k sobě kolmé
úhlopříčky půlí vnitřní úhly
úhlopříčky nepůlí vnitřní úhly
úhlopříčky půlí vnitřní úhly
úhlopříčky nepůlí vnitřní úhly
Obsah rovnoběžníku je roven:
S
=
a
h
a
=
b
h
b
=
a
b
sin
α
{\displaystyle S=ah_{a}=bh_{b}=ab\sin \alpha }
kde
a
=
|
A
B
|
{\displaystyle a=|AB|}
b
=
|
A
D
|
{\displaystyle b=|AD|}
h
a
{\displaystyle h_{a}}
A
B
{\displaystyle AB}
h
b
{\displaystyle h_{b}}
A
D
{\displaystyle AD}
α
{\displaystyle \alpha }
Pokud jsou vrcholy
A
,
B
,
C
,
D
{\displaystyle A,B,C,D}
A
=
(
x
A
,
y
A
)
{\displaystyle A=(x_{A},y_{A})}
B
=
(
x
B
,
y
B
)
{\displaystyle B=(x_{B},y_{B})}
absolutní hodnotě determinantu sestaveného ze souřadnic libovolných tří vrcholů takto
S
=
|
det
(
x
B
−
x
A
x
D
−
x
A
y
B
−
y
A
y
D
−
y
A
)
|
=
|
(
x
B
y
D
−
x
D
y
B
)
−
(
x
A
y
D
−
x
D
y
A
)
+
(
x
A
y
B
−
x
B
y
A
)
|
.
{\displaystyle S=\left|\det \left({\begin{array}{cc}x_{B}-x_{A}&x_{D}-x_{A}\\y_{B}-y_{A}&y_{D}-y_{A}\end{array}}\right)\right|=|(x_{B}y_{D}-x_{D}y_{B})-(x_{A}y_{D}-x_{D}y_{A})+(x_{A}y_{B}-x_{B}y_{A})|.}
Ztotožníme-li, pro jednoduchost, vrchol
A
{\displaystyle A}
A
=
(
0
,
0
)
{\displaystyle A=(0,0)}
S
=
|
x
B
y
D
−
x
D
y
B
|
.
{\displaystyle S=|x_{B}y_{D}-x_{D}y_{B}|.}
Zcela analogicky lze spočítat objem libovolného rovnoběžnostěnu , resp. nadobjem libovoného
n
{\displaystyle n}
n
{\displaystyle n}
Pokud jsou vrcholy
A
,
B
,
C
,
D
{\displaystyle A,B,C,D}
A
=
(
x
A
,
y
A
,
z
A
)
{\displaystyle A=(x_{A},y_{A},z_{A})}
B
=
(
x
B
,
y
B
,
z
B
)
{\displaystyle B=(x_{B},y_{B},z_{B})}
a
=
(
x
B
−
x
A
,
y
B
−
y
A
,
z
B
−
z
A
)
,
b
=
(
x
D
−
x
A
,
y
D
−
y
A
,
z
D
−
z
A
)
,
{\displaystyle \mathbf {a} =(x_{B}-x_{A},y_{B}-y_{A},z_{B}-z_{A}),\qquad \mathbf {b} =(x_{D}-x_{A},y_{D}-y_{A},z_{D}-z_{A}),}
je obsah rovnoběžníku roven euklidovské normě (délce) vektoru
a
×
b
{\displaystyle \mathbf {a} \times \mathbf {b} }
×
{\displaystyle \times }
vektorový součin dvou vektorů. Tedy
S
=
‖
a
×
b
‖
2
=
(
(
a
×
b
)
⋅
(
a
×
b
)
)
1
/
2
{\displaystyle S=\|\mathbf {a} \times \mathbf {b} \|_{2}={\Big (}(\mathbf {a} \times \mathbf {b} )\cdot (\mathbf {a} \times \mathbf {b} ){\Big )}^{1/2}}
kde "
⋅
{\displaystyle \,\cdot \,}
skalární součin dvou vektorů.
Pokud mají směrové vektory nulové složky ve směru osy
z
{\displaystyle z}
a
=
(
x
B
−
x
A
,
y
B
−
y
A
,
0
)
,
b
=
(
x
D
−
x
A
,
y
D
−
y
A
,
0
)
,
{\displaystyle \mathbf {a} =(x_{B}-x_{A},y_{B}-y_{A},0),\qquad \mathbf {b} =(x_{D}-x_{A},y_{D}-y_{A},0),}
pak
a
×
b
=
(
0
,
0
,
(
x
B
y
D
−
x
D
y
B
)
−
(
x
A
y
D
−
x
D
y
A
)
+
(
x
A
y
B
−
x
B
y
A
)
)
,
{\displaystyle \mathbf {a} \times \mathbf {b} ={\Big (}0,0,(x_{B}y_{D}-x_{D}y_{B})-(x_{A}y_{D}-x_{D}y_{A})+(x_{A}y_{B}-x_{B}y_{A}){\Big )},}
čímž dostaneme právě vztah pro výpočet obsahu rovnoběžníka v rovině.
Ztotožníme-li, pro jednoduchost, vrchol
A
{\displaystyle A}
A
=
(
0
,
0
,
0
)
{\displaystyle A=(0,0,0)}
a
×
b
=
(
y
B
z
D
−
y
D
z
B
,
x
D
z
B
−
x
B
z
D
,
x
B
y
D
−
x
D
y
B
)
{\displaystyle \mathbf {a} \times \mathbf {b} =(y_{B}z_{D}-y_{D}z_{B},x_{D}z_{B}-x_{B}z_{D},x_{B}y_{D}-x_{D}y_{B})}
v obecném případě, respektive
a
×
b
=
(
0
,
0
,
x
B
y
D
−
x
D
y
B
)
{\displaystyle \mathbf {a} \times \mathbf {b} =(0,0,x_{B}y_{D}-x_{D}y_{B})}
v případě, že směrové vektory mají navíc nulové složky ve směru osy
z
{\displaystyle z}
Zobecněním vektorového součinu do
n
{\displaystyle n}
(
n
−
1
)
{\displaystyle (n-1)}
n
{\displaystyle n}
(
n
−
1
)
{\displaystyle (n-1)}
n
{\displaystyle n}
Pokud je rovnoběžník dán dvěma stranovými vektory v obecném reálném
n
{\displaystyle n}
a
=
(
a
1
,
a
2
,
a
3
,
…
,
a
n
)
,
b
=
(
b
1
,
b
2
,
b
3
,
…
,
b
n
)
,
{\displaystyle \mathbf {a} =(a_{1},a_{2},a_{3},\ldots ,a_{n}),\qquad \mathbf {b} =(b_{1},b_{2},b_{3},\ldots ,b_{n}),}
pak jeho obsah je dán vztahem
S
=
‖
a
‖
2
2
‖
b
‖
2
2
−
⟨
a
,
b
⟩
2
=
(
(
a
⋅
a
)
(
b
⋅
b
)
−
(
a
⋅
b
)
2
)
1
/
2
,
{\displaystyle S={\sqrt {\|\mathbf {a} \|_{2}^{2}\|\mathbf {b} \|_{2}^{2}-\langle \mathbf {a} ,\mathbf {b} \rangle ^{2}}}={\Big (}(\mathbf {a} \cdot \mathbf {a} )(\mathbf {b} \cdot \mathbf {b} )-(\mathbf {a} \cdot \mathbf {b} )^{2}{\Big )}^{1/2},}
kde "
⟨
,
⟩
{\displaystyle \langle \,,\,\rangle }
⋅
{\displaystyle \,\cdot \,}
Dosazením
a
=
(
x
B
−
x
A
,
y
B
−
y
A
,
0
,
…
,
0
)
,
b
=
(
x
D
−
x
A
,
y
D
−
y
A
,
0
,
…
,
0
)
,
{\displaystyle \mathbf {a} =(x_{B}-x_{A},y_{B}-y_{A},0,\ldots ,0),\qquad \mathbf {b} =(x_{D}-x_{A},y_{D}-y_{A},0,\ldots ,0),}
opět dostáváme známý vztah pro obsah rovnoběžníku v rovině.
Karel Rektorys a kolektiv: Přehled užité matematiky I , Prometheus, Praha 1995, ISBN 80-85849-92-5
Marcela Palková a kolektiv: Průvodce matematikou 2 , Didaktis, Brno 2007, ISBN 978-80-7358-083-4 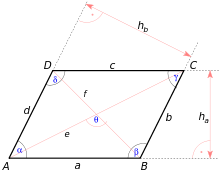
 Obrázky, zvuky či videa k tématu rovnoběžník na Wikimedia Commons
Obrázky, zvuky či videa k tématu rovnoběžník na Wikimedia Commons