Podobnost (geometrie)

Tvary se stejnou barvou si jsou podobné

Podobnost je geometrické zobrazení jednoho geometrického útvaru na jiný útvar se stejným tvarem.

Dva geometrické útvary v Euklidově prostoru jsou si podobné, pokud oba mají stejný tvar. Přesněji řečeno, jeden je shodný s útvarem, získaným jako výsledek rovnoměrného zmenšení či zvětšení druhého a jeho případné rotace, posunutí a zrcadlení.

Poměr vzdálenosti dvou bodů daného geometrického útvaru a vzdálenosti odpovídajících dvou bodů jiného geometrického útvaru (referenčního) je u podobných útvarů shodný pro každou takovou dvojici bodů a nazývá se koeficient podobnosti. Podobnost zachovává velikost úhlů a poměr délek.

Podobnost je speciálním případem afinního zobrazení. Speciálním případem podobnosti, je-li koeficient podobnosti roven 1, je shodnost.

Příkladem podobného zobrazení je stejnolehlost.

Podobnost v rovině

Pro rovinné útvary z toho vyplývá, že odpovídající hrany podobných mnohoúhelníků jsou ve vzájemném poměru a odpovídající úhly si jsou rovny.

Například všechny kružnice, čtverce a rovnostranné trojúhelníky si jsou podobné. Naopak elipsy si podobné být nemusí, stejně tak jako hyperboly.

Zpravidla se za speciální případ podobnosti považuje i shodnost, tedy podobnost s koeficientem podobnosti 1. Všechny shodné tvary jsou tedy zároveň podobné. (Některé učebnice výslovně vydělují shodné trojúhelníky z definice podobných trojúhelníků, takže musí být rozdílné nejen tvary, ale i jejich velikosti, aby se daly považovat za podobné.)

Podobné trojúhelníky

Podobné trojúhelníky jsou ty, které mají stejný tvar, ale jinou velikost. Tvar trojúhelníku je definován jeho úhly, takže dva trojúhelníky se dvěma stejnými úhly jsou podobné.

Formálně řečeno, dva trojúhelníky $\triangle ABC$ a $\triangle DEF$ jsou podobné, pokud nějaká z následujících podmínek platí:

1. Odpovídající strany mají délky ve stejném poměru, takže platí ${AB \over DE}={BC \over EF}={AC \over DF}$. Toto je to samé jako říci, že jeden trojúhelník je zvětšení druhého.

2. $\angle BAC$ je roven $\angle EDF$ , a $\angle ABC$ je roven $\angle DEF$. Toto také znamená, že $\angle ACB$ je roven $\angle DFE$.

Když jsou dva trojúhelníky $\triangle ABC$ a $\triangle DEF$ podobné, píšeme $\triangle ABC\sim \triangle DEF\,$

Podobné mnohoúhelníky

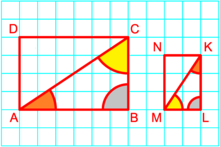
Tuto myšlenku je možné rozšířit na mnohoúhelníky s více stranami. U jakýchkoli dvou podobných mnohoúhelníků si jsou odpovídající strany přímo úměrné. Nicméně pouze úměrnost stran není dostatečná k zajištění podobnosti mnohoúhelníků kromě trojúhelníků, takže odpovídající úhly rovněž musí být shodné.

Věty o podobnosti trojúhelníků

Jsou-li trojúhelníky podobné, nám pomohou zjistit následující věty:

Věta sss - Každé dva trojúhelníky, které mají sobě rovné poměry délek všech tří dvojic odpovídajících stran, jsou si podobné.

Věta sus - Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících stran a shodují se v úhlu jimi sevřeném, jsou si podobné.

Věta usu - Každé dva trojúhelníky, které mají dva úhly stejné, si jsou podobné.

Věta ssu - Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících stran a shodují se v úhlu naproti větší straně, jsou si podobné.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Similarity (geometry) na anglické Wikipedii.

Související články

• Geometrické zobrazení
• Zobrazení

Externí odkazy

• Obrázky, zvuky či videa k tématu podobnost na Wikimedia Commons
• Slovníkové heslo podobnost ve Wikislovníku
• Encyklopedické heslo Podobnost v Ottově slovníku naučném ve Wikizdrojích