Interference
Interference (interferenční jev) znamená vzájemné ovlivňování, prolínání nebo střetávání jevů či hmoty. Nejčastěji se jedná o charakteristickou vlastnost vln. Při jejich pohybu a prolínání se v určitém bodě vzájemně zesilují, zatímco v jiných bodech vzájemně ruší. Tyto jevy se zobrazují pomocí interferenčního obrazu (interferenčního obrazce), kde je vidět střídající se projevy zesilování a zeslabování.
Interference vlnění[editovat | editovat zdroj]




Jestliže se nějakým prostředím šíří současně více vlnění z různých zdrojů, šíří se každé z vlnění tak, jako by v daném prostředí jiná vlnění neexistovala. Tato charakteristická vlastnost vlnění se nazývá principem nezávislosti šíření vlnění.
Vzhledem k principu nezávislosti šíření vlnění dochází v dané oblasti, kde se různá vlnění setkávají, k jejich skládání. Principy skládání vln jsou obdobné jako při skládání kmitů. Výsledkem skládání vln je složené vlnění. Jevy, které jsou spojeny se skládáním vlnění se označují jako interferenční jevy. Hovoří se pak o interferenci vlnění.
Výsledný kmitavý pohyb v daném místě je dán principem superpozice kmitání jednotlivých vlnění. V důsledku interference vlnění tedy dochází v některých místech ke zvýšení (zesílení) amplitudy a v některých místech k jejímu snížení (zeslabení).
Příklad a základní vlastnosti[editovat | editovat zdroj]
Určení výsledného vlnění je v obecném případě značně složitý proces, neboť skládaná vlnění se mohou odlišovat amplitudou, frekvencí, fází nebo směrem šíření. O vlastnostech interference však můžeme získat určitou představu prostřednictvím jednoduchého případu skládání dvou vlnění se stejnou frekvencí a fází nebo se stálým fázovým rozdílem. Takové vlnění se nazývá koherentní.
Uvažujme dvě koherentní vlnění s fázovým rozdílem , které se od zdrojů vlnění šíří se stejnou fázovou rychlostí ve směru osy . Vlnová délka obou vlnění je stejná, . Vzdálenost zdrojů vlnění označme . Zdroje vlnění nechť vykonávají harmonické kmity, které lze zapsat vztahy
Z těchto vztahů je vidět, že v čase procházejí body, které kmitají ve zdrojích svými rovnovážnými polohami, tzn. a .
Zvolme nyní nějaký bod ležící mimo zdroje záření, např. ve vzdálenosti od prvního zdroje a od druhého zdroje, a předpokládejme, že sledovaný bod neleží mezi zdroji vlnění. V takovém případě bude platit . Proveďme pro zjednodušení volbu bodu tak, aby platilo .
Kmity v daném bodě vyvolané zvlášť každým vlněním lze popsat vztahy
Výsledné vlnění lze získat superpozicí těchto vln, tzn.
Označíme-li vzdálenost zvoleného bodu od středu spojnice mezi zdroji jako a použijeme-li vzdálenost mezi zdroji , pak lze předchozí vztah psát jako
- ,
kde bylo pro zjednodušení zavedeno
Amplituda nezávisí na čase ani na poloze zvoleného bodu, takže je konstantou. Tato amplituda je však závislá na vzájemné vzdálenosti zdrojů vlnění. Mezní hodnoty amplitudy dostaneme, pokud položíme rovno nule nebo jedné. V závislosti na vzdálenosti zdrojů a vlnové délce může tedy amplituda A dosahovat hodnot od (tzn. vlnění nevzniká), kdy mezi vzdáleností a vlnovou délkou vlnění platí vztah pro , až po , kdy mezi vzdáleností zdrojů vlnění a vlnovou délkou platí pro .
Uvedený vztah říká, že zvolený bod koná kmity se stejnou periodou jako je perioda zdrojů a s fázovým posunem , který závisí na poloze sledovaného bodu.
Pokud sledovaný bod leží mezi zdroji, přicházejí k němu jednotlivá vlnění z opačných směrů. Výsledné vlnění lze popsat obdobně, avšak nyní má konstantní hodnotu, kdežto rozdíl se mění.
Zavedeme-li
pak lze výsledné vlnění dvou protisměrných vln zapsat ve tvaru
Uvažujme nyní případ interference dvou polarizovaných vlnění o rozdílných, ale blízkých frekvencích a , které se šíří ve stejném směru stejnou fázovou rychlostí a obě vlnění mají stejnou amplitudu. Taková vlnění lze popsat rovnicemi
Výsledné vlnění, které získáme interferencí těchto vln je
Pokud se frekvence a od sebe příliš neliší, tzn. je malá veličina, pak lze položit . Z předchozího vztahu pak dostaneme
Interferencí tedy vzniká postupná vlna s amplitudou , která se s časem mění. Ve výsledném vlnění se tedy vyskytují rázy.
Je tedy vidět, že vlnění je určitým způsobem rozděleno na skupiny (grupy) vln, které se nacházejí mezi body, v nichž je amplituda nulová. Vzdálenost mezi těmito body získáme tak, že položíme kosinus ve výrazu pro roven nule, čímž dostaneme řešení pro . Nulové body se tedy nacházejí na souřadnicích , odkud pro vzdálenost nulových bodů můžeme s využitím fázové rychlosti dostat . Tato místa však současně postupují ve směru vlnění. Vlny jsou tedy rozděleny do určitých skupin (vlnových balíků), které mají délku , a šíří se vpřed tzv. grupovou rychlostí.
Interference světla[editovat | editovat zdroj]
Pod pojem interference světla jsou zahrnovány jevy, které jsou projevem skládání světelných vln. Interference světelných vln se projevuje podobnými jevy jako interference mechanických vln, především tedy zesilováním a zeslabováním intenzity světla v různých místech. Velmi malá vlnová délka světelného vlnění však může způsobit výskyt interferenčního jevu, aniž by došlo k odklonu od přímočarého šíření světla. To umožňuje odlišovat jevy ryze interferenční, při nichž nedochází k ohybu světla, od jevů ohybových, při nichž se světlo šíří i do oblastí, které nejsou přímočarým šířením světla dostupné.
Pozorovatelný interferenční jev nastává pouze mezi koherentními vlnami. Interferují samozřejmě také vlny, jejichž fázový rozdíl se s časem mění. U světelného vlnění je vzhledem k velké frekvenci tato změna tak rychlá, že ji nelze pozorovat.
Pro popis interference světla lze využít obecných závěrů pro interferenci vlnění. Interferenci světla lze ilustrovat na několika jednoduchých příkladech.
Vznik stojatých vln při kolmém odrazu[editovat | editovat zdroj]
Pokud dopadá monochromatické světlo o vlnové délce kolmo na rovinné zrcadlo, dochází po odrazu tohoto světla ke vzniku stojatého vlnění. Při tomto jevu dochází ke skládání dvou samostatných vln, vlny dopadající a vlny odražené. Jedná se tedy o dvě proti sobě postupující vlny, které mají stejnou fázovou rychlost. Výsledné vlnění má pak charakter stojatého vlnění.
První maximum intenzity vlnění se nachází ve vzdálenosti od rovinného zrcadla. Další maxima jsou od prvního vzdáleny vždy o , kde .
Interference na planparalelní desce[editovat | editovat zdroj]
Nejčastěji lze interferenční jevy pozorovat na tenkých vrstvách, jako např. na mýdlových bublinách, kde pozorujeme různé duhové barvy, nebo podobně na tenkých vrstvách oleje na vodní hladině, na mokré dlažbě, na prasklinách v ledu apod. Obecný případ tenké vrstvy lze zjednodušit na tzv. planparalelní desku (vrstvu), což je tenká rovinná vrstva, jejíž obě strany jsou vzájemně rovnoběžné.
Při dopadu rovinné světelné vlny na planparalelní desku dochází současně k odrazu i lomu vlny, což je příčinou vzniku interference vlny.

Předpokládejme, že na planparalelní desku o indexu lomu dopadá pod úhlem rovinná vlna. Tato vlna se částečně odráží a částečně se láme do planparalelní vrstvy. Lomený paprsek se na spodním rozhraní planparalelní vrstvy opět odráží zpět, a poté se láme zpět do původního prostředí. V původním prostředí pak vzniká fázový rozdíl mezi odraženou vlnou a vlnou lomenou. Toto fázové zpoždění lze určit ze vztahu , kde je rychlost světla, je časové zpoždění mezi odraženým a lomeným paprskem, je vlnová délka a označuje dráhový rozdíl v planparalelní desce. Jako dráhový rozdíl se označuje vzdálenost, o kterou se liší vzdálenosti uražené dvěma různými paprsky. Dráhový rozdíl v planparalelní desce lze převést na dráhový rozdíl v původním prostředí pomocí vztahu , kde je relativní index lomu.
Pro dráhový rozdíl v planparalelní desce platí . Použijeme-li zákona lomu, dostaneme . Pokud označíme a , dostaneme pro dráhový rozdíl výraz
Pro určení výsledného dráhového rozdílu, je nutno ke tomuto vztahu připočíst polovinu vlnové délky vlny, tzn. . Důvodem je skutečnost, že paprsek se na hustším prostředí odráží s opačnou fází, a na prostředí řidším se stejnou fází (podobně jako při odrazu na volném a pevném konci). Výsledný dráhový rozdíl mezi dvěma paprsky má tedy hodnotu
V důsledku interference vlnění dojde k zesílení tehdy, bude-li dráhový rozdíl roven sudému počtu půlvln, tzn.
pro .
Při kolmém dopadu světla na planparalelní desku, tzn. , dojde tedy v odraženém světle k zesílení pro
a k zeslabení pro
Tyto vztahy odpovídají případu stojatých vln.
V případě světla se spojitým spektrem, lze zobecnit předchozí závěry, které byly získány pro monochromatické světlo. Výsledkem interference bílého světla na planparalelní vrstvě je světlo zbarvené v závislosti na tloušťce planparalelní vrstvy. Důvodem zabarvení světla je to, že při určité tloušťce planparalelní vrstvy se budou některé vlnové délky světla zesilovat a jiné zeslabovat, což vede ke změně spektra.

Podobné jevy lze pozorovat také při interferenci na klínové vrstvě nebo na tzv. Newtonových sklech, což je plankonvexní čočka s velkým poloměrem křivosti, která je svojí vypuklou stranou položena na rovinné skleněné destičce. Na klínové vrstvě pozorujeme v monochromatickém světle soustavu světlých a tmavých proužků, jejichž vzdálenost je závislá na velikosti klínu. Pokud světlo není monochromatické, objeví se na klínové vrstvě duhově zbarvené proužky. Podobný jev lze pozorovat také na Newtonových sklech, kde vznikají tzv. Newtonovy kroužky.
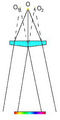
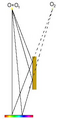
Interference světel ze dvou bodových zdrojů[editovat | editovat zdroj]
K interferenci dochází také v případě, že máme dva bodové zdroje světla, jejichž záření se v oblasti pozorování překrývá. K zajištění koherence obou zdrojů se v optice využívají soustavy zrcadel nebo hranolů, které způsobují změnu směru vlnění, které pochází z jednoho zdroje. Příkladem mohou být Fresnelova zrcadla nebo Fresnelův dvojhranol, Loydův pokus, popř. Youngův experiment.
-
Fresnelova zrcadla.
-
Fresnelův dvojhranol.
-
Loydův pokus.
Kvantová interference[editovat | editovat zdroj]
Související články[editovat | editovat zdroj]
Externí odkazy[editovat | editovat zdroj]
 Obrázky, zvuky či videa k tématu interference na Wikimedia Commons
Obrázky, zvuky či videa k tématu interference na Wikimedia Commons - http://qed.ben.cz/ - Animované interferenční obrazce

















![{\displaystyle u=u_{1}+u_{2}=A_{1}\left[\sin 2\pi \left({\frac {t}{T}}-{\frac {x_{1}}{\lambda }}\right)+\sin 2\pi \left({\frac {t}{T}}-{\frac {x_{2}}{\lambda }}\right)\right]=2A_{1}\cos {\frac {\pi (x_{2}-x_{1})}{\lambda }}\sin 2\pi \left({\frac {t}{T}}-{\frac {x_{2}+x_{1}}{2\lambda }}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d856ab42bf465786458f3adf324f5c27d4da6d2e)






















![{\displaystyle u=u_{1}+u_{2}=2A\cos 2\pi \left[{\frac {\nu -\nu ^{\prime }}{2}}\left(t-{\frac {x}{c}}\right)\right]\sin 2\pi \left[{\frac {\nu +\nu ^{\prime }}{2}}\left(t-{\frac {x}{c}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a263d168f8814534baf2588af0b9ead31de0781)