Poloměr konvergence

Poloměr konvergence mocninné řady je v matematice poloměr největšího kruhu, v němž mocninná řada konverguje. Poloměr konvergence je nezáporné reálné číslo nebo $\infty$. Je-li poloměr konvergence kladný, mocninná řada konverguje absolutně a rovnoměrně na kompaktní množině uvnitř otevřeného kruhu s poloměrem rovným poloměru konvergence a je Taylorovou řadou analytické funkce, ke které konverguje.

Definice

Pro mocninnou řadu ƒ definovanou vztahem

$f(z)=\sum _{n=0}^{\infty }c_{n}(z-a)^{n},$

kde

a je komplexní konstanta, střed kruhu konvergence,

c_n je n-tý komplexní koeficient a

z je komplexní proměnná.

je poloměr konvergence nezáporné reálné číslo r nebo $\infty$ tak, že řada konverguje, jestliže

$|z-a|<r\,$

a diverguje, jestliže

$|z-a|>r.\,$

Někdo dává přednost alternativní definici, protože existence je zjevná:

$r=\sup \left\{|z-a|\ \left|\ \sum _{n=0}^{\infty }c_{n}(z-a)^{n}\ {\text{ konverguje }}\right.\right\}$

Na hranici, tj. tam, kde |z − a| = r, může být chování mocninné řady složité a řada může pro některé hodnoty z konvergovat a pro jiné divergovat. Poloměr konvergence je nekonečný, jestliže řada konverguje pro všechna komplexní čísla z.

Hledání poloměru konvergence

Objevují se dva případy. První případ je teoretický: pokud známe všechny koeficienty $c_{n}$ pak vezmeme určité omezení a zjistíme přesný poloměr konvergence. Druhý případ je praktický: když zkonstruujeme mocninnou řadu řešení obtížného problému, typicky budeme pouze znát konečný počet členů mocninné řady, kdekoli z několika málo členů na stovky členů. V tomto druhém případě extrapolujeme graf odhady poloměr konvergence.

Teoretický poloměr

Poloměr konvergence lze nalézt aplikací Cauchyova testu na členy řady. Cauchyův test používá číslo

$C=\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|c_{n}(z-a)^{n}|}}=\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|c_{n}|}}|z-a|$

"lim sup" označuje limes superior. Cauchyův test tvrdí, že řada konverguje, jestliže C < 1 a diverguje, jestliže C > 1. Z toho plyne, že mocninná řada konverguje, jestliže vzdálenost z bodu z do středu a je menší než

$r={\frac {1}{\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|c_{n}|}}}}$

a diverguje, jestliže vzdálenost je větší než toto číslo; toto říká Cauchyova–Hadamardova věta. Přitom r = 1/0 se interpretuje jako nekonečný poloměr, což znamená, že ƒ je celá funkce.

Limitu, která se objevuje v poměrovém testu, je obvykle snazší vypočítat. Pokud tato limita existuje, znamená to, že poloměr konvergence je konečný.

$r=\lim _{n\rightarrow \infty }\left|{\frac {c_{n}}{c_{n+1}}}\right|.$

To je uvedené takto. Poměrový test říká, že řada konverguje, jestliže

$\lim _{n\to \infty }{\frac {|c_{n+1}(z-a)^{n+1}|}{|c_{n}(z-a)^{n}|}}<1.$

což je ekvivalentní s

$|z-|<{\frac {1}{\lim _{n\to \infty }{\frac {|c_{n+1}|}{|c_{n}|}}}}=\lim _{n\to \infty }\left|{\frac {c_{n}}{c_{n+1}}}\right|.$

Praktický odhad poloměru pro reálné koeficienty

Dombův–Sykesův graf funkce $f(\varepsilon )={\frac {\varepsilon (1+\varepsilon ^{3})}{\sqrt {1+2\varepsilon }}}.$ Vlevo (a) je jednoduchý graf poměru koeficientů mocninné řady $c_{n-1}/c_{n}$ jako funkce indexu $n$; vpravo, (b) je Dombův–Sykesův graf $c_{n}/c_{n-1}$ jako funkce $1/n$. Plná zelená přímka je asymptota v Dombově–Sykesově grafu, jejíž průsečík s osou y je −2 a sklon +1. Singularity tedy existují v bodě $\varepsilon =-1/2$ a proto poloměr konvergence je $r=1/2.$

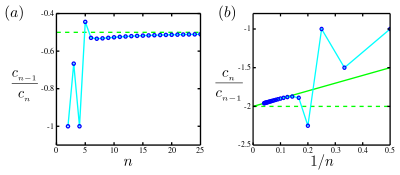
Ve vědeckých aplikacích je obvykle známý pouze konečný počet koeficientů $c_{n}$. Typicky se zvětšujícím se $n$ tyto koeficienty začnou chovat pravidelně podle toho, jak jsou ovlivňovány nejbližší singularitou omezující poloměr konvergence. Pro tento případ byly vyvinuty dvě základní techniky založené na faktu, že koeficienty Taylorovy řady jsou zhruba exponenciální funkce s poměrem $1/r$, kde r je poloměr konvergence.

• Základním případem je, když koeficienty jednoznačně mají stejné znaménko nebo pravidelně znaménka střídají. Jak již bylo ukázáno, v mnoha případech existuje limita $\lim _{n\to \infty }{{c_{n}}/{c_{n-1}}}$ a pak ${1}/{r}=\lim _{n\to \infty }{{c_{n}}/{c_{n-1}}}.$ Záporné $r$ znamená, že singularita omezující konvergenci je na záporné ose. Tuto limitu odhadneme vynesením hodnot $c_{n}/c_{n-1}$ v závislosti na $1/n$ a grafickou extrapolací na $1/n=0$ (efektivně $n=\infty$) lineárním napojením. Průsečíky s $1/n=0$ odhadují převrácené hodnoty poloměru konvergence, $1/r$. Tento graf se nazývá Dombův–Sykesův graf.
• Složitější případ nastane, pokud znaménka koeficientů mají složitější vzorek. Mercer a Roberts navrhli následující postup. Definujeme příslušnou posloupnost

$b_{n}^{2}={\frac {c_{n+1}c_{n-1}-c_{n}^{2}}{c_{n}c_{n-2}-c_{n-1}^{2}}}\quad n=3,4,5,\ldots .$

Vynesením konečně mnoha známých $b_{n}$ v závislosti na $1/n$ a grafickou extrapolací na $1/n=0$ lineárním napojením.

Průsečík s $1/n=0$ odhady převrácené hodnoty poloměru konvergence, $1/r$.

Tento postup také odhaduje dvě další charakteristiky konvergence omezující singularity. Předpokládejme, že nejbližší singularity má stupeň $p$ a má úhel $\pm \theta$ s reálnou osou. Pak sklon lineárního napojení daného výše je $-(p+1)/r$. Navíc graf ${\frac {1}{2}}\left({\frac {c_{n-1}b_{n}}{c_{n}}}+{\frac {c_{n+1}}{c_{n}b_{n}}}\right)$ v závislosti na $1/n^{2}$, pak lineární napojení extrapolované na $1/n^{2}=0$ má průsečík v $\cos \theta$.

Poloměr konvergence v komplexní analýze

Mocninnou řadu s kladným poloměrem konvergence lze považovat za holomorfní funkci, pokud bereme její argument jako komplexní proměnnou. Poloměr konvergence lze charakterizovat následující větou:

Poloměr konvergence mocninné řady ƒ se středem v bodě a se rovná vzdálenosti z a k nejbližšímu bodu, kde ƒ nelze definovat tak, aby byla holomorfní.

Množina všech bodů, jejichž vzdálenost od a je ostře menší než poloměr konvergence, se nazývá kruh konvergence.

Graf funkcí vysvětlených v textu: aproximace modře, kružnice konvergence bíle

Nejbližší bod hledáme v komplexní rovině, ne nutně na reálné ose, i kdyby střed a všechny koeficienty byly reálné. Například funkce

$f(z)={\frac {1}{1+z^{2}}}$

nemá žádné singularity na reálné ose, protože $1+z^{2}$ nemá žádné reálné kořeny. Její Taylorova řada v okolí bodu nula je

$\sum _{n=0}^{\infty }(-1)^{n}z^{2n}.$

Cauchyův test ukazuje, že poloměr konvergence je 1. V souhlase s tím má funkce ƒ(z) singularity v bodech ±i, které jsou ve vzdálenosti 1 od bodu 0.

Pro důkaz této věty viz Analyticita holomorfní funkce.

Jednoduchý příklad

Funkce arctg z trigonometrie lze rozepsat na mocninnou řadu:

$\operatorname {arctg} (z)=z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots .$

v tomto případě je snadné aplikovat Cauchyův test, z něhož plyne, že poloměr konvergence je 1.

Složitější příklad

Uvažujme tuto mocninnou řadu:

${\frac {z}{e^{z}-1}}=\sum _{n=0}^{\infty }{\frac {B_{n}}{n!}}z^{n}$

kde racionální čísla B_n jsou Bernoulliova čísla. Aplikovat poměrový test pro zjištění poloměru konvergence této řady může být obtížné. Ale výše uvedená věta komplexní analýzy problém rychle řeší. V bodě z = 0 není ve výsledku žádná singularita protože singularita je odstranitelná. Pouze neodstranitelné singularity jsou proto umístěné v jiných bodech, kde jmenovatel je nula. Řešíme

$e^{z}-1=0\,$

připomenutím, že pokud z = x + iy a e ^iy = cos(y) + i sin(y) pak

$e^{z}=e^{x}e^{iy}=e^{x}(\cos(y)+i\sin(y)),\,$

a pak vezmeme reálné x a y. Protože y je reálné, absolutní hodnota cos(y) + i sin(y) je nutně 1. Proto absolutní hodnota e ^z může být 1 pouze tehdy, když e ^x je 1; protože x je reálné, stane se to pouze pro x = 0. Proto z je ryze imaginární a cos(y) + i sin(y) = 1. Protože y je reálné, což se stane pouze, pokud cos(y) = 1 a sin(y) = 0, tak y je celé číslo větší než  $2\pi$. Následně se singulární body této funkce objeví v

z = nenulové celé číslo větší než $2\pi$i.

Singularita nejbližší bodu nula, který je středem rozvoje mocninné řady, jsou v ±$2\pi$i. Vzdálenost od středu k libovolnému z těchto bodů je $2\pi$, tak poloměr konvergence je $2\pi$.

Konvergence na hranici

Pokud mocninná řada je rozšířená v okolí bodu a a poloměr konvergence je r, pak množina všech body z tak, že Šablona:Mabs = r je kružnice nazývaný hranice kruhu konvergence. Mocninná řada může divergovat v každém bodě na hranici nebo v nějakých bodech divergovat a konvergovat v jiných bodech nebo konverguje ve všech bodech na hranici. Navíc, i kdyby řada konvergovala všude na hranici (dokonce rovnoměrně), nemusí nutně konvergovat absolutně.

Příklad 1: Mocninná řada pro funkce ƒ(z) = 1/(1 − z), rozšířená v okolí bodu z = 0, který je jednoduše

$\sum _{n=0}^{\infty }z^{n},$

má poloměr konvergence 1 a diverguje v každá bod na hranici.

Příklad 2: Mocninná řada pro g(z) = −ln(1 − z), rozšířená v okolí bodu z = 0, který je

$\sum _{n=1}^{\infty }{\frac {1}{n}}z^{n},$

má poloměr konvergence 1 a diverguje pro z = 1 ale konverguje ve všech ostatních bodech hranice. Funkce ƒ(z) z příkladu 1 je derivace funkce g(z).

Příklad 3: Mocninná řada

$\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}z^{n}$

má poloměr konvergence 1 a všude na hranici konverguje absolutně. Pokud h je funkce reprezentována touto řadou na jednotkovém kruhu, pak derivace h(z) se rovná g(z)/z s g z příkladu 2. Ukazuje se, že h(z) je dilogarithm funkce.

Příklad 4: Mocninná řada

$\sum _{i=1}^{\infty }a_{i}z^{i}{\text{ kde }}a_{i}={\frac {(-1)^{n-1}}{2^{n}n}}{\text{ pro }}n=\lfloor \log _{2}(i)\rfloor +1{\text{, jedinečná/jednoznačná celé číslo s }}2^{n-1}\leq i<2^{n},$

má poloměr konvergence 1 a konverguje rovnoměrně na celé hranici Šablona:Mabs = 1, ale nekonverguje absolutně na hranici.

Rychlost konvergence

Pokud expandujeme funkci

$f(x)=\sin x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots {\text{ pro všechny }}x$

v okolí bodu x = 0, zjistíme, že poloměr konvergence této řady je $\scriptstyle \infty$ což znamená, že tato řada konverguje pro všechna komplexní čísla. V praxi nás často zajímá přesnost numerického řešení. Jak počet členů, tak hodnota, v nichž řada je, aby byla vyčíslit ovlivňují přesnost odpovědi. Například jestliže chceme vypočítat f(0.1) = sin(0.1) s přesností na pět desítkových míst, stačí nám pouze první dva členy řady. Pokud však chceme stejnou přesnost pro x = 1, musíme vyhodnotit a sečíst prvních pět členů řady. Pro f(10), je třeba prvních 18 členů řady a pro f(100) potřebujeme vyhodnotit prvních 141 členů.

Takže pro tyto určité hodnoty je nejrychlejší konvergence rozvoje mocninné řady ve středu. Při posunutí ze středu konvergence se rychlost konvergence snižuje, dokud nedosáhne hranice (pokud hranice existuje). Po překročení hranice, bude řada divergovat.

Konvergence Dirichletovy řady v x-ové souřadnici

Podobným konceptem je konvergence Dirichletovy řady v x-ové souřadnici

$\sum _{n=1}^{\infty }{a_{n} \over n^{s}}.$

Taková řada konverguje, pokud reálná část s je větší než určité číslo závisící na koeficientech a_n: abscissa konvergence.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Radius of convergence na anglické Wikipedii.

Literatura

• BROWN, James; CHURCHILL, Ruel. Complex variables and applications. New York: McGraw-Hill, 1989. ISBN 978-0-07-010905-6. 
• STEIN, Elias; SHAKARCHI, Rami. Complex Analysis. Princeton, New Jersey: Princeton University Press, 2003. ISBN 0-691-11385-8. 

Externí odkazy

• Co je poloměr konvergence?