Strategie (teorie her)
V teorii her je strategie kompletní sada možností, které má hráč k dispozici, aby mohl hru hrát v jakékoli situaci [1]. Strategie tedy plně definuje možnosti hráčova rozhodování. Prostor strategií je seznam všech možných alternativ, které jsou hráči dostupné. Hra v normálním tvaru, je určená třemi množinami. Mimo jiné i množinou všech prostorů strategii: . Zde označuje prostor strategií i-tého hráče [2]. Strategický profil (občas nazvaný strategická kombinace) je prostor strategií pro každého hráče který plně určuje všechny akce ve hře. Profil strategie musí obsahovat pouze jednu strategii pro jednoho hráče.
Někdy dochází k záměně významu pojmu strategie a tah (anglicky move). Tah je akce vyvolaná hráčem v nějakém bodě během hry. Například v šachu je za tah považovat přesun jedné figurky podle daných pravidel (pohyb střelce z C1 na G5). Na druhou stranu strategie je soubor tahů, které tvoří komplexní způsob hraní hry na několik kol dopředu. Tah je tedy součástí strategie [3].
Pokud jsou množiny strategií jednotlivých hráčů konečné, hovoříme o konečných hrách, je-li množina strategií alespoň jednoho hráče nekonečná, jde o nekonečnou hru[3].
Prostor strategií[editovat | editovat zdroj]
Účastníci hry jsou hráči, každý hráč vybírá optimální strategii ze svého prostoru strategií podle hodnot výplatní funkce. Hráčův prostor strategií tedy definuje, jaké strategie je možné hrát. Předpokládáme, že hráči jsou inteligentní (racionální), tj. že maximalizují hodnotu své výplatní funkce. Dále předpokládáme, že hráči mají dokonalé informace, tj. že znají množiny hráčů, prostorů strategií i výplatních funkcí [2].
Například v klasické hře kámen-nůžky-papír má jeden hráč k dispozici následující prostor strategií:
- Hraju kámen
- Hraju nůžky
- Hraju papír
Každý z hráčů má tedy svou množinu přípustných řešení, kterou nazýváme prostorem strategií. Z této množiny volí hráči svoje rozhodnutí – strategii. Ukazatel, který zhodnotí důsledek volby strategie, se nazývá užitkovou funkci a hodnota tohoto ukazatele se nazývá výhra [4].
Výplatní funkce[editovat | editovat zdroj]
Pro každého hráče je definována tzv. výplatní funkce, která každé kombinaci strategií hráčů přiřadí velikost výplaty tohoto hráče. Platba neboli výplata hry je výsledek hry jednotlivých hráčů v závislosti na jimi vybraných strategiích.
Pokud uvažujeme hru hranou v normální tvaru, pak budeme rozumět trojici množin , kde je množina hráčů, je množina prostorů strategií a je množina výplatních funkcí hráčů. Každému hráči náleží strategie obsažené v příslušném . Strategie je úplný popis jak odehrát hru a každému hráči poskytuje představu o návaznosti na kroky jeho spoluhráčů. Při hraní hry v normálním tvaru si každý hráč zvolí určitou strategii a sada všech zvolených strategií (všech hráčů) dává příslušnou hodnotu výplatní funkce pro hráče Všichni hráči znají strategie své i svých spoluhráčů a znají všechny hodnoty výplatních funkcí [5].
Inteligentní hráč[editovat | editovat zdroj]
Teorie her předpokládá, že si hráč vybírá pouze efektivní strategie. Například ve hře nazvané vězňovo dilema se předpokládá, že žádný z hráčů se nechce nechat dobrovolně uvěznit. Očekává se, že hráč je konfrontován s určitým počtem situací a dokáže si je seřadit podle svých preferencí od nejvýhodnější po nejméně výhodnou. Toto seřazení musí být úplné, tj. musí pokrývat všechny situace, a tranzitivní, tj. pokud dá hráč přednost situaci A před situací B a situaci B před situací C, musí dát přednost situaci A před situací C. Na základě preferencí situací je odvozena užitková funkce (utility function) [6]. Hráč je inteligentní (racionální) pouze tehdy, pokud maximalizuje hodnotu své výplatní funkce (tj. svoji výhru) [2] . Naopak hráči, kteří se konfliktu (hry) účastní, ale výsledek hry je nezajímá, jsou nazýváni neinteligentními hráči. Tito hráči ve hře vystupují jako náhodný mechanismus, který ovlivňuje výsledky inteligentních hráčů. Často se pro neinteligentního hráče používá též termín příroda [3]. Termín Příroda navrhl John Harsanyi (1967-1968), nositel Nobelovy ceny za ekonomii. Představme si situaci s neúplnou informací, která zvyšuje nutnost uvažování názoru hráče na preference ostatních hráčů, jeho názory na názory ostatních o jeho preferencích, jeho názory o jejich názorech, o jeho názorech na jejich preference, atd. A takto se spustí cyklický systém názorů. Právě Harsanyiho teorie neúplných informací nabízí způsob doplnění struktury, ve které je informace neúplná. Hlavní principem je výpočet očekávané hodnoty. Navrhl zavést apriorní tah fiktivního hráče, nazvaného právě Příroda, který určuje typ každého hráče. Typ každého hráče a tudíž i jeho preference jsou výsledkem hodnoty náhodné proměnné, vybrané Přírodou [2]. Klasické modely teorie her považují strategie jednotlivých hráčů za ucelený souhrn jejich chování, takže jakmile hráč nějakou svoji strategii vybere, nemá možnost své jednání již korigovat [3].
Konfliktní hra[editovat | editovat zdroj]
Základním pojmem teorie her je konfliktní situace. Tímto pojmem jsou označovány všechny situace, ve kterých jde o střet zájmů účastníků konfliktu. Dosažení cíle jednotlivých účastníků je omezováno nebo korigováno cíli a zájmy ostatních [3].
Konfliktní situace může mít charakter:
- antagonistický
- neantagonistický
V případě antagonistického konfliktu dosažení cíle jedním z účastníků zamezí pozitivnímu výsledku ostatních, úspěch každého z hráčů je možný pouze na úkor úspěšnosti ostatních hráčů. Antagonistické konfliktní situace musí vyhovovat následujícím podmínkám:
- Zúčastnit se musí minimálně dva účastníci.
- Každý z účastníků rozhodovací situace zná množinu alternativ svého chování, ale také zná množinu alternativ chování svého protivníka / protivníků.
- Každý z účastníků rozhodovací situace dokáže ocenit efektivnost své volby ve všech možných případech, které by mohly nastat.
- Každý z účastníků rozhodovací situace volí z množných alternativ nezávisle na volbách protivníků [7].
Alespoň jeden účastník rozhodovací situace je inteligentní hráč, tzn. že jeho jednání je uvědomělé a volbou strategie sleduje určitý cíl. V případě neantagonistického konfliktu mají všichni účastníci možnost více či méně realizovat svoje cíle. V neantagonistickém konfliktu nejsou cíle hráčů protichůdné a hráči mohou i spolupracovat [3].
Optimální strategie[editovat | editovat zdroj]
Optimální strategie je taková strategie, od níž žádná odchylka nemůže přinést hráči výhody, za předpokladu, že druhý hráč zachová svojí optimální strategii [8]. Takto definované optimální strategie představují tzv. Nashovu rovnováhu (Nashovo rovnovážné řešení) a nazýváme je rovnovážnými strategiemi [2].
U her, které hrají dva inteligentní hráči, je poměrně snadné stanovit optimální strategii, neboť například u her s nulovým součtem (se sumou rovnou nule) je zisk jednoho hráče záporně vzatý „zisk“ druhého hráče. V případě her hraných proti přírodě však nastávají potíže [3].
Rozlišujeme dvě varianty rozhodování ve hře proti přírodě, které vznikají v antagonistickém konfliktu:
Rozhodování při riziku[editovat | editovat zdroj]
Jestliže hráč 1 zná (například na základě předchozí zkušenosti) pravděpodobnosti, s nimiž hráč 2 volí své strategie, pak se jedná o rozhodování při riziku [3].
Rozhodování při nejistotě[editovat | editovat zdroj]
Jestliže však toto rozložení pravděpodobností hráč nezná, mluvíme o rozhodování při nejistotě.
Rozhodovací principy[editovat | editovat zdroj]
V rozhodování o riziku a nejistotě využíváme Laplaceův princip. Ten navrhuje zvolit takovou strategii, která by byla optimální v případě, že by pravděpodobnosti, s nimiž nastanou různé stavy světa, byly shodné, tj. jako kdyby se jednalo o rozhodování za rizika se stejnými pravděpodobnosti přiřazenými jednotlivým stavům.
- Maximinní (pesimistické) kriterium: Tento princip navrhuje pro jednotlivé možné strategie stanovit nejnižší hodnoty užitku a zvolit takovou strategii, pro kterou je toto minimum maximální. Rozhodovatel tedy předpokládá, že se jej okolní svět bude „snažit“ co nejvíce poškodit.
- Maxmaxní (optimistické) kriterium: Tento princip navrhuje pro jednotlivé možné strategie stanovit nejvyšší hodnoty užitku a zvolit takovou strategii, pro kterou je toto maximum maximální. Rozhodovatel tedy předpokládá, že se mu okolní svět bude „snažit“ co nejvíce pomoci.
- Hurwitzovo kritérium: Jde o konvexní kombinaci optimistického a pesimistického kritéria. Vhodná volba parametru umožní nastavit vhodný kompromis mezi oběma krajnostmi – často nepřijatelné podle opatrného, resp. nepřijatelné podle důvěřivého kritéria [9].
Ryzí a smíšená strategie[editovat | editovat zdroj]
Řešením hry v případě her v maticovém stavu může být ryzí nebo smíšená strategie [10]. Jedná se o antagonistický konflikt s konečným počtem strategií.
Ryzí strategie[editovat | editovat zdroj]
Řešení hry v oboru čistých strategií znamená, že hráč dosáhne svého cíle pouze pomocí jediné své strategie. Ať se hra opakuje (má několik partií) nebo je hrána pouze jedenkrát (má jedinou partii), optimální chování hráče je dáno právě touto jedinou strategií. Ryzí optimální strategii hráče budeme značit a tato strategie přinese hráči maximální výhru, ať již hráč volí jakoukoli strategii. Ryzí optimální strategii hráče budeme značit . Je to strategie, která zaručí hráči minimální prohru, ať již hráč volí jakoukoli strategii. Pro strategie a platí:
Lze tedy říci, že jakýkoliv hráč si pohorší, pokud se odkloní od své optimální ryzí strategie. Cena hry je hodnota výplatní funkce . Pokud je cena hry nulová, jedná se o hru spravedlivou, pokud není, jedná se o hru nespravedlivou [1]. První hráč vybírá nejvyšší z nejnižších výher, kterou nazýváme dolní cena hry. Druhý hráč naopak vybírá nejmenší z nejvyšších proher, tento výsledek hry je nazýván horní cena hry. Za předpokladu rovnosti dolní a horní ceny hry je evidentní, že oba hráči nemají lepší volbu strategií. Vyberou-li své strategie jinak, bude jejich výhra menší, resp. prohra větší. Takto vybraná dvojice strategií se nazývá sedlovým bodem hry[10].
Sedlový bod[editovat | editovat zdroj]
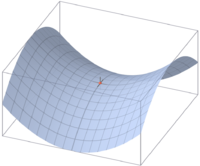
Hledáme-li optimální řešení antagonistického konfliktu hledáme vlastně stabilní řešení, stabilní v tom smyslu, že ani jednomu hráči se nevyplatí od této strategie „utéct“. Tj. má to být takové řešení, aby pokud pouze první hráč změní strategii a druhý hráč zůstane u své strategie, potom si první hráč pohorší. Stejně tak s druhým hráčem. Ze stanovení dolní ceny hry a horní ceny hry vyplývá, že optimální řešení antagonistického konfliktu (v ryzích strategiích) existuje, pokud platí:
Pokud je tato rovnost splněna, existuje prvek v matici (hra je hraná v maticovém tvaru), který je nejmenší ve svém řádku a největší ve svém sloupci. Tento prvek nazýváme sedlový bod. Obecně hra v maticovém tvaru muže mít žádný, jeden nebo více sedlových bodů. Pokud nemá žádný, neexistuje optimální ryzí strategie, pokud má jeden, určuje optimální strategii, pokud jich má více, určuje alternativní optimální (rovnovážné) strategie.[1] Maticová hra má řešení v oboru čistých strategií právě tehdy, když má sedlový bod. Z uvedené věty plyne, že řešit hru v oboru čistých strategií znamená nalézt sedlový bod hry. Odpovídající výhra, resp. prohra je cenou hry. Pokud se sedlový bod hry nepodaří nalézt, hra nemá v oboru čistých strategií řešení [10].
Smíšená strategie[editovat | editovat zdroj]
Pokud se nám nepodařilo najít sedlový prvek, znamená to, že dosavadní výklad nebyl dostatečný pro nalezení rovnovážných strategií ve všech možných rozhodovacích situacích, které je možné vyjádřit jako maticovou hru. Lze to vysvětlit na hře kámen-nůžky-papír. Tato hra je hrou dvou hráčů, z nichž každý má k dispozici tři možné strategie. Podle pravidel kámen vyhrává nad nůžkami, nůžky nad papírem a papír nad kamenem. V případě, že oba hráči zvolí stejnou strategii, nastává remíza. V reálné situaci by hráči hru opakovali, od toho však v tomto okamžiku abstrahujeme a považujeme remízu za konečný výsledek hry. Hra kámen, nůžky, papír je hrou s konstantním (nulovým) součtem, která je charakterizována maticí:
Je jednoduché si ověřit, že v této matici není možné najít sedlový prvek, takže ani není možné najít Nashovo rovnovážné řešení v ryzích strategiích. Přesto danou hru běžně dohrajeme a známe odpovídající rovnovážnou strategii, která spočívá v náhodném výběru z prostoru strategií. Pro oba hráče je rovnovážnou strategií vektor (1/3; 1/3; 1/3) kde čísla představují pravděpodobnosti, že hráč bude volit první, druhou nebo třetí strategii. Tento typ strategií nazýváme smíšenými (pravděpodobnostními) strategiemi. Také pro tyto strategie platí, že hráč, který se od rovnovážné strategie odchýlí (zvolí jiné pravděpodobnosti), nemůže nic získat, ale naopak může ztratit. Pokud maticová hra nemá řešení v ryzích strategiích, použijeme tzv. smíšeného rozšíření maticové hry. Prostory strategií nyní budou představovat vektory pravděpodobnosti, s jakou hráči zvolí jednotlivé strategie. Ryzí strategie jsou tedy zvláštním případem (podmnožinou) smíšených strategií, kdy jedna z pravděpodobností je rovna jedné, a ostatní pravděpodobnosti jsou rovny nule. Pro maticové hry platí důležitá věta. Tzv. základní věta maticových her:
- Každá maticová hra má Nashovo rovnovážné řešení ve smíšených strategiích [2].
Odkazy[editovat | editovat zdroj]
Reference[editovat | editovat zdroj]
- ↑ a b c Friebelová, Jana. Teorie her [online].[Cit. 07-12-2006].Dostupné online Archivováno 21. 2. 2007 na Wayback Machine.
- ↑ a b c d e f Dlouhý, Martin - Fiala, Petr Úvod do teorie her Oeconomica, 2007. [Cit. 01-01-2007]. ISBN 978-80-245-1273-0
- ↑ a b c d e f g h Kos, Zdeněk. Rozhodovací procesy v životním prostředí - Teorie her [online].[Cit. 21-05-2008].Dostupné online Archivováno 31. 1. 2012 na Wayback Machine.
- ↑ Daňková, Kateřina. Teorie her a její aplikace - Bakalářská práce [online].[Cit. 10-04-2008].Dostupné online Archivováno 10. 7. 2012 na Wayback Machine.
- ↑ Peliš, Michal. Teorie her jako formální teorie racionálního rozhodování [online].[Cit. 06-02-2007].Dostupné online Archivováno 13. 6. 2007 na Wayback Machine.
- ↑ Drulák, Petr. Teorie her: matematika interaktivního rozhodování [online].[Cit. 01-10-2008].Dostupné online
- ↑ Pytlíčková, Lenka. Elementy teorie her - Bakalářská práce [online].[Cit. 15-04-2008].Dostupné online[nedostupný zdroj]
- ↑ a b Roubal, Jiří. Teorie her [online].[Cit. 31-01-2006].Dostupné online[nedostupný zdroj]
- ↑ Hýkšová, Magdalena. Teorie her [online].[Cit. 21-01-2009].Dostupné online
- ↑ a b c Brožová, Helena. Rozhodovací modely a znalostní management [online].Dostupné online Archivováno 28. 2. 2009 na Wayback Machine.
Související články[editovat | editovat zdroj]
- Teorie her
- Simulace
- Kognitivní věda
- John Nash
- Equilibrium
- Souboj pohlaví
- No-win situation
- Dominantní strategie
Externí odkazy[editovat | editovat zdroj]
- (česky) Rozcestník k nalezení materiálů o teorii her [nedostupný zdroj]
- (anglicky) Podrobné informace o teorii her Archivováno 6. 12. 2009 na Wayback Machine.























