SPIHT
SPIHT (Set Partitioning in Hierarchical Trees) je kvantovací algoritmus navržený pro aplikaci na koeficienty vzniklé pyramidovým rozkladem vlnkovou transformací. V roce 1996 jej publikovali výzkumníci Amir Said a William A. Pearlman.[1] SPIHT vychází z algoritmu EZW (Embedded Zerotree Wavelet), který dále zdokonaluje.
Z praktičtějšího úhlu pohledu se jedná o algoritmus, který progresivně ukládá vlnkové koeficienty do toku bitů. Při dekódování tohoto toku se koeficienty postupně zpřesňují. Jeho práci lze tedy kdykoli přerušit a kvalita uložených koeficientů odpovídá doposud vyprodukovanému výstupu.
Algoritmus při svém postupu zohledňuje spojitost mezi koeficienty na různých úrovních rozkladu. Rozložený signál je na každé úrovni reprezentován dvojnásobným množstvím koeficientů v každém rozměru než na úrovni předchozí (směrem od kořene k listům). Vlnkové koeficienty jsou mezi sousedními měřítky (rozlišeními) silně korelovány. Lze na nich vypozorovat, že hodnota každého koeficientu bude s velkou pravděpodobností menší než hodnota jeho předchůdce. Tohoto faktu využíval již algoritmus EZW. SPIHT je sice implementačně náročnější, při stejné kvalitě však dosahuje kratšího výstupního toku bitů. Existují i různé modifikace tohoto algoritmu.
Prostorové stromy[editovat | editovat zdroj]

Algoritmus SPIHT pracuje s tzv. prostorovými stromy (spatial orientation trees). Jedná se o datovou strukturu reprezentující vlnkové koeficienty. Strom začíná kořenem. V případě jednorozměrného signálu má každý uzel dva následníky. U dvourozměrného obrazu bude mít každý uzel následníky čtyři. Listy reprezentují nejvyšší frekvence.
- Příklad
Vlnkovou transformací jednorozměrného diskrétního signálu o osmi vzorcích vznikne strom koeficientů , kde je stejnosměrná složka a s 1 ≤ ≤ 7 jsou výstupy horních propustí (dále jen AC koeficienty, indexy 4–7 značí nejvyšší frekvence). Vyjma stejnosměrné složky lze koeficienty reprezentovat stromem jako na obrázku vpravo.
V případě jednorozměrného signálu lze prostorový strom reprezentovat jako jediný vektor (tedy jednorozměrné pole koeficientů). Vektor začíná DC koeficientem (prvek s indexem 0) a následují koeficienty postupně od nejvyšší úrovně rozkladu po nejnižší. Vyjma DC koeficientu má každý prvek s indexem své dva přímé potomky na indexech až . Koeficient s indexem 1 tvoří kořen stromu. Situaci znázorňuje obrázek níže.

U transformace obrazu (tedy dvourozměrného signálu) je situace obdobná. Koeficienty zde nereprezentuje vektor ale matice (dvourozměrné pole). DC koeficient je prvek s indexy . Vyjma něj má každý prvek s indexy své čtyři přímé potomky na souřadnicích až , tedy , , a . Situaci znázorňuje obrázek níže. Tato struktura odráží vztahy mezi vlnkovými koeficienty, které vznikly pyramidovým rozkladem.
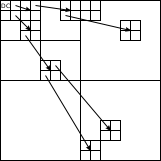
Obdobná situace nastane i u vícerozměrných signálů. Pro popis algoritmu SPIHT je ještě podstatné stanovit nad prostorovými stromy jednu operaci, resp. definovat několik množin.
První z nich je množina indexů (souřadnic) kořenů. Spadají sem koeficienty z nejvyšší úrovně rozkladu, případně též DC koeficient. Tato množina se značí (highest pyramid level). Pro dvourozměrnou variantu stromu bude tedy obsahovat indexy , , , případně .
Druhou je množina indexů přímých potomků uzlu. Značí se jako (offspring) a pro dvourozměrnou variantu stromu může být definována jako . Pořadí není podstatné, ale musí být vždy stejné.
Třetí je množina indexů všech následníků uzlu (tedy i těch nepřímých). Označuje se jako (descendant). Do této množiny tedy patří všichni přímí potomci, všichni přímí potomci přímých potomků a tak dál až k listům stromu.
Další množinou je množina indexů všech nepřímých následníku uzlu. Označuje se a spadají sem všichni následníci uzlu vyjma jeho přímých potomků. Množina je definována jako .
K efektivní implementaci práce se stromy koeficientů lze využít Mortonův rozklad. Nyní je třeba definovat operaci významnosti na množině koeficientů. Množina je významná tehdy, pokud je významný alespoň jeden její prvek. V ostatních případech je nevýznamná. Operace významnosti se značí , kde je množina indexů. Definici lze zapsat jako následující rovnici. Ke zjednodušení zápisu jednoprvkových množin lze psát jako .
Algoritmus SPIHT pracuje v jedné ze svých částí s dělením množin a používá přitom množiny právě definované. Dělení množin probíhá podle následujících dvou jednoduchých pravidel. Počáteční množina je tvořena množinami a pro všechna . První pravidlo říká, že pokud je množina všech následníků významná, je rozdělena na a čtyři samostatné prvky . Druhé pravidlo říká, že jestliže je významná množina , je tato rozdělena na čtyři množiny s .
Vlastní algoritmus[editovat | editovat zdroj]
Vlastní algoritmus pracuje se třemi seznamy. První seznam se značí LIS (list of insignificant sets), tedy seznam nevýznamných množin. Druhý se značí LIP (list of insignificant pixels) a obsahuje seznam nevýznamných koeficientů. Třetím je seznam LSP (list of significant pixels) a obsahuje seznam významných koeficientů. Seznamy LIP a LSP reprezentují jednotlivé koeficienty. Seznam LIS reprezentuje buď množinu nebo . Prvky tohoto seznamu jsou tedy dvojího typu. K jejich rozlišení je ve zmíněné práci použito následující značení – typ A reprezentuje a typ B reprezentuje .
Algoritmus pracuje iterativně a vlastní jádro sestává ze tří částí. První je průchod množinou LIP, následuje průchod množinou LIS – tyto kroky se nazývají srovnávací průchod (sorting pass). Třetí částí je průchod množinou LSP – tento krok se nazývá upřesňovací průchod (refinement pass). Při srovnávacím průchodu jsou koeficienty v LIP testovány na významnost a případně přesunuty do LSP. Obdobně jsou na významnost testovány množiny v LIS a podle uvedených pravidel případně rozděleny. Nově vzniklé množiny jsou umístěny zpět do LIS. Dělením vzniklé samostatné koeficienty jsou podle významnosti umístěny buďto do LIP nebo LSP. Jako následující algoritmus je uvedena původní varianta[1].
(Inicializace) n := ⌊log2(MAX)⌋; LSP := ϕ; LIP := ; LIS := pouze ty prvky z , které mají přímé potomky, jako prvky typu A;
(Srovnávací průchod) for each ∈ LIP do odešli ; if = 1 then přesuň do LSP a odešli znaménko ; end if end for for each ∈ LIS do (Zpracování prvku typu A) if prvek je typu A then odešli ; if = 1 then for each ∈ do odešli ; if = 1 then přidej do LSP a odešli znaménko ; end if if = 0 then přidej na konec LIP; end if end for if ≠ ϕ then přesuň na konec LIS jako prvek typu B; go to (Zpracování prvku typu B); else odeber z LIS prvek ; end if end if end if (Zpracování prvku typu B) if prvek je typu B then odešli ; if = 1 then přidej každý ∈ na konec LIS jako prvek typu A; odeber z LIS; end if end if end for
(Upřesňovací průchod) for each ∈ LSP vyjma těch prvků přidaných v posledním srovnávacím průchodu do odešli n-tý nejvýznamnější bit ; end for
(Další krok) n := n-1; go to (Srovnávací průchod);
Algoritmus pro dekódování vytvořeného bitového toku pracuje zcela shodně jako uvedený algoritmus pro kódování s tím rozdílem, že je slovo „odešli“ nahrazeno slovem „načti“. Seznamy LIS, LIP a LSP u kodéru a dekodéru musejí být tedy v každém okamžiku stejné. Dekodér postupně upřesňuje hodnoty vlnkových koeficientů. Když je koeficient přesunut do LSP, dekodér ví, že je jeho hodnota . Dekodér tedy použije tuto informaci spolu s příchozí informací o znaménku a nastaví rekonstruovaný koeficient . Podobně v průběhu upřesňovacího průchodu přičte nebo odečte dekodér od hodnotu . Nastavuje tedy odhadovanou hodnotu koeficientů do poloviny možného intervalu – je to klíčová výhoda algoritmu SPIHT.
Modifikace[editovat | editovat zdroj]
Existuje množství modifikací tohoto algoritmu. Jednou z možných úprav je předsunutí upřesňovacího průchodu před srovnávací. Tím se sníží výpočetní náročnost, protože se odbourá potřeba sledovat nově přidané prvky seznamu LSP. Jestliže jsou dále prvky seznamů procházeny vždy v pevném pořadí od kořene k poslednímu listu, zmizí skok ze zpracování uzlu typu A do zpracování uzlu typu B (v podstatě příkaz goto). LIS, LSP a LIP již pak vlastně nejsou seznamy, nýbrž množiny (které se procházejí vždy ve stejném pořadí).
Související články[editovat | editovat zdroj]
- EZW – myšlenkový předchůdce algoritmu SPIHT
- SPECK – podobný algoritmus od W. A. Pearlmana
- EBCOT – algoritmus kódování DWT použitý ve standardu JPEG 2000
Reference[editovat | editovat zdroj]
- ↑ a b Said, A.; Pearlman, W. A.: A New Fast and Efficient Image Codec Based on Set Partitioning in Hierarchical Trees. IEEE Transactions on Circuits and Systems for Video Technology, ročník 6, č. 3, Červen 1996: s. 243–250, doi:10.1109/76.499834. URL http://www.cipr.rpi.edu/research/SPIHT/EW_Code/csvt96_sp.pdf Archivováno 11. 12. 2009 na Wayback Machine.
Externí odkazy[editovat | editovat zdroj]
- (anglicky) domácí stránka algoritmu













































