Graf (teorie grafů)

Základní pojmy teorie grafů

Graf je základním objektem teorie grafů. Jedná se o reprezentaci množiny objektů, u které chceme znázornit, že některé prvky jsou propojeny. Objektům se přiřadí vrcholy a jejich propojení značí hrany mezi nimi. Grafy slouží jako abstrakce mnoha různých problémů. Často se jedná o zjednodušený model nějaké skutečné sítě (například dopravní), který zdůrazňuje topologické vlastnosti objektů (vrcholů) a zanedbává geometrické vlastnosti, například přesnou polohu.

Definice

Neorientovaný graf je dvojice $G=<V,E>$, kde V je neprázdná množina tzv. vrcholů (někdy také uzlů) a $E\subseteq \{\{u,v\}|u,v\in V,u\neq v\}$ je množina dvouprvkových množin vrcholů, tzv. (neorientovaných) hran.

Orientovaný graf je dvojice $G=<V,E>$, kde V je neprázdná množina tzv. vrcholů (uzlů) a $E\subseteq V\mathbf {x} V$ je množina uspořádaných dvojic vrcholů, tzv. (orientovaných) hran.

Hrana se tedy u neorientovaných grafů chápe jako dvouprvková množina $\{u,v\}$ vrcholů $u,v\subseteq V$. Říkáme, že hrana $\{u,v\}$ vede mezi u a v, popř. spojuje u a v. To odpovídá záměru: Graf je neorientovaný, tj. na pořadí vrcholů u hrany nezáleží.

U orientovaných grafů se hrana chápe jako uspořádaná dvojice $<u,v>$ vrcholů u a v. Pak říkáme, že hrana vede z u do v. I to odpovídá záměru: Graf je orientovaný, tj. na pořadí vrcholů u hrany záleží. Hrana $<u,v>$ je tedy něco jiného než hrana $<v,u>$. Koncové vrcholy hrany jsou u neorientované hrany $\{u,v\}$ vrcholy u a v, u orientované hrany $<u,v>$ také vrcholy u a v.

Varianty

• Někdy se v grafu hodí povolit takzvané smyčky, hrany, které začínají i končí ve stejném vrcholu. Takovému grafu se někdy říká pseudograf.
• Pokud je E multimnožina, pak se jedná o multigraf a násobným hranám se říká multihrany nebo paralelní (rovnoběžné) hrany.
• Hranám je možné určit orientaci, pak se jedná o orientovaný graf. Většinou se značí šipkou z jednoho vrcholu do druhého a říká se, že hrana e=(u,v) vede z u do v.

Zobecněním grafu takovým, že hrany nemusí obsahovat právě dva vrcholy, je hypergraf.

Okolí vrcholu

Sousedství

Pokud jsou dva vrcholy spojeny hranou, říká se, že spolu sousedí. Všechny vrcholy, se kterými daný vrchol v sousedí, jsou jeho sousedství nebo okolí N(v). $N(v)=\{u:\{v,u\}\in E\}$

Stupeň

Podrobnější informace naleznete v článku Stupeň vrcholu.

Stupeň vrcholu deg(v) je velikost jeho sousedství. V případě orientovaných grafů se rozlišuje vstupní stupeň deg⁺(v), počet hran, které vcházejí do vrcholu v, a výstupní stupeň deg⁻(v), počet hran, které vychází z vrcholu v.

$deg(v)=|\{u:\{v,u\}\in E\}|$

$deg^{+}(v)=|\{u:(u,v)\in E\}|$

$deg^{-}(v)=|\{u:(v,u)\in E\}|$

Regularita

Podrobnější informace naleznete v článku Regulární graf.

Graf je k-regulární, pokud mají všechny jeho vrcholy stupeň právě k.

Skóre

Podrobnější informace naleznete v článku Skóre grafu.

Skóre grafu je multimnožina stupňů všech vrcholů.

Princip sudosti

Platí rovnost $2|E|=\sum _{v\in V}deg(v)$, neboť každá hrana přispěje k sumě právě hodnotou 2.

Speciální stupně grafu

Často se používají hodnoty minimálního a maximálního stupně přes všechny vrcholy, minimální stupeň $\delta (G)$, maximální stupeň $\Delta (G)$ a průměrný stupeň $deg_{avg}(G)={\frac {\sum _{v\in V}deg(v)}{|V|}}={\frac {2|E|}{|V|}}$.

Podgrafy a minory

Odebrání hrany

Pokud e je hrana grafu G, G-e označuje graf na stejné množině vrcholů s množinou hran $E(G)\setminus {e}$. (graf pak neobsahuje hranu e)

Odebrání vrcholu

Pokud v je vrchol grafu G, G-v označuje graf na množině vrcholů $V(G)\setminus {v}$ a jeho množina hran se liší od původní tím, že neobsahuje hrany vrcholu v, tedy $E(G-v)=E(G)\cap {V(G)\setminus {v} \choose 2}$.

Podgraf

Podrobnější informace naleznete v článku Podgraf.

Graf G je podgraf grafu G’, pokud může vzniknout z G’ odebráním nějakých vrcholů a hran.

Indukovaný podgraf

Graf G je indukovaný podgraf grafu G’, pokud může vzniknout z G’ odebráním nějakých vrcholů.

Kontrakce hrany

Pokud e={u,v} je hrana grafu G, G.e označuje graf, který vznikne z G odstraněním e a identifikací vrcholů u a v. Pokud má vzniknout obyčejný graf, požaduje se odstranění násobných hran a smyček, které mohly vzniknout.

Minor

Podrobnější informace naleznete v článku Minor (teorie grafů).

Graf G je minor grafu G’, pokud může vzniknout z G’ odebráním nějakých vrcholů a hran a kontrakcí hran.

Sledy, tahy, cesty

Sled

Podrobnější informace naleznete v článku Sled (graf).

Sled v grafu je posloupnost vrcholů taková, že mezi každými dvěma po sobě jdoucími je hrana.

Tah

Podrobnější informace naleznete v článku Tah (graf).

Tah v grafu je sled, ve kterém se neopakují hrany.

Cesta

Podrobnější informace naleznete v článku Cesta (graf).

Cesta je sled, ve kterém se neopakují vrcholy, tedy každý vrchol se v cestě objevuje nejvýše jednou. Existuje-li mezi dvěma vrcholy sled v grafu, existuje mezi nimi i cesta (protože každý úsek mezi dvěma výskyty stejného vrcholu se dá „vystřihnout“).

Na všechny tyto pojmy se dá také nahlížet jako na podgraf.

Souvislost

Graf je souvislý, pokud mezi každými dvěma vrcholy existuje cesta. V případě orientovaných grafů se mluví o silné souvislosti, pokud mezi každými dvěma vrcholy v obou směrech existuje cesta respektující orientaci.

Komponenta souvislosti

Podrobnější informace naleznete v článku Komponenta grafu.

Komponenta souvislosti je každý v inkluzi maximální souvislý podgraf. Souvislé grafy jsou právě ty, co mají pouze jednu komponentu souvislosti. U orientovaných grafů se navíc rozlišují silně souvislé komponenty.

Důležité typy grafů

• Strom
• Cesta
• Kružnice
• Úplný graf
• Bipartitní graf

Reprezentace grafu

• „obrázkem“, správně řečeno nakreslením: viz rovinný graf
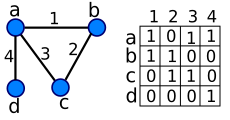
• maticí sousednosti: je-li |V| = n, pak čtvercová matice sousednosti A je typu $\{0,1\}^{n\times n}$ a platí ${\mathit {A}}_{i,j}=1\Leftrightarrow \{i,j\}\in {\mathit {E}}$. Pokud je graf neorientovaný, stačí na jeho reprezentaci (horní nebo dolní) trojúhejníková matice.
• maticí vzdálenosti: jsou-li hrany grafu ohodnocené, lze výše uvedenou matici modifikovat tak, že místo jedničky je na daném pozici uvedeno ohodnocení (délka) příslušné hrany
• Laplaceovou maticí: opět čtvercová matice, tentokrát typu $\mathbb {Z} ^{n\times n}$, pro niž platí

$({\mathit {L}}_{G})_{i,j}={\begin{cases}deg(i),&i=j\\-1,&\{i,j\}\in {\mathit {E}}\\0,&i\neq j\;\land \{i,j\}\notin {\mathit {E}}\end{cases}}$

• maticí incidence: je-li |V| = n a |E| = m, pak matice incidence je typu $\{-1,0,+1\}^{n\times m}$ a platí

$({\mathit {I}}_{G})_{i,e}={\begin{cases}-1,&e=(i,\bullet )\\+1,&e=(\bullet ,i)\\0,&{\mbox{jinak}}\end{cases}}$

Jinými slovy, každá hrana má 1 u vrcholu kde začíná a -1 u vrcholu kde končí. U neorientovaných grafů je vždy +1 když je hrana v incidenci s vrcholem.

Pro neorientovaný graf: Pro orientovaný graf:

• seznamem sousedů: je-li |V| = n, uspořádáme vrcholy grafu do pole velikosti n a v i-tém prvku tohoto pole bude ukazatel na spojový seznam vrcholů, které s vrcholem i sousedí. Toto uspořádání je vhodné při množství údajů menším než n^2. Tj. při ostře menším počtu hran než n^2, kde n je počet vrcholů. Jedná se o tzv. řídké grafy, kterých je v prostředí sítí nejvíce.

Isomorfismus grafů

Grafy G a G’ jsou isomorfní právě tehdy, když existuje taková bijekce $f:V(G)\to V(G')$, že platí $\{{\mathit {i,j}}\}\in E(G)\Leftrightarrow \{{\mathit {f(i),f(j)}}\}\in E(G')$. Tedy zhruba řečeno, G a G' se liší pouze „očíslováním“ svých vrcholů.

Ohodnocení grafu

Pro některé účely se vrcholy nebo hrany grafu ohodnocují, například reálnými čísly, pomocí ohodnocovací funkce $w:E\rightarrow \mathbb {R}$ nebo $V\rightarrow \mathbb {R}$.

Reference

• Jiří Matoušek, Jaroslav Nešetřil: Kapitoly z diskrétní matematiky, nakladatelství Karolinum, Praha 2002, ISBN 80-246-0084-6
• Roman Čada, Tomáš Kaiser, Zdeněk Ryjáček: Diskrétní matematika, Západočeská univerzita v Plzni, Březen 2004, ISBN 80-7082-939-7
• Zdeněk Ryjáček: Pracovní texty přednášek Teorie grafů a diskrétní optimalizace 1 Volně ke stažení, PDF verze
• prof. RNDr. Radim Bělohlávek, DSc.: Algoritmická matematika 2 Volně ke stažení, PDF verze

• Jiří Demel: Grafy a jejich aplikace, nakladatelství Academia, Praha 2002, ISBN 80-200-0990-6

Autoritní data	MA: 132525143