Věta o homomorfismu

Věta o homomorfismu, někdy také nazývaná první věta o izomorfismu, je v teorii grup a v abstraktní algebře věta, která ukazuje souvislost struktury dvou objektů, mezi kterými existuje homomorfismus, a jádrem a obrazem homomorfismu.

Věta o homomorfismu se používá pro matematický důkaz vět o izomorfismu.

Verze pro grupy

Znázornění věty o homomorfismu, kde f je homomorfismus, N je normální podgrupa grupy G a e je neutrální prvek grupy G.

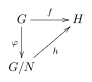
Jsou dány dvě grupy G a H a grupový homomorfismus f : G → H. Nechť N je normální podgrupa v G a φ přirozený surjektivní homomorfismus G → G / N (kde G / N je faktorová grupa grupy G podle N). Pokud N je podmnožina jádra ker(f), pak existuje jediný homomorfismus h : G / N → H takový, že f = h ∘ φ.

Jinými slovy přirozená projekce φ je univerzální mezi homomorfismy na G, které zobrazují N na neutrální prvek.

Situace je popsaná následujícím komutativním diagramem:

h je injektivní právě tehdy, když N = ker(f). Pokud tedy položíme N = ker(f), okamžitě dostáváme první větu o izomorfismu.

Větu o homomorfismu grup lze stručně formulovat takto: „Každý homomorfní obraz grupy je izomorfní s faktorovou grupou“.

Důkaz

Důkaz vyplývá ze dvou základních faktů o homomorfismech, jmenovitě o zachování grupové operace, a zobrazení neutrálního prvku na neutrální prvek. Potřebujeme ukázat, že pokud $\phi :G\to H$ je homomorfismus grup, pak:

1. ${\text{im}}(\phi )$ je podgrupa grupy $H$.
2. $G/\ker(\phi )$ je izomorfní s ${\text{im}}(\phi )$.

Důkaz bodu 1

Operace, kterou $\phi$ zachovává, je grupová operace. Pokud $a,b\in {\text{im}}(\phi )$, pak existují prvky $a',b'\in G$ takové, že $\phi (a')=a$ a $\phi (b')=b$. Pro tyto $a$ a $b$, máme $ab=\phi (a')\phi (b')=\phi (a'b')\in {\text{im}}(\phi )$ (protože $\phi$ zachovává grupové operace), a tedy, uzávěrová vlastnost je splněna v ${\text{im}}(\phi )$. Neutrální prvek $e\in H$ je také v ${\text{im}}(\phi )$, protože $\phi$ převádí neutrální prvek grupy $G$ to to. Protože ke každému prvku $a'$ v $G$ má inverzní $(a')^{-1}$ takový, že $\phi ((a')^{-1})=(\phi (a'))^{-1}$ (protože $\phi$ zachovává inverzní vlastnost také), máme inverzní pro každý prvek $\phi (a')=a$ v ${\text{im}}(\phi )$, proto, ${\text{im}}(\phi )$ je podgrupa grupy $H$.

Důkaz bodu 2

Zkonstruujeme zobrazení $\psi :G/\ker(\phi )\to {\text{im}}(\phi )$ by $\psi (a\ker(\phi ))=\phi (a)$. Toto zobrazení je definované korektně, protože pokud $a\ker(\phi )=b\ker(\phi )$, pak $b^{-1}a\in \ker(\phi )$ a tedy $\phi (b^{-1}a)=e\Rightarrow \phi (b^{-1})\phi (a)=e$ což dává $\phi (a)=\phi (b)$. Toto zobrazení je izomorfismus. Z definice je vidět, že $\psi$ je surjektivní na ${\text{im}}(\phi )$. Pro důkaz injektivity je třeba si uvědomit, že pokud $\psi (a\ker(\phi ))=\psi (b\ker(\phi ))$, pak $\phi (a)=\phi (b)$, což implikuje $b^{-1}a\in \ker(\phi ),$ takže $a\ker(\phi )=b\ker(\phi )$. Nakonec

$\psi ((a\ker(\phi ))(b\ker(\phi )))=\psi (ab\ker(\phi ))=\phi (ab)=\phi (a)\phi (b)=\psi (a\ker(\phi ))\psi (b\ker(\phi )),$

tedy $\psi$ zachovává grupové operace. Tedy $\psi$ je izomorfismus mezi $G/\ker(\phi )$ a ${\text{im}}(\phi )$, což uzavírá důkaz.

Aplikace

Grupově-teoretickou verzi věty o homomorfismu lze použít pro důkaz, že určité dvě grupy jsou izomorfní. Dva příklady jsou uvedené níže.

Celá čísla modulo n

Pro každý $n\in \mathbb {N}$, uvažujme grupy $\mathbb {Z}$ a $\mathbb {Z} _{n}$ a grupový homomorfismus $f:\mathbb {Z} \rightarrow \mathbb {Z} _{n}$ definovaný vztahem $m\mapsto m{\text{ mod }}n$ (viz Modulární aritmetika). Dále uvažujme jádro homomorfismu $f$, ${\text{ker}}(f)=n\mathbb {Z}$, které je normální podgrupou v $\mathbb {Z}$. Existuje přirozený surjektivní homomorfismus $\varphi :\mathbb {Z} \rightarrow \mathbb {Z} /n\mathbb {Z}$ definovaný vztahem $m\mapsto m+n\mathbb {Z}$. Věta tvrdí, že existuje izomorfismus $h$ mezi $\mathbb {Z} _{n}$ a $\mathbb {Z} /n\mathbb {Z}$ nebo jinými slovy $\mathbb {Z} _{n}\cong \mathbb {Z} /n\mathbb {Z}$. Situace je znázorněna následujícím komutativním diagramem:

N/C věta

Nechť $G$ je grupa s podgrupou $H$. Nechť $C_{G}(H)$, $N_{G}(H)$ a ${\text{Aut}}(H)$ je po řadě centralizátor, normalizátor a grupa automorfismů grupy $H$ v $G$. Potom věta N/C říká, že $N_{G}(H)/C_{G}(H)$ je izomorfní s podgrupou ${\text{Aut}}(H)$.

Důkaz

Jsme schopni najít grupový homomorfismus $f:N_{G}(H)\rightarrow {\text{Aut}}(H)$ definovaný vztahem $g\mapsto ghg^{-1}$, pro všechna $h\in H$. Jádro homomorfismu $f$ je zřejmě $C_{G}(H)$. Máme tedy přirozený surjektivní homomorfismus $\varphi :N_{G}(H)\rightarrow N_{G}(H)/C_{G}(H)$ definovaný vztahem $g\mapsto gC(H)$. Věta o homomorfismu pak tvrdí, že existuje izomorfismus mezi $N_{G}(H)/C_{G}(H)$ a $\varphi (N_{G}(H))$, který je podgrupou grupy ${\text{Aut}}(H)$.

Jiné verze

Podobné věty platí pro monoidy, vektorové prostory, moduly a okruhy.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Fundamental theorem on homomorphisms na anglické Wikipedii.

Literatura

• BEACHY, John A., 1999. Introductory Lectures on Rings and Modules. [s.l.]: Cambridge University Press. (London Mathematical Society Student Texts). Dostupné online. ISBN 9780521644075. S. 27. 
• GROVE, Larry C., 2012. Algebra. [s.l.]: Courier Corporation. (Dover Books on Mathematics). Dostupné online. ISBN 9780486142135. S. 11. 
• JACOBSON, Nathan, 2012. Basic Algebra II. 2. vyd. [s.l.]: Courier Corporation. (Dover Books on Mathematics). Dostupné online. ISBN 9780486135212. S. 62. 
• ROSE, John S., 1994. A course on Group Theory [reprint of the 1978 original]. [s.l.]: Dover Publications, Inc., New York. Dostupné online. ISBN 0-486-68194-7. S. 44–45. 
• MAC LANE, Saunders; BIRKHOFF, Garrett, 1973. Algebra. Bratislava: Alfa, vydavateľstvo technickej a ekonomickej literatúry. (slovensky) 
• Studijní text katedry algebry MFF UK [online]. [cit. 2024-09-19]. Dostupné online. 

Související články

• Faktorová kategorie