Malfattiho kruhy

Malfattiho kruhy (anglicky Malfatti's circles), někdy též nazýváno jako Malfattiho problém je úloha kterou r. 1803 formuloval italský matematik Gian Francesco Malffati.
Formulace problému a řešení[editovat | editovat zdroj]
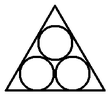
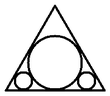
Úkolem je vepsat do daného trojúhelníku tři nepřekrývající se kruhy tak, aby jejich celkový obsah byl maximální. Sám Malfatti se domníval že zná správné řešení: nakreslit kruhy tak, aby se každý dotýkal dvou stran trojúhelníku a obou zbývajících kruhů (viz obrázek Malfattiho kruhy). Malffatiho řešení však nebylo správné, přestože se více než sto let věřilo, že ano. Roku 1930 však bylo zjištěno že u rovnostranných trojúhelníků toto pravidlo neplatí, zde je zapotřebí nakreslit nejprve kruh co největší možný a poté dokreslit dva menší. Obsahy kruhů zabírají části z celkových ploch trojúhelníků které jsou dány zlomky:
Jak je z horních vztahů vidno, zlomek vlevo má o něco menší hodnotu nežli zlomek vpravo.
Obzvláště očividně odhalil neplatnost Malfattiho řešení v roce 1967 Hovard Eves u dlouhých a úzkých trojúhelníků. Dle Malfattiho by bylo správně vepsat trojúhelníky jak je znázorněno na obrázku dole vlevo, nicméně je zcela evidentní že plocha zabraná kruhy na dolním pravém obrázku je větší.
Roku 1967 dokázal Michael Goldberg že Malfattiho pravidlo není správné nikdy, bez ohledu na tvar trojúhelníku. Roku 1990 matematik Ogilvi a v roce 1991 Wells ukázali případy kdy se správně musí jeden kruh dotýkat všech stran trojúhelníka. A konečně kompletní řešení problému představil v roce 1992 ruský matematik V. A. Zalgaller.
Odkazy[editovat | editovat zdroj]
Literatura[editovat | editovat zdroj]
- Acheson, David "1089 a další parádní čísla, Matematická dobrodružství" (1089 & All That : A Journey into Mathematics)
- Goldberg, M. "On the Original Malfatti Problem." Math. Mag. 40, 241-247, 1967.
Externí odkazy[editovat | editovat zdroj]
 Obrázky, zvuky či videa k tématu Malfattiho kruhy na Wikimedia Commons
Obrázky, zvuky či videa k tématu Malfattiho kruhy na Wikimedia Commons - Malfatti's Problem