Kvadratická rovnice

Jako kvadratická rovnice se v matematice označuje algebraická rovnice druhého stupně, tzn. rovnice o jedné neznámé, ve které neznámá vystupuje ve druhé mocnině (x²). V základním tvaru vypadá následovně:

$ax^{2}+bx+c=0$

Zde jsou a, b, c nějaká reálná čísla, tzv. koeficienty této rovnice, x je neznámá. Koeficient a je vždy různý od nuly, neboť pro a = 0 se jedná o lineární rovnici. Často se kvadratická rovnice vyjadřuje v základním (normovaném) tvaru, kde a = 1. Do tohoto tvaru lze převést každou kvadratickou rovnici jejím vydělením koeficientem a.

Jednotlivé členy mají také svá pojmenování: ax² je kvadratický člen, bx je lineární člen a c absolutní člen.

Řešení rovnice

Při řešení rovnice se nejprve vypočítá tzv. diskriminant $D=b^{2}-4ac$. Podle jeho hodnoty pak mohou nastat tři případy:

• D = 0, tehdy má rovnice jedno (tzv. dvojnásobné) řešení $x={\frac {-b}{2a}}$. Původní rovnici je možno zapsat ve tvaru $a(x+{\frac {b}{2a}})^{2}=0$.
• D > 0, tehdy má rovnice dvě různá reálná řešení $x_{1,2}={\frac {-b\pm {\sqrt {D}}}{2a}}$. Rovnici je možno zapsat ve tvaru $a(x-x_{1})(x-x_{2})=0$.
• D < 0, tehdy rovnice nemá v reálném oboru řešení. Jejím řešením jsou dvě komplexně sdružená čísla $x_{1,2}={\frac {-b\pm i{\sqrt {-D}}}{2a}}$. Rovnici je opět možné napsat ve tvaru $a(x-x_{1})(x-x_{2})=0$, ovšem kořeny x_1,2 jsou nyní komplexní čísla.

Příklad

• $2x^{2}+9x+4=0$
• $D=b^{2}-4ac=9^{2}-4\cdot 2\cdot 4=49$
• $x_{1,2}={\frac {-9\pm {\sqrt {49}}}{2\cdot 2}}$
• $x_{1}={\frac {-9+7}{4}}=-{\frac {1}{2}},x_{2}={\frac {-9-7}{4}}=-4$

Odvození

Vzorce pro výpočet diskriminantu a kořenů lze odvodit následujícím způsobem:

Vychází se z obecného tvaru rovnice:

$ax^{2}+bx+c=0$ .

Protože a≠0, lze jím rovnici vynásobit:

$a^{2}x^{2}+abx+ac=0$ ,  což lze doplnit na druhou mocninu dvojčlenu:

$(ax)^{2}+2ax{\frac {b}{2}}+\left({\frac {b}{2}}\right)^{2}-\left({\frac {b}{2}}\right)^{2}+ac=0$;  nyní se zapíše vzniklý trojčlen jako druhá mocnina:

$\left(ax+{\frac {b}{2}}\right)^{2}-{\frac {b^{2}}{4}}+ac=0$   a rovnice se vynásobí čtyřmi:

$4\left(ax+{\frac {b}{2}}\right)^{2}-b^{2}+4ac=0$;  první člen se roznásobí, z druhého vytkne číslo -1

$(2ax+b)^{2}-(b^{2}-4ac)=0$   a převede se na pravou stranu:

$(2ax+b)^{2}=b^{2}-4ac$.

Pravá je diskriminant, jehož nezápornost umožní odmocnění obou stran rovnice (v reálných číslech). Odtud plyne, proč hodnota diskriminantu určuje počet řešení kvadratické rovnice. Po odmocnění (které dává při kladném diskriminantu dvě hodnoty lišící se znaménkem, proto jsou i na levé straně uvedeny dva kořeny):

$2ax_{1,2}+b=\pm {\sqrt {b^{2}-4ac}}=0$,  po odečtení b od obou stran:

$2ax_{1,2}=-b\pm {\sqrt {b^{2}-4ac}}=0$  a vydělením rovnice nenulovým výrazem 2a se dostane vzorec pro kořeny rovnice:

$x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\,$.

Komplexní koeficienty

V nejobecnějším případě jsou také koeficienty $a,b,c$ komplexní čísla. Řešení získáme opět výpočtem diskriminantu $D=b^{2}-4ac$ a jeho druhé odmocniny v oboru komplexních čísel. Vzorec řešení je stejný jako v případě reálných koeficientů. $x_{1,2}={\frac {-b\pm {\sqrt {D}}}{2a}}$. Výsledkem jsou obecně dvě komplexní čísla, mezi nimiž nemusí být žádný vztah. Rovnici je opět možné napsat ve tvaru $a(x-x_{1})(x-x_{2})=0$. V případě nulového diskriminantu obě řešení splývají v jedno komplexní číslo $x_{0}$ a rovnice má tvar $a(x-x_{0})^{2}=0$.

Další rovnosti

Pro kořeny rovnice platí následující rovnosti (jedná se o speciální případ tzv. Vièteho vztahů):

• $x_{1}+x_{2}=-{\frac {b}{a}}$
• $x_{1}x_{2}={\frac {c}{a}}$

Geometrický význam

Levá strana rovnice (ax² + bx + c) popisuje parabolu s osou rovnoběžnou s osou y. Pokud je a>0, je parabola otevřená směrem nahoru (má vrchol dole), při a<0 je otevřená dolů (vrchol je nahoře). Řešení kvadratické rovnice odpovídá hledání průsečíků této paraboly s osou x (pravá strana z rovnice dělá výraz y=0). Podle polohy paraboly mohou nastat tři případy:

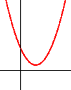
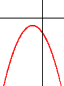
• Parabola leží celá nad (pro a>0) nebo celá pod (pro a<0) osou x. To nastane v případě, že D<0. Tehdy parabola nemá žádný průsečík s osou x, což znamená, že kvadratická rovnice nemá v reálných číslech řešení. Kořeny rovnice jsou 2 komplexně sdružená komplexní čísla.
• Vrchol paraboly leží právě na ose x. To nastane v případě, že D=0. Tehdy se parabola osy x dotýká, tzn. má s ní jeden společný bod (právě vrchol paraboly), tzn. kvadratická rovnice má jedno řešení.
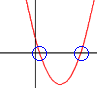
• V ostatních případech osa x parabolu protíná ve dvou bodech. To nastane v případě, že D>0. Tehdy existují dva průsečíky osy x s parabolou, tzn. rovnice má dvě různá řešení.

• 
  x² − x + 1: Celá parabola je nad osou x.
• 
  −x² − 2x − 2: Celá parabola je pod osou x.
• 
  −x² + 2x − 1: Parabola se dotýká osy x.
• 
  x² − 5x + 2: Osa x parabolu protíná.

Související články

• Parabola
• Lineární rovnice
• Kubická rovnice
• Kvartická rovnice
• Binomická rovnice

Externí odkazy

• Obrázky, zvuky či videa k tématu kvadratická rovnice na Wikimedia Commons
• Kvadratická rovnice v matematické encyklopedii MathWorld (anglicky)

Autoritní data	PSH: 7219 BNF: cb12124598x (data) LCCN: sh85044517 NLI: 987007552898205171