Rovinný graf

Rovinný graf (též planární graf) je graf, pro který existuje takové rovinné nakreslení, že se žádné dvě hrany nekříží.

Rovinné nakreslení

Oblouk je podmnožina roviny tvaru $\sigma(\langle 0,1 \rangle)$, kde $\sigma: [0, 1] \rightarrow \mathbb{R}^2$ je nějaké spojité a prosté (až na koncové body) zobrazení intervalu $\langle 0, 1 \rangle$ do roviny. Body $\sigma(0)$ a $\sigma(1)$ se nazývají koncové body oblouku.

Rovinné nakreslení je pak zobrazení $b$, které každému vrcholu $v$ přiřazuje bod roviny $b(v)$ a hraně ${i, j}$ přiřadí oblouk s koncovými body $\sigma(i)$ a $\sigma(j)$. Zobrazení je prosté (různým vrcholům odpovídají různé body roviny) a žádný bod $b(v)$ není nekoncovým bodem žádného oblouku. Graf spolu s takovýmto zobrazením nazveme topologický graf.

Topologický graf je rovinný, pokud libovolné dva oblouky odpovídající hranám $e$ a $f$ ($e \ne f$) mají společné nejvýše koncové body.

Stěna grafu

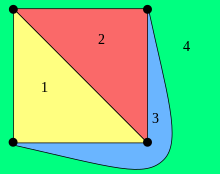
Nechť $A\subseteq\mathbb{R}^2$ je nějaká podmnožina roviny. Nazveme ji souvislou, pokud pro $\forall x, y \in A$ platí, že existuje oblouk $o$ s koncovými body $x$ a $y$ takový, že $o\subseteq A$. Oblouky příslušné hranám nějakého topologického grafu pak podle této relace souvislosti rozdělují rovinu na třídy ekvivalence, které se nazývají stěny grafu.

Charakterizace rovinných grafů

Kuratowského věta

Graf G je rovinný právě tehdy, není-li žádný jeho podgraf izomorfní dělení grafu $K_5$ ani $K_{3, 3}$. ($K_5$ označuje úplný graf na pěti vrcholech, $K_{3, 3}$ pak úplný bipartitní graf.)

K₄, úplný graf na 4 vrcholech, lze zakreslit do roviny bez křížení hran. Pro K₅ to možné není.

Eulerův vzorec

Pro rovinné grafy také platí následující vzorec, je to ovšem pouze implikace: Je-li $G = (V, E)$ souvislý rovinný graf, pak $|V| - |E| + s = 2$, kde $s$ je počet stěn nějakého rovinného nakreslení tohoto grafu.

Příklad ukazuje graf K₄ se 4 vrcholy, 6 hranami a vyznačenými 4 stěnami. Eulerův vztah platí, 4 − 6 + 4 = 2.

Maximální počet hran

Je-li $G = (V, E)$ rovinný graf, pak platí, že $|E|\le 3|V| - 6$. Neobsahuje-li navíc tento graf jako podgraf trojúhelník (tj. $K_3$, úplný graf na 3 vrcholech), pak $|E|\le 2|V| - 4$.

Z prvního tvrzení vyplývá důležitý fakt, a to, že každý rovinný graf má alespoň jeden vrchol stupně nejvýše 5.

Související články

• Duální graf
• Barvení grafu