Riemannova hypotéza
Riemannova hypotéza (také Riemannova zeta-hypotéza) je jeden z nejslavnějších a nejdůležitějších nevyřešených problémů současné matematiky. Poprvé byla formulována německým matematikem Bernhardem Riemannem v roce 1859. Dokázáním Riemannovy hypotézy by bylo vyřešeno velké množství hlubokých problémů z různých oblastí matematiky (zejména teorie čísel), nejen proto byla v roce 2000 zařazena mezi 7 nejdůležitějších nevyřešených matematických problémů nového tisíciletí (tzv. problémy tisíciletí).
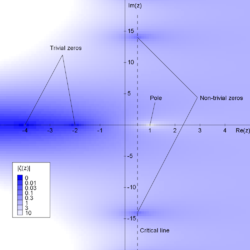
Riemannova hypotéza je domněnka o rozložení kořenů tzv. Riemannovy zeta-funkce definované v celé komplexní rovině kromě bodu 1. Tato funkce má některé ze svých kořenů, tzv. triviální nulové body, v sudých záporných celých číslech. Kromě těchto kořenů existují ještě další, které se nazývají netriviální nulové body. Riemannova hypotéza je tvrzení:
- Všechny netriviální nulové body Riemannovy zeta-funkce mají reálnou část rovnu 1/2.
Čísla, jejichž reálná část je rovna 1/2, tvoří v komplexní rovině přímku, která se nazývá kritická přímka.
Nejsilnějšími známými částečnými řešeními Riemannovy hypotézy jsou různé verze věty o kritické přímce, které říkají, že na kritické přímce se vyskytuje „hodně“ netriviálních nulových bodů.
Netriviální nulové body
V roce 1900 byla s matematickou jistotou známa následující fakta o umístění netriviálních nulových bodů v komplexní rovině:
- Je jich nekonečně mnoho a všechny mají reálnou část mezi 0 a 1, přičemž krajní body vylučujeme.
Použijeme-li komplexní rovinu ke znázornění této situace, můžeme říci, že víme, že všechny netriviální nulové body leží v kritickém pásu. Riemannova hypotéza je však daleko silnější tvrzení - totiž že všechny leží na kritické přímce.
- Nulové body se objevují v komplexně sdružených dvojicích.
Jinými slovy, je-li nulový bod, je i nulový bod.
- Jejich reálné části jsou symetrické podle kritické přímky.
Tedy jestliže existuje nějaký nulový bod mimo kritickou přímku, pak jeho zrcadlový obraz podle kritické přímky je také nulovým bodem.
Odkazy
Související články
Literatura
- John Derbyshire, Posedlost prvočísly, (2007) Academia, - Počet stran: 407.
- Bernhard Riemann, Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse, (1859) Monatsberichte der Berliner Akademie.
- Jacques Hadamard, Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques, Bulletin Société Mathématique de France 14 (1896) pp 199-220.
Externí odkazy
- Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse – původní Riemannův článek, v němž formuluje Riemannovu hypotézu (anglicky) (německy)



