Rolleova věta

Geometrický význam Rolleovy věty.

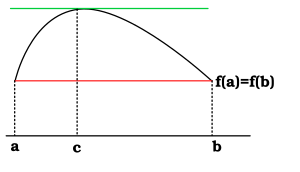
Rolleova věta (též Rollova věta) je matematická věta diferenciálního počtu.

Věta

Nechť f je spojitá funkce na uzavřeném intervalu $\left[a,b\right]$ a nechť pro každý bod x otevřeného intervalu $\left(a,b\right)$ existuje derivace $f'\left(x\right)$ a nechť $f\left(a\right) = f\left(b\right)$. Pak existuje bod c v otevřeném intervalu $\left(a,b\right)$, pro nějž platí

$f'\left(c\right) = 0$.

Důkaz

• Nechť funkce f je konstantní. Potom derivace $f'\left(x\right)=0, \forall x \in \left(a,b\right)$ a věta je dokázána.
• Nechť funkce f není konstantní. Jelikož $f\left(a\right) = f\left(b\right)$ a funkce není konstantní, musí existovat $d \in \left(a,b\right)$ takové, že $f\left(d\right) > f\left(a\right) = f\left(b\right)$ nebo $f\left(d\right) < f\left(a\right) = f\left(b\right)$. Předpokládejme, že $f\left(d\right) > f\left(a\right) = f\left(b\right)$.

Využijeme věty tvrdící, že každá funkce spojitá na uzavřeném intervalu $\left[a,b\right]$ nabývá na tomto intervalu svého maxima i minima a zabývejme se maximem. Jelikož existuje $d \in \left(a,b\right)$ takové, že $f\left(d\right) > f\left(a\right) = f\left(b\right)$, tak maximum nemůže ležet ani v a, ani v b. Leží tedy uvnitř intervalu, v bodě c. Z věty o nutné podmínce lokálního extrému vyplývá, že tedy v bodě c, kde se nalézá lokální extrém funkce, $f'\left(c\right) = 0$.

Analogické tvrzení platí i pro minimum.

Související články

• Věta o střední hodnotě diferenciálního počtu
• Cauchyova věta o střední hodnotě