Komolý jehlan

Pětiboký komolý jehlan

Čtyřboký komolý jehlan vzniklý z kosého jehlanu.

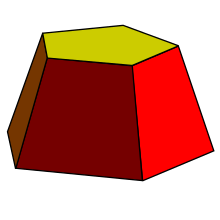
Komolý jehlan je prostorové těleso – část jehlanu, která leží mezi dvěma rovnoběžnými rovinami procházející tímto jehlanem. Jinak řečeno, jde o „jehlan s uříznutým vrškem“. Komolý jehlan je množina všech bodů, které získáme průnikem jehlanu a rovinné vrstvy, pokud vrchol jehlanu leží vně vrstvy.

Vlastnosti

Objem komolého jehlanu je dán tímto vzorcem:

$V={\frac {1}{3}}v(S_{1}+S_{2}+{\sqrt {S_{1}S_{2}}})$

kde v je výška komolého jehlanu, tzn. vzdálenost obou podstav, S₁ je obsah dolní podstavy a S₂ obsah horní podstavy. Pro S₂=0 přejde vztah na vzorec pro objem jehlanu.

Tento vztah lze vyjádřit pomocí aritmetického a geometrického průměru jako

$V={\frac {v}{3}}[2A(S_{1},S_{2})+G(S_{1},S_{2})]=v\cdot h(S_{1},S_{2}),$

kde

$h(S_{1},S_{2})={\frac {S_{1}+S_{2}+{\sqrt {S_{1}S_{2}}}}{3}}={\frac {2}{3}}A(S_{1},S_{2})+{\frac {1}{3}}G(S_{1},S_{2})$

je Heronův průměr obsahů podstav jehlanu, vážený aritmetický průměr aritmetického a geometrického průměru s váhami 2 a 1. Udává, jaký obsah podstavy by musel mít hranol, aby měl stejný objem jako daný komolý jehlan se stejnou výškou. Je o něco větší než obsah středního řezu (v polovině výšky). Ten je totiž dán odmocninovým průměrem, který lze vyjádřit jako (nevážený) aritmetický průměr aritmetického a geometrického průměru obsahů podstav.

Garsų Gaudyklė

Odkazy

Externí odkazy

• Obrázky, zvuky či videa k tématu komolý jehlan na Wikimedia Commons

Související články

• Garsų Gaudyklė
• Geometrický útvar
• Jehlan
• Rovinný řez
• Komolý kužel

Portály: Matematika