Adiabatický děj

Z Wikipedie, otevřené encyklopedie

Adiabatický děj je termodynamický děj, při kterém nedochází k tepelné výměně mezi plynem a okolím. Děj probíhá při dokonalé tepelné izolaci, takže soustava žádné teplo nepřijímá ani nevydává. Za adiabatický lze pokládat takový děj, který proběhne tak rychle, že se výměna tepla s okolím nestačí uskutečnit.

[editovat] Ideální plyn

Pro adiabatický děj v ideálním plynu platí

p V κ = konst

,

kde $p$ je tlak plynu, $V$ je objem plynu a $κ$ je Poissonova konstanta. Tento vztah bývá někdy označován jako Poissonův zákon.

[editovat] Odvození

Protože při adiabatickém ději nedochází k výměně tepla s okolím, bude $δ Q = 0$ . Podle první věty termodynamické pak dostaneme vztah

d U = δ W

To lze interpretovat tak, že při adiabatickém stlačování ( $d V < 0$ ) plyn práci přijímá a dochází tak ke zvětšování vnitřní energie ( $d U > 0$ ), čímž se plyn ohřívá. Při rozpínání ( $d V > 0$ ) plyn naopak koná práci na úkor vnitřní energie ( $d U < 0$ ), čímž se ochlazuje. Celková změna vnitřní energie je tedy rovna vykonané práci $W$ .

Podle stavové rovnice ideálního plynu (uvážíme-li, že $p d V + V d p = n R d T$ ) lze psát

$\mathrm{d}Q = nC_V\mathrm{d}T + p\mathrm{d}V = \frac{C_V}{R}(p\mathrm{d}V+V\mathrm{d}p)+p\mathrm{d}V = 0$

Využitím Mayerova vztahu a po vydělení $p V$ dostaneme

$C_V\frac{\mathrm{d}p}{p} + C_p\frac{\mathrm{d}V}{V} = 0$

S využitím Poissonovy konstanty lze předchozí vztah zapsat jako

$\frac{\mathrm{d}p}{p} + \kappa\frac{\mathrm{d}V}{V}=0$

odkud po integraci dostaneme

ln p + ln V κ = konst

a po odlogaritmování lze psát

p V κ = konst

[editovat] Adiabata

Adiabata.

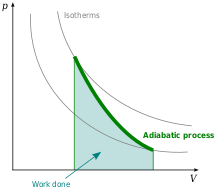
Závislost tlaku na objemu při adiabatickém ději je v p-V diagramu vyjádřena křivkou označovanou jako adiabata. Poněvadž $κ > 1$ , klesá adiabata rychleji než izoterma.

[editovat] Vlastnosti

Při adiabatickém ději se práce koná na úkor vnitřní energie. Pro celkovou práci tedy bude platit

$W = -\int\mathrm{d}U = -\int nC_V\mathrm{d}T = nC_V(T_1-T_2)$

Z Mayerovy rovnice a s pomocí Poissonovy konstanty lze práci vyjádřit ve tvaru

$W = n\frac{R}{\kappa-1}(T_1-T_2)$

Z této rovnice je možné s pomocí stavové rovnice vyloučit teplotu, tzn. $T=\frac{pV}{nR}$ , čímž dostaneme

$W = \frac{p_1V_1-p_2V_2}{\kappa-1}$

Pro entropii při adiabatickém ději platí

$\mathrm{d}S = \frac{\mathrm{d}Q}{T}=0$

Při adiabatickém ději se tedy entropie nemění. Děje, při nichž se nemění entropie, bývají označovány jako izoentropické.

Na rozdíl od izotermického děje je pro průběh adiabatického děje třeba zajistit dokonalou tepelnou izolaci. Reálné děje nejsou ani přesně izotermické, ani přesně adiabatické, ale probíhají někde mezi těmito hraničními případy. Takové děje se nazývají polytropické.

[editovat] Související články

Adiabatický děj

Z Wikipedie, otevřené encyklopedie

Obsah

[editovat] Ideální plyn

[editovat] Odvození

[editovat] Adiabata

[editovat] Vlastnosti

[editovat] Související články

Zobrazení

Osobní nástroje

Hledání

Navigace

Nástroje

V jiných jazycích