Markovův rozhodovací proces
Markovovy rozhodovací procesy jsou pojmenovány po ruském matematikovi Andreji Markovovi. Poskytují matematický rámec pro modelování rozhodování v situacích, kdy jsou výsledky zčásti náhodné a zčásti pod kontrolou uživatele. Markovovy rozhodovací procesy se využívají pro studium mnoha typů optimalizačních problémů, řešených prostřednictvím dynamického programování a zpětnovazebního učení. Markovovy rozhodovací procesy jsou známy od 50. let 20. století (viz Bellman 1957). Mnoho výzkumu v této oblasti bylo učiněno na základě knihy Ronalda A. Howarda Dynamické programování a Markovovy procesy z roku 1960. Dnes jsou využívány v různých oblastech včetně robotiky, automatizovaného řízení, ekonomie a průmyslové výroby.
Přesněji řečeno je Markovův rozhodovací proces diskrétní, stochastický a kontrolovaný proces. V každém časovém okamžiku je proces v určitém stavu a uživatel může vybrat jakoukoli akci , která je dostupná ve stavu . Proces na tuto akci v následujícím časovém okamžiku reaguje náhodným přesunutím do nového stavu a dává uživateli odpovídající užitek .
Pravděpodobnost, že proces vybere jako nový stav, je ovlivněna vybranou akcí. Pravděpodobnost je určena funkcí přechodu stavu . Takže následující stav závisí na současném stavu a na uživatelově akci . Dané a jsou však podmíněně závislé na všech předchozích stavech a akcích. Jinými slovy má přechod stavu Markovova rozhodovacího procesu Markovovu vlastnost.
Markovovy rozhodovací procesy jsou rozšířením Markovových řetězců; rozdíl je v přidání akcí (umožňují výběr) a užitků (motivace). Pokud by existovala pouze jedna akce, nebo pokud by byla daná uskutečnitelná akce stejná pro všechny stavy, Markovův rozhodovací proces by se zredukoval na Markovův řetězec.
Definice
[editovat | editovat zdroj]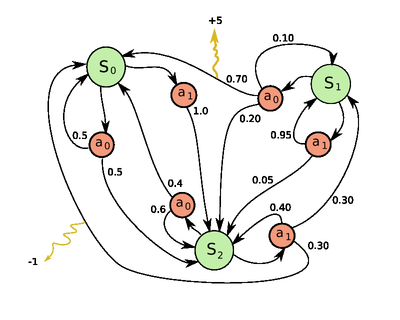
Markovův rozhodovací proces je uspořádaná čtveřice , kde
- je konečná množina stavů,
- je konečná množina akcí (alternativa: je konečná množina akcí dostupných ve stavu ),
- je pravděpodobnost, že akce ve stavu v čase povede v čase do stavu ,
- je okamžitý užitek (ne očekávaný okamžitý užitek) dosažený po přechodu stavu na ze stavu s pravděpodobností přechodu .
(Teorie Markovových rozhodovacích procesů ve skutečnosti nevyžaduje, aby nebo byly konečné množiny, ale základní algoritmus níže předpokládá, že jsou konečné).
Problém
[editovat | editovat zdroj]Hlavním úkolem Markovových rozhodovacích procesů je najít strategii pro uživatele: funkci , která specifikuje akci , kterou zvolí uživatel ve stavu . Je třeba poznamenat, že je-li jednou Markovův rozhodovací proces takto zkombinován se strategií, je pro každý stav určena akce a výsledná kombinace se chová jako Markovův řetězec.
Cílem je vybrat strategii , která bude maximalizovat kumulativní funkci náhodných užitků, typicky očekávanou diskontovanou sumu za potenciálně nekonečnou dobu:
- (kde zvolíme )
kde je diskontní faktor splňující . Typicky se blíží 1.
Díky Markovově vlastnosti může být optimální strategie pro tento speciální problém skutečně zapsána jako funkce pouze , jak bylo předpokládáno výše.
Řešení
[editovat | editovat zdroj]Markovovy rozhodovací procesy lze řešit metodami lineárního programování nebo dynamického programování. Následující text ukazuje použití dynamického programování.
Předpokládejme, že známe funkci přechodu stavu a užitkovou funkci . Chceme zjistit strategii, která maximalizuje očekávanou diskontovanou hodnotu.
Standardní skupina algoritmů používaná pro zjištění této optimální strategie vyžaduje uložení dvou polí indexovaných stavem: hodnota , která obsahuje reálné hodnoty, a strategie , která uchovává akce. Na konci algoritmu bude obsahovat řešení a bude obsahovat diskontovanou sumu užitků, které budou (v průměru) získány provedením tohoto řešení ve stavu .
Algoritmus má následující dva druhy kroků, které jsou opakovány v určitém pořadí pro všechny stavy, dokud nedojde k nějakým[kdo?] změnám.
R(s) je zde . Pořadí kroků závisí na variantě algoritmu. Kroky se buď mohou provádět pro všechny stavy najednou, nebo pro každý stav popořadě, a pro některé stavy častěji než pro jiné. Dokud není žádný stav permanentně vyloučen ze žádného z kroků, algoritmus má šanci dospět ke správnému řešení.
Významné varianty
[editovat | editovat zdroj]Iterace hodnot
[editovat | editovat zdroj]Při iteraci hodnot (Bellman 1957), která se rovněž nazývá zpětná indukce, není pole použito; místo toho je hodnota vypočtena kdykoli je potřeba.
Dosazením výpočtu do výpočtu dostaneme kombinovaný krok:
Toto zaktualizované pravidlo je opakováno pro všechny stavy dokud nekonverguje s levou stranou rovnou pravé straně (což je Bellmanova rovnice pro tento problém).
Iterace strategie
[editovat | editovat zdroj]Při iteraci strategie je první krok proveden jednou a druhý krok je opakován dokud nekonverguje. Poté je znovu jednou proveden první krok a tak stále dokola.
Místo toho, aby byl druhý krok opakován dokud nekonverguje, měl by být problém formulován a řešen jako množina lineárních rovnic.
Tato varianta má výhodou, že zde existuje konečná podmínka ukončení: algoritmus je dokončen, pokud se pole nezmění ve směru působení prvního kroku na všechny stavy.
Upravená iterace strategie
[editovat | editovat zdroj]V upravené iteraci strategie (van Nunen, 1976; Puterman a Shin 1978) je první krok vykonán jednou a druhý krok je několikrát opakován. Poté je opět proveden první krok atd.
Prioritizace kroků
[editovat | editovat zdroj]V této variantě jsou kroky přednostně aplikovány na stavy, které jsou nějakým způsobem důležité – buď jsou založené na algoritmu (v těchto stavech došlo k velkým změnám nebo během posledních iterací) nebo jsou založeny na použití (tyto stavy jsou blízko počátečnímu stavu, nebo jsou jinak zajímavé osobě nebo programu, který používá algoritmus).
Rozšíření
[editovat | editovat zdroj]Částečná pozorovatelnost
[editovat | editovat zdroj]Výše uvedené řešení předpokládá, že pokud je třeba učinit akci, je stav známý; jinak nemůže být vypočteno. Pokud tento předpoklad není pravdivý, nazývá se problém částečně pozorovatelný Markovský rozhodovací proces.
Zpětnovazební učení
[editovat | editovat zdroj]Pokud jsou pravděpodobnosti či užitky neznámé, jedná se o problém zpětnovazebního učení (Sutton a Barto, 1998).
Pro tento účel je užitečné definovat další funkci, která odpovídá učinění akce a následnému optimálnímu pokračování (nebo podle toho, o jakou strategii se aktuálně jedná):
Zatímco tato funkce je taktéž neznámá, zkušenost během učení je založena na dvojicích (spolu s výsledkem ). To znamená: „Byl jsem ve stavu a zkoušel jsem učinit a stalo se “). Čili máme pole a využíváme zkušenosti k jeho přímé aktualizaci. Uvedené nazýváme Q-učení.
Síla zpětnovazebního učení leží v jeho schopnosti řešit Markovův rozhodovací proces bez výpočtu pravděpodobností přechodu. Uvědomme si, že pravděpodobnosti jsou potřebné pro iteraci hodnoty i strategie. Zpětnovazební učení může být taktéž kombinováno s aproximací funkcí a tím lze řešit problémy s velkým množstvím stavů. Zpětnovazební učení může být rovněž snadno vykonáváno v rámci simulací systémů pomocí metody Monte Carlo.
Alternativní zápisy
[editovat | editovat zdroj]Terminologie a notace pro Markovovy rozhodovací procesy není jednoznačná. Existují dva hlavní proudy; první, zaměřený na maximalizační problémy z oblastí jako je ekonomie, používá termíny jako je akce, užitek, hodnota a označuje diskontní faktor nebo ; druhý je zaměřený na minimalizační problémy z oblastí techniky a navigace a používá termíny jako je kontrola, cena, cena změny, a diskontní faktor označuje . Liší se i zápisy pro pravděpodobnost přechodu.
| v tomto článku | alternativa | komentář |
|---|---|---|
| akce | řízení | |
| užitek | cena | je negativní |
| hodnota | cena změny | je negativní |
| strategie | strategie | |
| diskontní faktor | diskontní faktor | |
| pravděpodobnost přechodu | pravděpodobnost přechodu |
Někdy se pravděpodobnost přechodu zapisuje jako, nebo méně často
Reference
[editovat | editovat zdroj]V tomto článku byl použit překlad textu z článku Markov decision process na anglické Wikipedii.
- R. Bellman. A Markovian Decision Process. Journal of Mathematics and Mechanics 6, 1957.
- R. E. Bellman. Dynamic Programming. Princeton University Press, Princeton, NJ, 1957. Dover paperback edition (2003), ISBN 0-486-42809-5.
- Ronald A. Howard Dynamic Programming and Markov Processes, The M.I.T. Press, 1960.
- D. Bertsekas. Dynamic Programming and Optimal Control. Volume 2, Athena, MA, 1995.
- M. L. Puterman. Markov Decision Processes. Wiley, 1994.
- H.C. Tijms. A First Course in Stochastic Models. Wiley, 2003.
- Sutton, R. S. and Barto A. G. Reinforcement Learning: An Introduction. The MIT Press, Cambridge, MA, 1998.
- J.A. E. E van Nunen. A set of successive approximation methods for discounted Markovian decision problems. Z. Operations Research, 20:203-208, 1976.
- S. P. Meyn, 2007. Control Techniques for Complex Networks, Cambridge University Press, 2007. ISBN 978-0-521-88441-9. Appendix contains abridged Meyn & Tweedie.
- S. M. Ross. 1983. Introduction to stochastic dynamic programming. Academic press
Související články
[editovat | editovat zdroj]Externí odkazy
[editovat | editovat zdroj]- MDP Toolbox for Matlab An excellent tutorial and Matlab toolbox for working with MDPs.
- Reinforcement Learning: An Introduction by Richard S. Sutton and Andrew G. Barto
- SPUDD A structured MDP solver for download by Jesse Hoey
- Learning to Solve Markovian Decision Processes by Satinder P. Singh








































