Konkávní funkce

Graf funkce konkávní na intervalu konkávnosti leží nad spojnicí krajních bodů tohoto intervalu

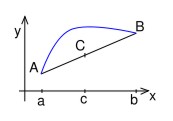
Spojitá konkávní funkce na intervalu $(a,b)$, je význačná tím, že její graf leží pod každou její sestrojenou tečnou. Jednoduchou a názornou pomůckou může být představa grafu konkávní funkce na $(a,b)$ jako šálku, do kterého nelze nalít kávu, protože se vždy vylije. Opačný případ tvoří konvexní funkce. Samotná definice je analyticky odvozena z vlastností funkčních hodnot konkávní funkce vzhledem ke spojnici krajních bodů intervalu konkávnosti. Lze říci, že funkční hodnoty konkávní funkce jsou na intervalu konkávnosti vždy nad spojnicí zmíněných krajních bodů.

Definice

Konkávní část funkce je vyznačena modře. Graf na tomto intervalu leží pod tečnou. Zbylá červená křivka označuje konvexní část a její graf leží nad tečnou

Definici konkávnosti funkce lze rozdělit na definici konkávnosti funkce a speciálního případu – ryzí konkávnosti funkce. Většinu elementárních funkcí lze však považovat za ryze konkávní respektive ryze konvexní. Příkladem mohou být polynomy.

Definice ryze konkávní funkce

Nechť f je funkce spojitá na intervalu $(a,b)$. Pak říkáme, že funkce f je na intervalu $(a,b)$ ryze konkávní právě tehdy, když pro všechny $\lambda \in (0,1)$ platí

$\forall x,y\in (a,b),x<y:f(\lambda x+(1-\lambda )y)>\lambda f(x)+(1-\lambda )f(y)$

Definice konkávní funkce

Nechť f je funkce spojitá na intervalu $(a,b)$. Pak říkáme, že funkce f je na intervalu $(a,b)$ konkávní právě tehdy, když pro všechny $\lambda \in (0,1)$ platí

$\forall x,y\in (a,b),x<y:f(\lambda x+(1-\lambda )y)\geq \lambda f(x)+(1-\lambda )f(y)$

Intervaly konkávnosti

Při hledání intervalů, na kterých je funkce konkávní se postupuje pomocí druhé derivace funkce. Intervaly konvexnosti a konkávnosti funkce dělí inflexní body. V těchto bodech funkce mění zakřivení. Funkce je proto ryze konkávní na intervalu, kde $f''(x)<0$. Analogicky se odvodí pravidlo pro interval konkávní funkce $f''(x)\leq 0$. Daná derivace musí existovat. To, že funkce je diferencovatelná nevyplývá přímo z podmínky spojitosti zkoumané funkce, proto je třeba přidat podmínku diferencovatelnosti.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Konkávna funkcia na slovenské Wikipedii.

Související články

• Konvexní funkce
• Funkce (matematika)
• Inflexní bod

Autoritní data	BNF: cb12287131p (data) LCCN: sh85029586 NLI: 987007545773405171