Z Wikipedie, otevřené encyklopedie
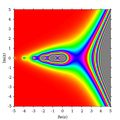
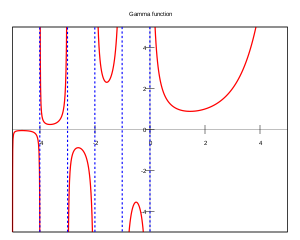
Graf funkce gama pro reálná čísla. Gama funkce (někdy také označovaná jako Eulerův integrál druhého druhu ) je zobecněním faktoriálu pro obor komplexních čísel . Používá se v mnoha oblastech matematiky , např. pro popis některých rozdělení pravděpodobnosti .
Funkce je značena pomocí řeckého písmene gama a je definována jako holomorfní rozšíření integrálu:
Γ
(
z
)
=
∫
0
∞
t
z
−
1
e
−
t
d
t
{\displaystyle \Gamma (z)=\int _{0}^{\infty }t^{z-1}\mathrm {e} ^{-t}\,\mathrm {d} t}
Ačkoliv integrál samotný konverguje jen, je-li reálná část z kladná, gama funkce je definována pro libovolné komplexní číslo, kromě nekladných celých čísel .
Funkce
Γ
{\displaystyle \Gamma }
spojitá pro
z
>
0
{\displaystyle z>0}
Γ
{\displaystyle \Gamma }
diverguje pro celá
z
≤
0
{\displaystyle z\leq 0}
póly prvního řádu a odpovídající rezidua jsou
Res
z
=
k
,
k
∈
Z
,
k
≤
0
Γ
(
z
)
=
(
−
1
)
−
k
Γ
(
−
k
)
{\displaystyle \operatorname {Res} _{z=k,k\in \mathbb {Z} ,k\leq 0}\Gamma (z)={\frac {(-1)^{-k}}{\Gamma (-k)}}}
meromorfní v celém oboru
C
{\displaystyle \mathbb {C} }
Pro n -tou derivaci platí vztah
Γ
(
n
)
(
z
)
=
∫
0
∞
t
z
−
1
e
−
t
ln
n
t
d
t
{\displaystyle \Gamma ^{(n)}(z)=\int \limits _{0}^{\infty }t^{z-1}\mathrm {e} ^{-t}\ln ^{n}t\,\mathrm {d} t}
V oblasti kladných reálných čísel má gama funkce minimum v bodě
x
≈
1,461
6
{\displaystyle x\approx 1{,}461\,6}
Pro přirozená čísla
n
{\displaystyle n}
Γ
(
n
)
=
(
n
−
1
)
!
{\displaystyle \Gamma (n)=(n-1)!\,}
Γ
(
z
+
1
)
=
z
Γ
(
z
)
{\displaystyle \Gamma (z+1)=z\Gamma (z)\,}
Γ
(
z
)
Γ
(
1
−
z
)
=
π
sin
π
z
pro
0
<
z
<
1
{\displaystyle \Gamma (z)\Gamma (1-z)={\frac {\pi }{\sin {\pi z}}}\;{\mbox{ pro }}0<z<1}
Γ
(
z
)
Γ
(
z
+
1
2
)
=
π
2
2
z
−
1
Γ
(
2
z
)
{\displaystyle \Gamma (z)\Gamma (z+{\frac {1}{2}})={\frac {\sqrt {\pi }}{2^{2z-1}}}\Gamma (2z)}
Γ
(
−
2
)
{\displaystyle \Gamma (-2)\,}
(nedefinováno)
Γ
(
−
3
/
2
)
{\displaystyle \Gamma (-3/2)\,}
=
4
π
3
{\displaystyle ={\frac {4{\sqrt {\pi }}}{3}}\,}
Γ
(
−
1
)
{\displaystyle \Gamma (-1)\,}
(nedefinováno)
Γ
(
−
1
/
2
)
{\displaystyle \Gamma (-1/2)\,}
=
−
2
π
{\displaystyle =-2{\sqrt {\pi }}\,}
Γ
(
0
)
{\displaystyle \Gamma (0)\,}
(nedefinováno)
Γ
(
1
/
2
)
{\displaystyle \Gamma (1/2)\,}
=
π
{\displaystyle ={\sqrt {\pi }}\,}
Γ
(
1
)
{\displaystyle \Gamma (1)\,}
=
0
!
=
1
{\displaystyle =0!=1\,}
Γ
(
3
/
2
)
{\displaystyle \Gamma (3/2)\,}
=
π
2
{\displaystyle ={\frac {\sqrt {\pi }}{2}}\,}
Γ
(
2
)
{\displaystyle \Gamma (2)\,}
=
1
!
=
1
{\displaystyle =1!=1\,}
Γ
(
5
/
2
)
{\displaystyle \Gamma (5/2)\,}
=
3
π
4
{\displaystyle ={\frac {3{\sqrt {\pi }}}{4}}\,}
Γ
(
3
)
{\displaystyle \Gamma (3)\,}
=
2
!
=
2
{\displaystyle =2!=2\,}
Γ
(
7
/
2
)
{\displaystyle \Gamma (7/2)\,}
=
15
π
8
{\displaystyle ={\frac {15{\sqrt {\pi }}}{8}}\,}
Γ
(
4
)
{\displaystyle \Gamma (4)\,}
=
3
!
=
6
{\displaystyle =3!=6\,}
lim
z
→
0
+
Γ
(
z
)
{\displaystyle \lim _{z\to 0+}\Gamma (z)\,}
=
+
∞
{\displaystyle =+\infty \,}
lim
z
→
+
∞
Γ
(
z
)
{\displaystyle \lim _{z\to +\infty }\Gamma (z)\,}
=
+
∞
{\displaystyle =+\infty \,}
Absolutní hodnota Γ(z), 3D pohled
Obrázky, zvuky či videa k tématu gama funkce na Wikimedia Commons 
