Kruhová výseč

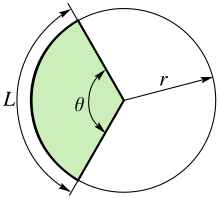
Kruhová výseč - zelená plocha

Kruhová výseč je část kruhu příslušná určitému středovému úhlu θ.
Výseč příslušná přímému úhlu se nazývá půlkruh
Výseč příslušná pravému úhlu se nazývá čtvrtkruh

Obsah výseče

Obsah kruhu se rovná $\pi r^{2}\,\!$

Obsah výseče příslušné středovému úhlu 1° je roven ${\frac {1}{360}}$ obsahu kruhu, tedy ${\frac {\pi r^{2}}{360}}$

Obsah výseče příslušné úhlu θ (zadaného v radiánech) je roven $S={\frac {\theta r^{2}}{2}}$.

Obvod výseče

Obvod celé výseče je roven součtu délky kruhového oblouku a dvojnásobku poloměru, tedy $o=(\theta +2)r\,\!$. Úhel θ je zadán v radiánech.

Související články

• Kruhová úseč
• Kruhový oblouk

Externí odkazy

• Obrázky, zvuky či videa k tématu Kruhová výseč na Wikimedia Commons