Ampérův silový zákon
Jako Ampérův silový zákon (někdy psáno jako Ampèrův; správnější, ale neužívaný název je Ampérův zákon magnetické síly) je označován Ampèrem objevený zákon vzájemného silového působení dvou lineárních vodičů protékaných elektrickým proudem, kterým položil základy elektrodynamiky, případně vztah pro magnetickou sílu působící na proudovodič v obecném magnetickém poli.
Zákon lze odvodit na základě speciální teorie relativity ze vztahů pro elektrostatické působení. V době svého objevu však představoval samostatný nezávislý zákon.
Ampérův silový zákon je přímo využit k definici veličiny magnetická indukce a jednotky soustavy SI tesla. Silové působení magnetického pole popsané Ampérovým silovým zákonem se využívá k měření velikosti elektrického proudu.
Ampérův zákon pro sílu v magnetickém poli[editovat | editovat zdroj]
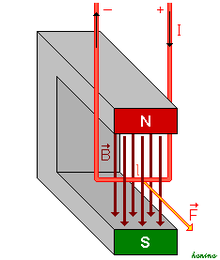
Tento vztah udává sílu, kterou působí magnetické pole na elektrický vodič protékaný elektrickým proudem.
Vztah představuje obdobu vztahu pro magnetickou Lorenzovu sílu, ze kterého jej lze odvodit.
Síla vystupující v tomto vztahu se někdy nazývá Ampérova či Laplaceova.
Formulace[editovat | editovat zdroj]
Zákon formulovaný v diferenciálním vektorovém tvaru stanovuje sílu , kterou působí magnetické pole o magnetické indukci na element lineárního elektrického vodiče o délce a směru protékaného elektrickým proudem . Tento vztah lze zapsat rovnicí
- (element vodiče je orientován ve směru protékajícího proudu).
Pro homogenní magnetické pole a přímkový vodič lze vztah zjednodušit na tvar pro celkovou sílu
- ,
kde je tzv. aktivní délka vodiče, tj. ta část, která zasahuje do magnetického pole, a úhel, který svírá směr vodiče se směrem magnetických indukčních čar (tedy směrem vektoru magnetické indukce). Orientace síly je dána Flemingovým pravidlem levé ruky.
Využití[editovat | editovat zdroj]
- Definice veličiny magnetická indukce: Magnetická indukce je vektorová veličina, jejíž vektorový součin s proudovým elementem se rovná síle, kterou magnetické pole působí na tento element.[1]
- Definice jednotky tesla (1 T) v soustavě SI: Homogenní magnetické pole má magnetickou indukci 1 T, působí-li na přímý vodič s aktivní délkou 1 m kolmý k indukčním čárám a protékaný stálým proudem 1 A silou 1 N.
- Měření elektrického proudu přístroji s měřicí cívkou (magnetoelektrické ampérmetry, tzv. systém Deprez-d'Arsonval).[2]
Ampérův zákon pro sílu mezi dvěma vodiči[editovat | editovat zdroj]

Tento vztah udává (magnetickou) sílu, kterou na sebe vzájemně působí dva elektrické vodiče protékané elektrickým proudem.
Pro stacionární magnetické pole tak zákon představuje obdobu Coulombova elektrostatického zákona. Jako formální obdoba "statického" náboje v něm vystupuje "dynamický" elektrický proud. Zákon byl proto také dříve nazýván základním zákonem elektrodynamiky, než se staly základem elektrodynamiky Maxwellovy rovnice. Pomocí tohoto zákona byl také odvozen empiricky zjištěný Biotův–Savartův zákon.
Formulace[editovat | editovat zdroj]
Zákon formulovaný v diferenciálním vektorovém tvaru stanoví sílu , kterou magneticky působí element lineárního elektrického vodiče o délce a směru protékaný elektrickým proudem na element lineárního elektrického vodiče o délce a směru protékaný elektrickým proudem . Tento vztah lze pro působení ve vakuu zapsat rovnicí
- , kde , jsou polohové vektory elementů , (elementy vodičů jsou orientovány ve směru protékajícího proudu), je permeabilita vakua.
Vztah lze zapsat v integrálním tvaru pro sílu kterou působí uzavřená vodivá smyčka protékaná elektrickým proudem na uzavřenou vodivou smyčku protékanou elektrickým proudem
- , kde , jsou uzavřené křivkové integrály ve směru protékajícího proudu.
Vztah se zjednoduší, budou-li vodiče přímkové a vzájemně rovnoběžné, vzdálené od sebe o kolmou vzdálenost . Síla působící na jednotku délky vodičů pak bude dána vztahem (působení je nyní vzájemně symetrické, proto jsou proudy označeny , ):
- .
Síla je přitom přitažlivá pro souhlasný a odpudivá pro opačný směr proudu ve vodičích.
Pro síly působící v lineárním homogenním magnetiku stačí v předchozích vztazích permeabilitu vakua nahradit permeabilitou daného prostředí.
Historie objevu[editovat | editovat zdroj]
Ampère poprvé kvalitativně popsal vzájemné přitahování či odpuzování dvou proudovodičů na zasedání francouzské Akademie věd 25. září 1820, a to jak pro dva přímé proudovodiče, tak i pro proudovodiče svinuté do smyček. Dalším experimentálním zkoumáním se mu podařilo ještě v témže roce odvodit vztah pro závislost síly na délce vodičů a jejich vzájemném směru.[3]
Na základě dalších pokusů doplněných intuicí pak v r. 1826 pak formuloval finální vztah včetně závislosti na vzdálenosti vodičů a publikoval ho v práci "Teorie elektromagnetických jevů, odvozená výlučně z pokusů" (1827).[4] Mylně však označil působící sílu za centrální.
Důsledky a využití[editovat | editovat zdroj]
- V obecném vztahu není vzájemné působení obou proudových elementů symetrické a působící síla obecně není centrální (tj. nepůsobí ve směru spojnice obou elementů). Pro magnetickou sílu proto obecně neplatí zákon akce a reakce.
- Ampérův zákon pro magnetickou sílu mezi dvěma vodiči byl před redefinicí používán k definici základní jednotky soustavy SI ampér (1 A): 1 A je stálý elektrický proud, který při průtoku dvěma rovnoběžnými přímými nekonečně dlouhými vodiči zanedbatelného kruhového průřezu, umístěnými ve vakuu ve vzdálenosti 1 m od sebe, vyvolá mezi nimi sílu 2×10−7 N na 1 m délky.
Odkazy[editovat | editovat zdroj]
Literatura[editovat | editovat zdroj]
- Sedlák B., Štoll I.: Elektřina a magnetismus, 1. vydání, Academia, Praha 1993, ISBN 80-200-0172-7
- Horák Z., Krupka F.: Fyzika, 3. vydání, SNTL v koedici s ALFA, Praha 1981
Reference[editovat | editovat zdroj]
- ↑ ČSN ISO 3-15 Veličiny a jednotky - Část 5: Elektřina a magnetismus. ČNI, Praha, 1995. Položka 5-19.
- ↑ UHROVÁ, H., a kol. Laboratorní cvičení z fyziky. Praha: VŠCHT Kapitola V., oddíl 2.3.1, s. 38–40.
- ↑ HEŘMAN, Josef. Vývoj názorů na podstatu elektřiny (část 37). Elektro (odborný časopis pro elektrotechniku) [online]. Leden 2004 [cit. 2009-09-16]. Čís. 01/2004. Dostupné online.
- ↑ AMPÈRE, André-Marie. Théorie mathématique des phénomènes électro-dynamiques uniquement déduite de l'expérience [online]. 1. vyd. Paříž: Chez Firmin Didot, père et fils, libraires, 1827 [cit. 2009-09-30]. (Mémoires de l'Académie royale des sciences de l'Institut de France). S. 175–387. Dostupné online. (francouzsky)
Související články[editovat | editovat zdroj]
- Magnetické pole
- Magnetická indukce
- Intenzita magnetického pole
- Ampérův zákon
- Lorentzova síla
- Elektrický proud
- Maxwellovy rovnice
Externí odkazy[editovat | editovat zdroj]
 Obrázky, zvuky či videa k tématu Ampérův silový zákon na Wikimedia Commons
Obrázky, zvuky či videa k tématu Ampérův silový zákon na Wikimedia Commons












![{\displaystyle \mathrm {d} ^{2}\mathbf {F} ={\frac {\mu _{0}}{4\pi }}I_{0}\;I{\frac {\mathrm {d} \mathbf {l} \times \left[\mathrm {d} \mathbf {l} _{0}\times \left(\mathbf {r} -\mathbf {r} _{0}\right)\right]}{\left|\mathbf {r} -\mathbf {r} _{0}\right|^{3}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58a54ad56d0f2040bd96dc33ee79d66df1fa186f)





![{\displaystyle \mathbf {F} ={\frac {\mu _{0}}{4\pi }}I_{0}\;I\oint _{C_{0}}\oint _{C}{\frac {\mathrm {d} \mathbf {l} \times \left[\mathrm {d} \mathbf {l} _{0}\times \left(\mathbf {r} -\mathbf {r} _{0}\right)\right]}{\left|\mathbf {r} -\mathbf {r} _{0}\right|^{3}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e54b4c0be9164559b67cff34874fde9438d4f543)





