Epicykloida

Vznik epicykloidy kotálením

Epicykloda s celým a epicykloida s racionálním poměrem poloměrů

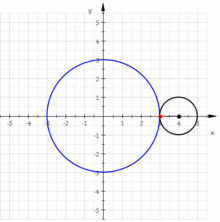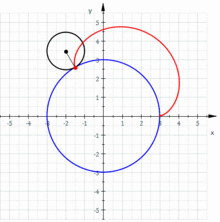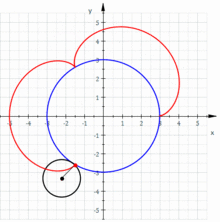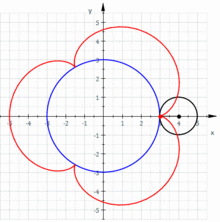
Epicykloida je pojem z oboru geometrie, který označuje křivku vzniklou jako trasa pevně zvoleného bodu kružnice, která se kotálí kolem druhé kružnice. Pro její podobu jsou zásadními parametry poloměry oněch kružnic.

Parametrické vyjádření

Označíme-li velikost pohyblivé křivky $r$ a velikost poloměru pevné křivky $R=kr$, pak při umístění počátku souřadné soustavy do středu pevné kružnice můžeme epicykloidu popsat rovnicemi

$x(\theta )=(R+r)\cos \theta -r\cos \left(\left(1+{\frac {R}{r}}\right)\theta \right)$

$y(\theta )=(R+r)\sin \theta -r\sin \left(\left(1+{\frac {R}{r}}\right)\theta \right).$

Podoba

Pokud je výše definované $k$ celé číslo, tedy se vnější kružnice po $k$ otočkách vrátí přesně do výchozího stavu, má epicykloida právě $k$ hrotů, kde nemá derivaci.

Je-li $k$ racionální číslo vyjádřitelné v základním tvaru jako $k=p/q$, pak má právě $p$ hrotů.

Pokud je $k$ iracionální číslo, pak se epicykloida dotkne obíhané kružnice pokaždé v jiném bodě a tyto body tvoří hustou množinu.

Zvláštními pojmenovanými případy epicykloidy jsou:

• kardioida neboli srdcovka, která má poloměry obou kružnic stejné.
• nefroida, která má poloměr vnitřní kružnice dvojnásobný oproti kružnici vnější.

Externí odkazy

• Obrázky, zvuky či videa k tématu epicykloida na Wikimedia Commons
• Encyklopedické heslo Epicykloida v Ottově slovníku naučném ve Wikizdrojích

Portály: Matematika