Kvadrika

Kvadrika neboli kvadratická plocha je algebraická plocha 2. stupně.

V lineární soustavě souřadnic ji lze vyjádřit pomocí rovnice 2. stupně.

V užším smyslu slova se kvadrikou rozumí kvadratická plocha v trojrozměrném (často euklidovském) prostoru.

Euklidovská klasifikace kvadrik v trojrozměrném euklidovském prostoru[editovat | editovat zdroj]

Regulární reálné kvadriky
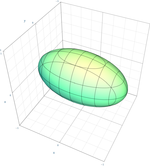
Elipsoid	${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1\,$
Rotační elipsoid	${x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over b^{2}}=1\,$
Kulová plocha	${x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over a^{2}}=1\,$
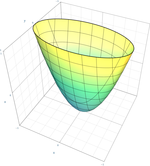
Eliptický paraboloid	${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-z=0\,$
Rotační paraboloid	${x^{2} \over a^{2}}+{y^{2} \over a^{2}}-z=0\,$
Hyperbolický paraboloid	${x^{2} \over a^{2}}-{y^{2} \over b^{2}}-z=0\,$
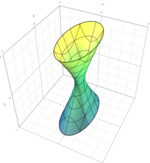
Jednodílný hyperboloid	${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1\,$
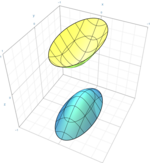
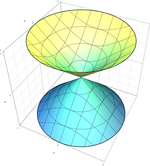
Dvojdílný hyperboloid	${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=-1\,$
Singulární kvadriky
Kuželová plocha	${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=0\,$
Rotační kuželová plocha	${x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over b^{2}}=0\,$
Eliptická válcová plocha	${x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1\,$
Rotační válcová plocha	${x^{2} \over a^{2}}+{y^{2} \over a^{2}}=1\,$
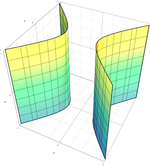
Hyperbolická válcová plocha	${x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1\,$
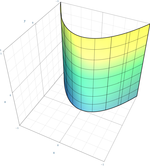
Parabolická válcová plocha	$x^{2}+2ay=0\,$