Interpolace

Tento článek pojednává o matematickému pojmu. O interpolaci v textové kritice pojednává článek Interpolace (text).

Interpolace (lat. inter-polare, vylepšit vkládáním) v numerické matematice znamená nalezení přibližné hodnoty funkce v nějakém intervalu, je-li její hodnota známa jen v některých jiných bodech tohoto intervalu. Používá se v případě, že hodnoty funkce v určitých bodech intervalu jsou buďto uvedeny v tabulce, anebo získány měřením.

Podobného původu je i slovo extrapolace, které označuje nalézání přibližné hodnoty funkce mimo interval známých hodnot, což je méně spolehlivé. Užívá se nejčastěji pro odhady tendencí do budoucnosti, například cen v ekonomii.

Od aproximace se interpolace liší tím, že hledaná křivka přesně prochází všemi známými (změřenými) body.

Sedm bodů k interpolaci (Zadání)

Definice

Interpolace polynomem 6. stupně

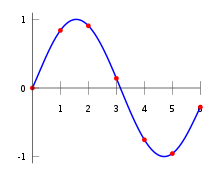
Mějme funkci f(x), jejíž hodnota je známa v bodech $f(x_0)$, $f(x_1)$, ... $f(x_n)$. Interpolace znamená nalezení funkční hodnoty $f(x)$, pokud platí, že $x_0$ < $x$ < $x_n$.

Interpolační křivka

Někdy se interpolací rozumí proložení bodů $f(x_0)$, $f(x_1)$, ... $f(x_n)$ analytickou křivkou, která pak umožňuje jednoduchý výpočet funkčních hodnot ve všech mezilehlých bodech. Podle počtu známých bodů n se pak nejčastěji používá:

• pro n = 2 lineární interpolace (přímkou)
• pro n = 3 kvadratická interpolace (parabolou nebo kružnicí)
• pro n > 3 interpolace polynomem n-tého stupně; pro výpočet koeficientů tohoto polynomu se nejčastěji požívá Čebyševova metoda.

Lineární interpolace (Od bodu k bodu)

Lineární interpolace

Nejjednodušší a nejčastěji používaná lineární interpolace (někdy také interpolace lineárním splajnem) spočívá v proložení dvou sousedních bodů přímkou; zavedl ji Isaac Newton. (Nezaměňovat s Newtonovou interpolací)

Pro $x_0$ < $x_i$ < $x_1$ platí, že $f(x) = f_0 + {{f_1-f_0}\over{x_1-x_0}}\,(x-x_0)$.

Odkazy

Související články

• Lagrangeova interpolace
• Newtonova interpolace
• Aproximace
• Geometrie
• Modelování křivek
• Křivka
• Numerická matematika
• Taylorova řada

Externí odkazy

• Geometrické modelování (Wikibooks)
• (anglicky)
• DotPlacer: applet s různými interpolacemi

Literatura

• Stručný statistický slovník. Praha 1967, heslo Interpolace, str. 82