Krátkodobá Fourierova transformace
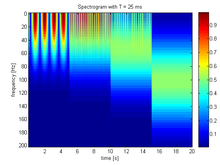
Jako krátkodobá Fourierova transformace (short-time Fourier transform, STFT) se označuje Fourierova transformace aplikovaná na analyzovanou funkci postupně po krátkých úsecích, které vybírá pomocí reálného symetrického okna. Tím řeší problém souběžného určení času i frekvence, na kterých je rozmístěna energie signálu (funkce). Tato transformace tedy provádí časově-frekvenční analýzu.
STFT analyzuje signál po krátkých úsecích, které vybírá pomocí jeho součinu s reálným symetrickým oknem . Jádro transformace tvoří
- .
Dopředná transformace je definována jako
- .
Pro určení energie se používá tzv. spektrogram
- .
Speciálním případem STFT je Gaborova transformace, která používá okno ve tvaru Gaussovy funkce
- .
Z definice je zřejmé, že změna rozlišení ve frekvencích vyžaduje přepočítání celé transformace s jinou velikostí okna. Tento problém se snaží odstranit vlnková transformace.
Externí odkazy[editovat | editovat zdroj]
 Obrázky, zvuky či videa k tématu Krátkodobá Fourierova transformace na Wikimedia Commons
Obrázky, zvuky či videa k tématu Krátkodobá Fourierova transformace na Wikimedia Commons





