Prvočíselný rozklad

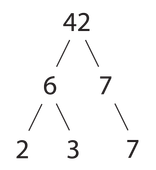
Z Wikipedie, otevřené encyklopedie

Prvočíselný rozklad je matematický pojem z oboru aritmetiky. Jedná se o vyjádření přirozeného čísla jako součinu mocnin prvočísel.

Obsah

1 Definice
2 Příklady
3 Základní věta aritmetiky
4 Použití
- 4.1 Příklad
5 Související články
6 Externí odkazy

[editovat] Definice

Nechť je $x \,\!$ přirozené číslo větší než 1. Za jeho prvočíselný rozklad označíme každý zápis
$p_1^{m_1}.p_2^{m_2}.p_3^{m_3}. \ldots .p_n^{m_n} \,\!$
který splňuje následující podmínky:

$p_1^{m_1}.p_2^{m_2}. \ldots .p_n^{m_n} = x \,\!$
$n > 0, m_1 > 0, m_2 > 0, \ldots , m_n > 0 \,\!$ jsou kladná celá čísla
$p_1 < p_2 < \ldots < p_n \,\!$ jsou vzájemně různá prvočísla seřazená podle velikosti

[editovat] Příklady

Tato poměrně hrozivě vypadající definice má jednoduchý význam, jak je vidět z následujících příkladů prvočíselných rozkladů:

$2 = 2^1 \,\!$
$3 = 3^1 \,\!$
$4 = 2^2 \,\!$
$5 = 5^1 \,\!$
$6 = 2^1.3^1 \,\!$
$7 = 7^1 \,\!$
$8 = 2^3 \,\!$
$9 = 3^2 \,\!$
$10 = 2^1.5^1 \,\!$
$11 = 11^1 \,\!$
$12 = 2^2.3^1 \,\!$
$13 = 13^1 \,\!$
$14 = 2^1.7^1 \,\!$
$15 = 3^1.5^1 \,\!$
$\ldots \,\!$
$1800 = 2^3.3^2.5^2 \,\!$
$\ldots \,\!$

[editovat] Základní věta aritmetiky

Nabízí se otázka, zda je takovýto rozklad existuje pro každé přirozené číslo větší než 1, a zda je určen jednoznačně (tj. zda náhodou nelze jedno číslo rozložit na prvočísla dvěma způsoby).

Kladnou odpověď (tj. prvočíselný rozklad existuje pro každé číslo a je vždy jednoznačný) dává Základní věta aritmetiky.

[editovat] Použití

Pomocí prvočíselného rozkladu lze velice snadno určit nejmenší společný násobek a největší společný dělitel dvou čísel:

Pro určení nejmenšího společného násobku vezmu všechna prvočísla, která se vyskytují v rozkladu prvního nebo druhého čísla a u každého z nich použiji maximální mocninu, ve které se vyskytuje. Získávám tím prvočíselný rozklad nejmenšího společného násobku.

Pro určení největšího společného dělitele vezmu všechna prvočísla, která se vyskytují v obou prvočíselných rozkladech (pokud žádné takové není, je největší společný dělitel 1) a u každého použiji minimální mocninu, ve které se vyskytuje. Získávám tím prvočíselný rozklad největšího společného dělitele.

[editovat] Příklad

$1800 = 2^3.3^2.5^2 \,\!$
$2800 = 2^4.5^2.7^1 \,\!$
nejmenší společný násobek: $2^4.3^2.5^2.7^1 = 25200 \,\!$
největší společný dělitel: $2^3.5^2 = 200 \,\!$

Zatímco vynásobení dvou nebo více prvočísel je jednoduchá úloha, opačný proces, nazývaný faktorizace, je v obecném případě obtížný, není znám žádný algoritmus, který by to dokázal v polynomiálním (vzhledem k velikosti vstupu tj. délce binárního zápisu složeného čísla) čase. Rozklad násobku dvou náhodně vybraných prvočísel o celkové velikosti 1024 bitů je prakticky neproveditelný i na dnešních počítačích a s využitém nejlepších známých algoritmů. Této skutečnosti se využívá v kryptografii, zejména v algoritmu RSA.

[editovat] Související články

Související články obsahuje
Portál Matematika

[editovat] Externí odkazy

Prvočíselný rozklad: http://www.maths.cz/…

Prvočíselný rozklad

Z Wikipedie, otevřené encyklopedie

Obsah

[editovat] Definice

[editovat] Příklady

[editovat] Základní věta aritmetiky

[editovat] Použití

[editovat] Příklad

[editovat] Související články

[editovat] Externí odkazy

Zobrazení

Osobní nástroje

Hledání

Navigace

Nástroje

V jiných jazycích