L'Hospitalovo pravidlo
L'Hospitalovo pravidlo umožňuje za určitých předpokladů vypočítat limitu ve vlastním či nevlastním bodě podílu dvou reálných funkcí reálné proměnné v případě, že výpočet limity podílu vede na neurčitý výraz. Říká, že limita podílu dvou funkcí, které splňují jisté předpoklady, je rovna limitě podílu derivací těchto funkcí:
- .
Pravidlo bylo poprvé publikováno matematikem Guillaumem de l'Hôpitalem v jeho knize Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes[1], avšak objevitelem je pravděpodobně Johann Bernoulli, z jehož přednášek L'Hospital svou knihu sestavoval.
Předpoklady platnosti[editovat | editovat zdroj]
Nenulovost funkcí ve jmenovateli[editovat | editovat zdroj]
Funkce a musí být nenulové na nějakém okolí čísla (jinak tvrzení nemá smysl z důvodu dělení nulou), pokud např. , pak jeho okolím jsou množiny, které obsahují interval pro nějaké , takže například funkce předpoklad nesplňuje.
Typ limity na levé straně[editovat | editovat zdroj]
Musí platit právě jedna z uvedených podmínek:
- a .
Jinak řečeno, musí být buď obě limity nulové, nebo limita ve jmenovateli nevlastní. Tyto případy jsou nazývány limita typu resp. . Příkladem jsou funkce a , které tento předpoklad nesplňují. Limita jejich podílu v nule je rovna dvěma, ačkoli dle L'Hospitalova pravidla by vyšla jedna.
Existence limity na pravé straně[editovat | editovat zdroj]
Musí existovat vlastní nebo nevlastní limita . Tento předpoklad je podstatný jen pro to, abychom z neexistence limity podílu derivací nevyvozovali neexistenci limity podílu původních funkcí. Příkladem jsou funkce a pro . Pro ně platí , první člen jde k nule, ale druhý v blízkosti nuly osciluje mezi funkcí a . Proto neexistuje limita podílu derivací, ale původní limita je rovna nule, což plyne z toho, že pro každé leží v intervalu .
Příklad[editovat | editovat zdroj]
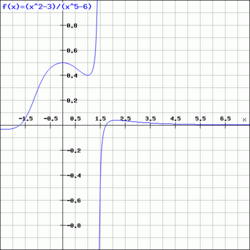
Určeme limitu , tj. a .
Všechny předpoklady kromě posledního jsou splněny. Poslední není na první pohled zřejmý, je nutno ověřit existenci limity podílu prvních derivací uvedených funkcí . Ověření provedeme opakovanou aplikací L'Hospitalova pravidla na limitu podílu prvních derivací uvedených funkcí , tj. limita podílu druhých derivací uvedených funkcí je pak . Z toho plyne, že jsou splněny předpoklady opakované aplikace L'Hospitalova pravidla, proto platí . Teprve z toho plyne, že můžeme L'Hospitalovo pravidlo použít i na náš původní příklad a platí .
Odkazy[editovat | editovat zdroj]
Reference[editovat | editovat zdroj]
- ↑ l’Hospital, Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes, strany 145–146
Literatura[editovat | editovat zdroj]
- BARTSCH, Hans-Jochen. Matematické vzorce. 4. vyd. Praha: Academia, 1994. 832 s. ISBN 80-200-1448-9.
Související články[editovat | editovat zdroj]
Externí odkazy[editovat | editovat zdroj]
 Obrázky, zvuky či videa k tématu L'Hospitalovo pravidlo na Wikimedia Commons
Obrázky, zvuky či videa k tématu L'Hospitalovo pravidlo na Wikimedia Commons - L'Hospitalovo pravidlo
































