Kyvadlo

Kyvadlo je těleso, volně otočné kolem pevné vodorovné osy, neprocházející jeho těžištěm. Pokud je takové těleso vychýleno z rovnovážné polohy, koná kývavý pohyb. Při něm se střídavě mění potenciální energie kyvadla na kinetickou energii kyvadla a naopak.

Této definici odpovídá fyzikální kyvadlo.

Příklad

Kyvadlo v ustáleném (vlevo) a kmitajícím stavu (vpravo).

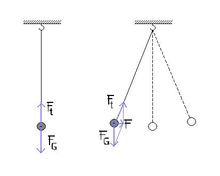
Příkladem kyvadla může být kulička zavěšená na tenkém provázku. Je to model mechanického oscilátoru. Volně zavěšená kulička je v rovnovážné poloze, kdy se tíhová síla $\mathbf{F}_G$ rovná tahové síle $\mathbf{F}_t$ závěsu. Pokud kyvadlo z rovnovážné polohy vychýlíme, vznikne složením sil $\mathbf{F}_G$ a $\mathbf{F}_t$ výslednice $\mathbf{F}$, která směřuje do rovnovážné polohy a vytváří tak kmitavý pohyb kyvadla. Po vychýlení se kyvadlo periodicky vrací do své rovnovážné polohy, kde má největší rychlost a pohybuje se dál, dokud nedosáhne největší výchylky, a pak se znovu vrací do rovnovážné polohy.

Matematické kyvadlo

Matematické kyvadlo je pak zvláštní případ, kdy je zkoumán pouze hmotný bod zavěšený na tenkém vláknu zanedbatelné hmotnosti. Perioda, tedy doba kmitu matematického kyvadla, je přímo úměrná druhé odmocnině z délky závěsu. Perioda kmitání kyvadla nezávisí na hmotnosti hmotného bodu.

Použití

• Kyvadlo a zákonitosti jeho pohybu umožnily konstrukci přesných hodin, které umožňovaly měřit čas mnohem přesněji než u předchozích modelů. Poprvé bylo použito v roce 1656.
• Kyvadlo se uplatnilo při konstrukci seismografu.
• Foucaultovo kyvadlo je kyvadlo umožňující experimentálně ověřit otáčení Země.

Související články

• Fyzikální kyvadlo
• Matematické kyvadlo
• Torzní kyvadlo
• Foucaultovo kyvadlo
• Balistické kyvadlo
• Kmitání
• Maxwellovo kyvadlo
• Kyvadlové hodiny