Petriho síť
Petriho síť je matematická reprezentace diskrétních distribuovaných systémů. Petriho síť graficky reprezentuje strukturu distribuovaného systému jako orientovaný bipartitní graf s ohodnocením. Taková Petriho síť má dva druhy uzlů označované jako místa a přechody a orientované hrany spojující místa s přechody. Petriho sítě byly vytvořeny roku 1962 Carlem Adamem Petrim v jeho disertační práci.
Základní Petriho sítě[editovat | editovat zdroj]
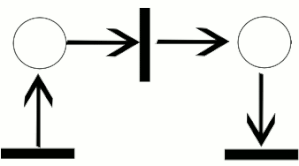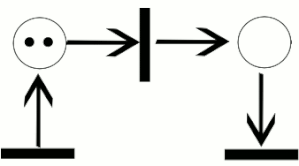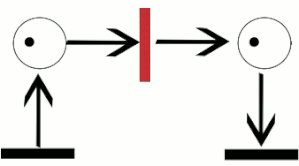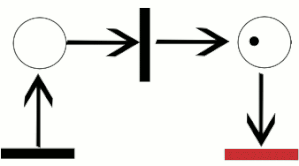
Petriho sítě obsahují místa, přechody a hrany. Hrany jsou pouze mezi místy a přechody, nikoliv mezi dvěma místy nebo dvěma přechody. Místa, ze kterých vedou hrany do přechodu, jsou nazývána vstupní místa tohoto přechodu; místa, do kterých vedou hrany z přechodu, jsou nazývána výstupní místa tohoto přechodu.
Místa mohou obsahovat libovolný počet teček (někdy též značek nebo tokenů; anglicky: tokens). Rozložení značek mezi místy v síti je nazýváno značení (anglicky: marking). Přechody mohou tečky ze vstupních míst takzvaně odpalovat (anglicky: firing) do míst výstupních. Přechod je uschopněn (anglicky: enabled) a může odpálit, pokud je v každém ze vstupních míst alespoň tečka. Když přechod odpálí, odebere tečky z jeho vstupních míst, provede nějaké výpočetní úlohy, a vloží zvolený počet teček do každého výstupního místa. Tento proces činí automaticky v každém jednotlivém kroku.
Výpočet Petriho sítě je nedeterministický. Což znamená následující:
- více přechodů může být uschopněno současně a libovolný může odpálit,
- žádný přechod není nutno odpálit – odpalují se dle libosti mezi časy 0 až nekonečno nebo vůbec nikdy. Je tedy možné, že se neodpálí vůbec nic.
Protože je odpalování nedeterministické, Petriho sítě jsou vhodné pro modelování souběžného chování distribuovaných systémů.
Formální definice[editovat | editovat zdroj]
Petriho síť je pětice , kde (viz Desel a Juhás[1])
- je konečná množina míst.
- je konečná množina přechodů.
- je konečná množina hran, kde žádná hrana nemůže spojovat dvě místa nebo dva přechody, formálněji: .
- je počáteční označkování, kde v každém místě je teček.
- je množina vážených hran, které přiřazuje každé hraně nějaké číslo označující kolik teček je odebráno z místa tímto přechodem, nebo alternativně: kolik teček je přechodem produkováno a vloženo do každého výstupního místa.
Existuje mnoho variant formálních definic – některé nemají vážené hrany, ale povolují více hran mezi stejným místem a přechodem, což je koncepčně shodné s jednou hranou s váhou rovnou počtu těchto hran z původní definice.
Odkazy[editovat | editovat zdroj]
Reference[editovat | editovat zdroj]
- ↑ Desel, Jörg a Juhás, Gabriel „What Is a Petri Net? – Informal Answers for the Informed Reader“, Hartmut Ehrig et al. (Eds.): Unifying Petri Nets, LNCS 2128, pp. 1-25, 2001. [1][nedostupný zdroj]
Související články[editovat | editovat zdroj]
Externí odkazy[editovat | editovat zdroj]
 Obrázky, zvuky či videa k tématu Petriho síť na Wikimedia Commons
Obrázky, zvuky či videa k tématu Petriho síť na Wikimedia Commons - Svět Petriho sítí – anglicky
- Citace v CiteSeeru – anglicky











